When the SAS Global Forum 2020 conference was cancelled by the global COVID-19 pandemic, I felt sorry for the customers and colleagues who had spent months preparing their presentations. One presentation I especially wanted to attend was by Bucky Ransdell and Randy Tobias: "Introducing PROC SIMSYSTEM for Systematic Nonnormal Simulation".
A previous article shows a simulation of two different models of a foraging animal. The first model is a random walk, which assumes that the animal chooses a random direction, then takes a step that is distributed according to a Gaussian random variable. In the second model, the animal again
A remarkable result in probability theory is the "three-sigma rule," which is a generic name for theorems that bound the probability that a univariate random variable will appear near the center of its distribution. This article discusses the familiar three-sigma rule for the normal distribution, a less-familiar rule for unimodal
This article shows how to simulate data from a Poisson regression model, including how to account for an offset variable. If you are not familiar with how to run a Poisson regression in SAS, see the article "Poisson regression in SAS." A Poisson regression model is a specific type of
An article published in Nature has the intriguing title, "AI models collapse when trained on recursively generated data." (Shumailov, et al., 2024). The article is quite readable, but I also recommend a less technical overview of the result: "AI models fed AI-generated data quickly spew nonsense" (Gibney, 2024). The Gibney
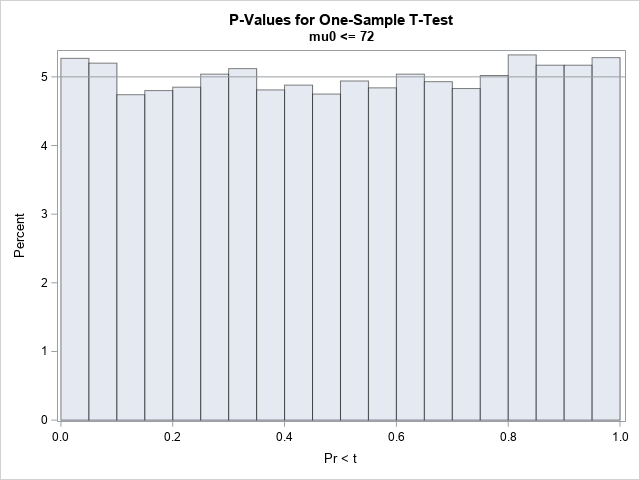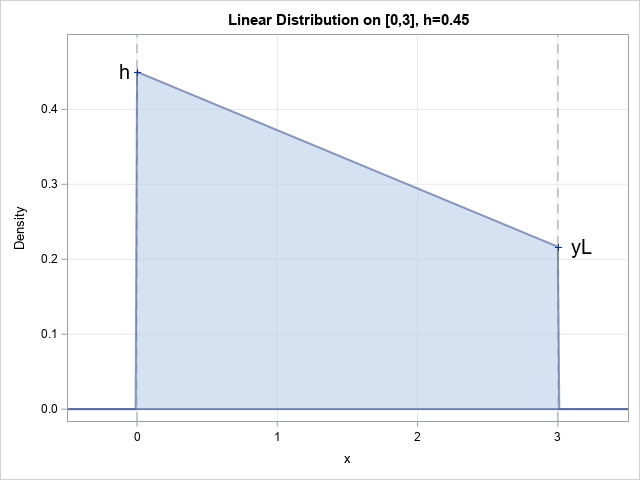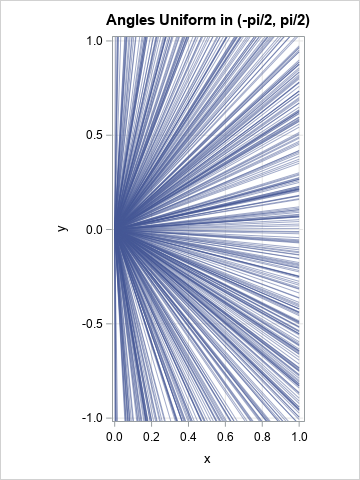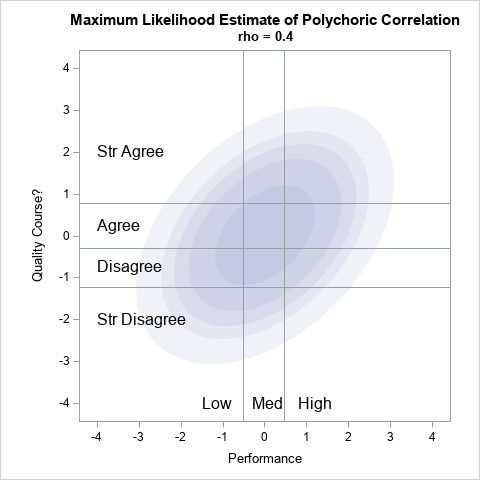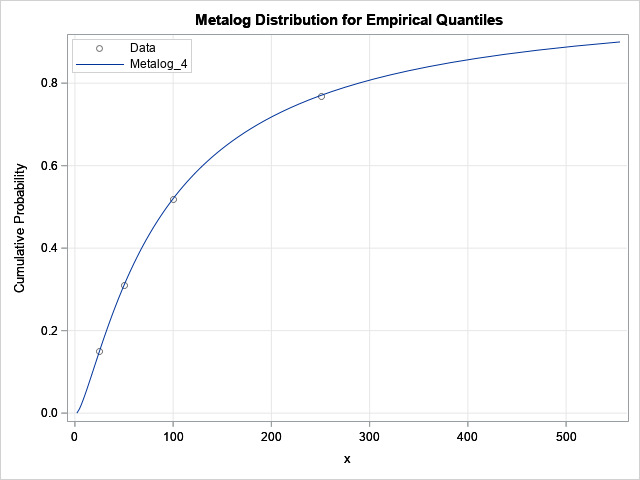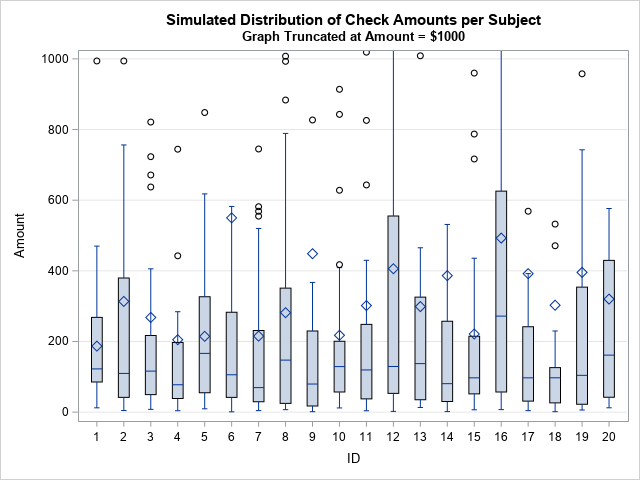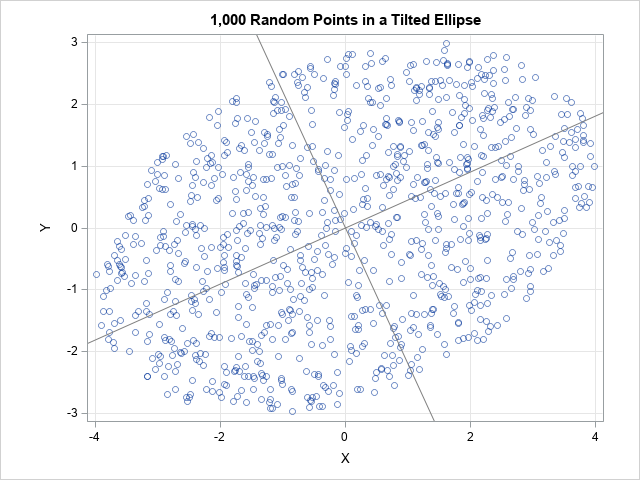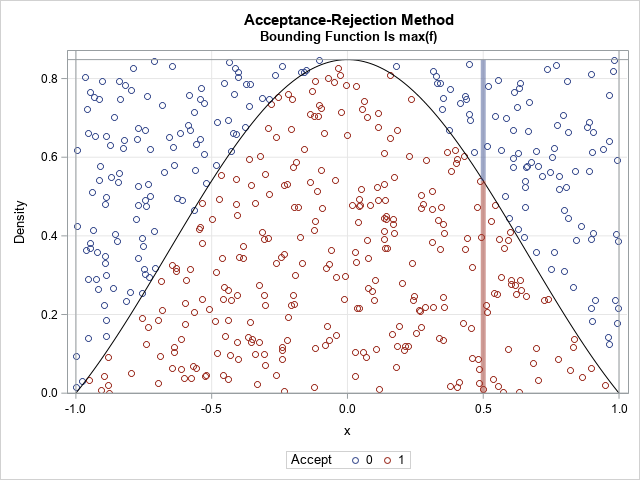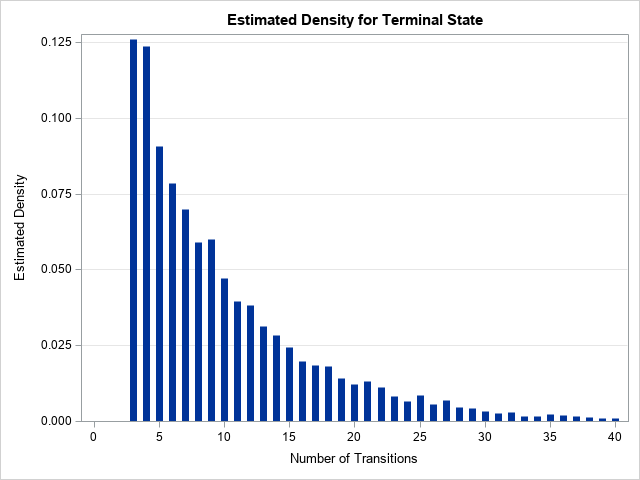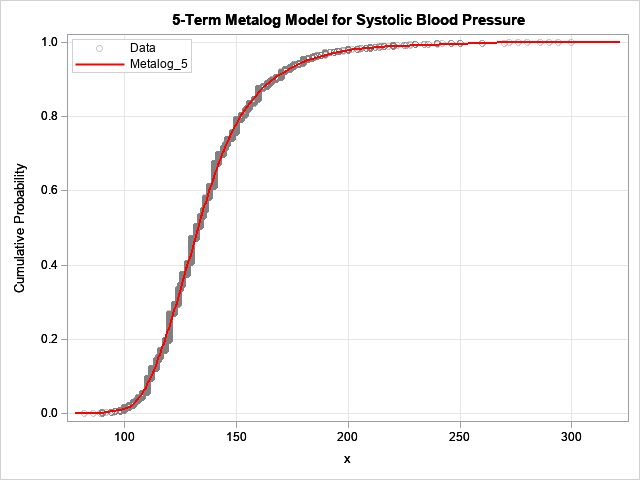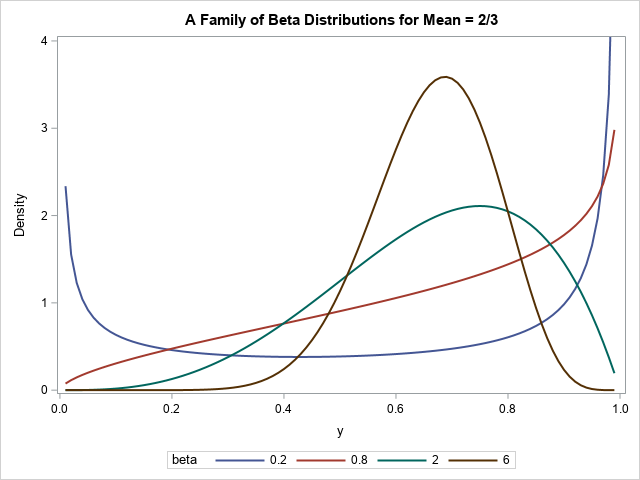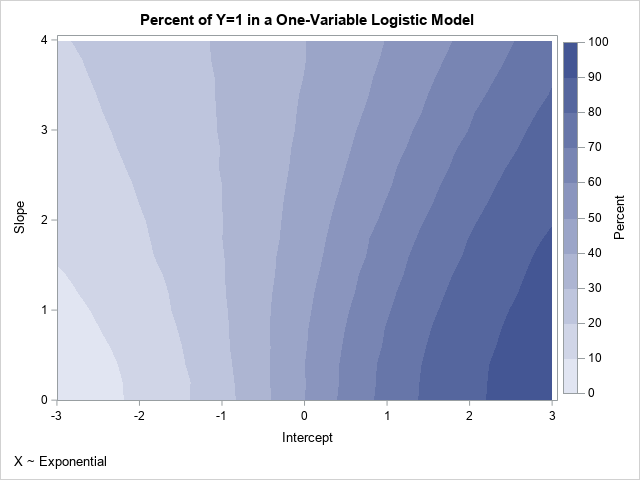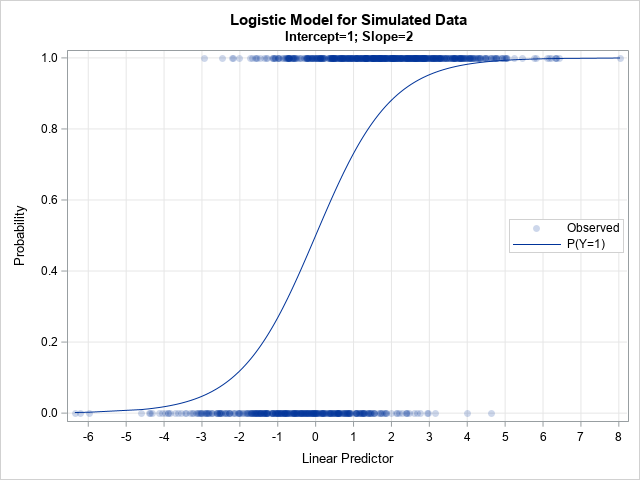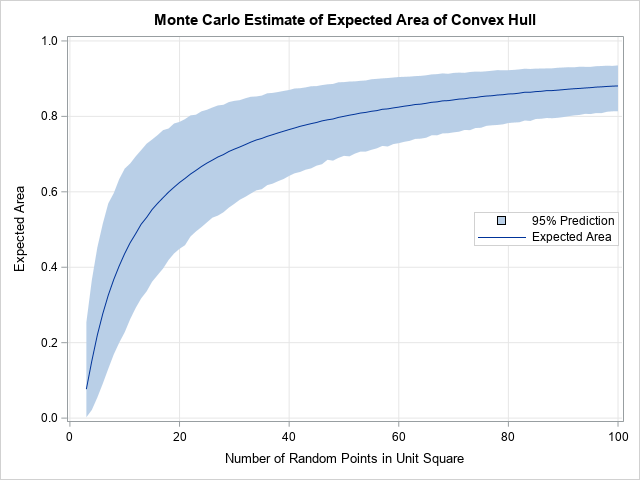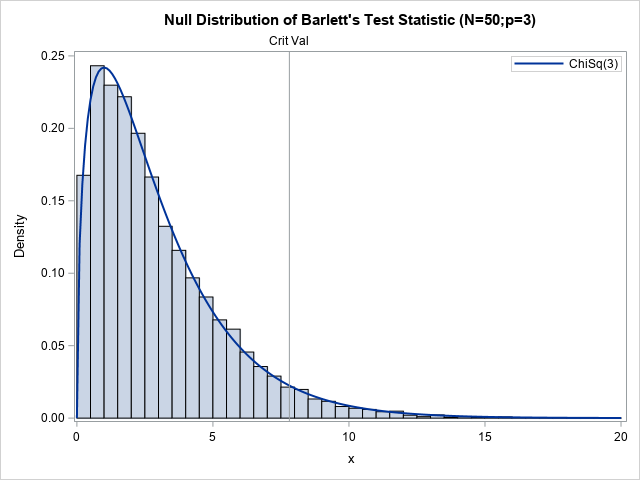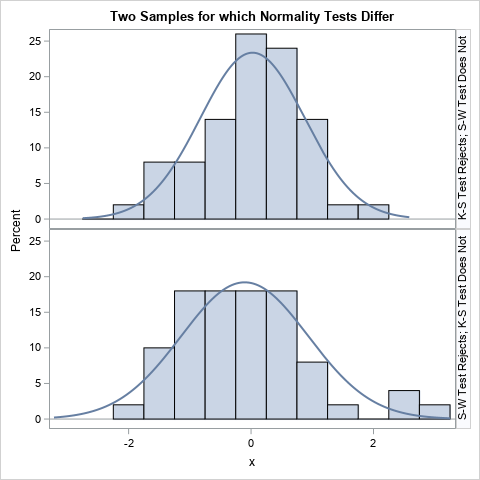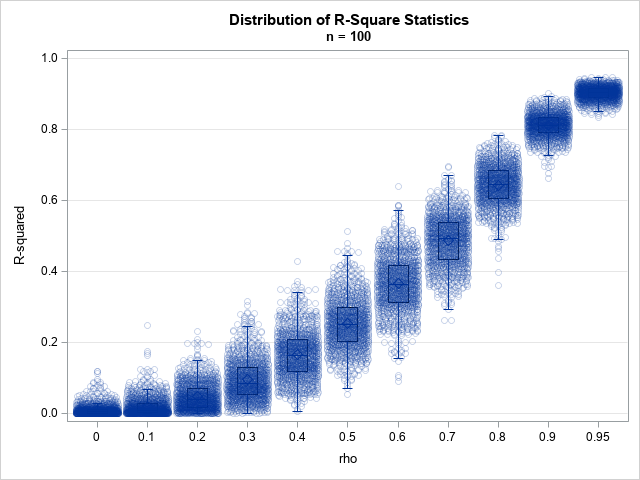
A SAS analyst ran a linear regression model and obtained an R-square statistic for the fit. However, he wanted a confidence interval, so he posted a question to a discussion forum asking how to obtain a confidence interval for the R-square parameter. Someone suggested a formula from a textbook (Cohen,
After writing a program that simulates data, it is important to check that the statistical properties of the simulated (synthetic) data match the properties of the model. As a first step, you can generate a large random sample from the model distribution and compare the sample statistics to the expected
A SAS statistical programmer recently asked a theoretical question about statistics. "I've read that 'p-values are uniformly distributed under the null hypothesis,'" he began, "but what does that mean in practice? Is it important?" I think data simulation is a great way to discuss the conditions for which p-values are
In a recent Monte Carlo project, I needed to simulate numbers on an interval by using a continuous linear probability density function (PDF). An example is shown to the right. In this example, the linear density function is decreasing on the interval, but the function could also be constant or
There are two popular ways to express the steepness of a line or ray. The most-often used mathematical definition is from high-school math where the slope is defined as "rise over run." A second way is to report the angle of inclination to the horizontal, as introduced in basic trigonometry.
Statistical software provides methods to simulate independent random variates from continuous and discrete distributions. For example, in the SAS DATA step, you can use the RAND function to simulate variates from continuous distributions (such as the normal or lognormal distributions) or from discrete distributions (such as the Bernoulli or Poisson).
The world’s largest rugby tournament returns for the knockout stages. This blog post explores how probability and simulation can be used to predict likely winners in each of the knockout stages. Team sports are dynamic, time-varying and complex topics to model. When modeling regular competitions, such as domestic leagues, it
There are many ways to model a set of raw data by using a continuous probability distribution. It can be challenging, however, to choose the distribution that best models the data. Are the data normal? Lognormal? Is there a theoretical reason to prefer one distribution over another? The SAS has
Does anyone write paper checks anymore? According to researchers at the Federal Reserve Bank of Atlanta (Greene, et al., 2020), the use of paper checks has declined 63% among US consumers since the year 2000. The researchers surveyed more than 3,000 consumers in 2017-2018 and discovered that only 7% of
I have previously written about how to efficiently generate points uniformly at random inside a sphere (often called a ball by mathematicians). The method uses a mathematical fact from multivariate statistics: If X is drawn from the uncorrelated multivariate normal distribution in dimensiond, then S = r*X / ||X|| has
The acceptance-rejection method (sometimes called rejection sampling) is a method that enables you to generate a random sample from an arbitrary distribution by using only the probability density function (PDF). This is in contrast to the inverse CDF method, which uses the cumulative distribution function (CDF) to generate a random
A previous article shows an example of a Markov chain model and computes the probability that the system ends up in a terminal state (called an absorbing state). As explained previously, you can often compute exact probabilities for questions about Markov chains. Nevertheless, it can be useful to know how
The "Teacher’s Corner" of The American Statistician enables statisticians to discuss topics that are relevant to teaching and learning statistics. Sometimes, the articles have practical relevance, too. Andersson (2023) "The Wald Confidence Interval for a Binomial p as an Illuminating 'Bad' Example," is intended for professors and masters-level students in
A previous article describes the metalog distribution (Keelin, 2016). The metalog distribution is a flexible family of distributions that can model a wide range of shapes for data distributions. The metalog system can model bounded, semibounded, and unbounded continuous distributions. This article shows how to use the metalog distribution in
A SAS programmer asked for help to simulate data from a distribution that has certain properties. The distribution must be supported on the interval [a, b] and have a specified mean, μ, where a < μ < b. It turns out that there are infinitely many distributions that satisfy these
SAS programmers love to make special graphs for Valentine's Day. In fact, there is a long history of heart-shaped graphs and love-inspired programs written in SAS! Last year, I added to the collection by showing how a ball bounces on a heart-shaped billiards table. This year, I create a similar
A previous article shows that you can use the Intercept parameter to control the ratio of events to nonevents in a simulation of data from a logistic regression model. If you decrease the intercept parameter, the probability of the event decreases; if you increase the intercept parameter, the probability of
This article shows that you can use the intercept parameter to control the probability of the event in a simulation study that involves a binary logistic regression model. For simplicity, I will simulate data from a logistic regression model that involves only one explanatory variable, but the main idea applies
SAS' Bahar Biller expounds on the idea that stochastic simulations are large-data generation programs for highly complex and dynamic stochastic systems.
A probabilistic card trick is a trick that succeeds with high probability and does not require any skill from the person performing the trick. I have seen a certain trick mentioned several times on social media. I call it "ladders" or the "ladders game" because it reminds me of the
A SAS programmer was trying to simulate poker hands. He was having difficulty because the sampling scheme for simulating card games requires that you sample without replacement for each hand. In statistics, this is called "simple random sampling." If done properly, it is straightforward to simulate poker hands in SAS.
I recently blogged about how to compute the area of the convex hull of a set of planar points. This article discusses the expected value of the area of the convex hull for n random uniform points in the unit square. The article introduces an exact formula (due to Buchta,
One of the benefits of social media is the opportunity to learn new things. Recently, I saw a post on Twitter that intrigued me. The tweet said that the expected volume of a random tetrahedron in the unit cube (in 3-D) is E[Volume] = 0.0138427757.... This number seems surprisingly small!
A common question on SAS discussion forums is how to use SAS to generate random ID values. The use case is to generate a set of random strings to assign to patients in a clinical study. If you assign each patient a unique ID and delete the patients' names, you
When I was writing Simulating Data with SAS (Wicklin, 2013), I read a lot of introductory textbooks about Monte Carlo simulation. One of my favorites is Sheldon Ross's book Simulation. (I read the 4th Edition (2006); the 5th Edition was published in 2013.) I love that the book brings together
