Simulate poker hands in SAS

A SAS programmer was trying to simulate poker hands. He was having difficulty because the sampling scheme for simulating card games requires that you sample without replacement for each hand. In statistics, this is called "simple random sampling."

If done properly, it is straightforward to simulate poker hands in SAS. This article shows how to generate a standard deck of 52 cards. It then shows how to generate many card hands for a game that involves several players. This can be done in two ways: The SAMPLE function in the SAS/IML language and PROC SURVEYSELECT in SAS/STAT software.

Encode a deck of cards

The first step is to generate a standard deck of 52 playing cards. There are many ways to do this, but the following DATA step iterates over 13 values (A, 2, 3, ..., Q, K) and over four suits (clubs, diamonds, hearts, and spades). The step creates a data set that has 52 cards. To make the output more compact, I concatenate the value of the card with the first letter of the suit to obtain a two-character string for each card. For example, "5C" is the "five of clubs" and "AS" is the "ace of spades." So that each card can be represented by using two characters, I use "T" instead of "10." For example, "TH" is the "ten of hearts." The

data Cards;
length Value $2 Suit $8 Card $3;
array Values[13] $ _temporary_ ('A','2','3','4','5','6','7','8','9','T','J','Q','K');
array Suits[4] $ _temporary_ ('Clubs', 'Diamonds', 'Hearts', 'Spades');
do v = 1 to 13;
   do s = 1 to 4;
      Value = Values[v]; Suit = Suits[s]; Card = cats(Value,substr(Suit,1,1));
      output;
   end;
end;
run;
 
proc print data=Cards(obs=8); 
   var v s Value Suit Card;
run;

The cards are generated in order. The output shows the first eight cards in the deck, which are the aces and twos. For some types of poker hands (such as determining pairs and straights), the V variable can be useful, and for other analyses (such as determining flushes), the S variable can be useful.

Deal cards by using SAS/IML

When humans deal cards, we use a two-step method: shuffle the deck and then deal the top cards to players in a round-robin fashion. A computer simulation can simluate dealing cards by using a one-step method: deal random cards (without replacement) to every player. SAS provides built-in sampling methods to make this process easy to program.

In SAS/IML, the default sampling method for the SAMPLE function is sampling without replacement. If there are P players and each player is to receive C cards, then a deal consists of P*C cards, drawn without replacement from the deck. The deck does not need to be shuffled because the SAMPLE function outputs the cards in random order. Because the cards are in random order, it does not matter how you assign the cards to the players. The following SAS/IML program uses P=3 players and generates C=5 cards for each player. The program simulates one deal by assigning the first C cards to the first player, the second C cards to the second player, and so on:

%let nCards   = 5;    /* cards per player */
%let nPlayers = 3;    /* number of players */
%let nDeals   = 10;   /* number of deals to simulate */
 
/* simulate dealing many card hands in SAS/IML */
proc iml;
call randseed(1234);                       /* set random number seed */
use Cards;  read all var "Card";  close;   /* read the deck of cards into a vector */
 
nCardsPerDeal = &nCards * &nPlayers;       /* each row is a complete deal */
D = sample(Card, nCardsPerDeal, "WOR" );   /* sample without replacement from the deck */
Deal = shape(D, &nPlayers, &nCards);       /* reshape into nPlayers x nCards matrix */
 
/* print one deal */
cardNames   = "C1":"C&nCards";
playerNames = "P1":"P&nPlayers";
print Deal[c=cardNames r=playerNames];

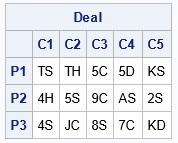
For this deal, the first player has two tens, two fives, and a king. The second player has a four, a five, a nine, an ace, and a two. You could sort the cards in each row, but I have left each player's cards unsorted so that you can see the random nature of the assignment.

Simulate multiple deals

The previous program simulates one deal. What if you want to simulate multiple deals? One way is to loop over the number of deals, but there is a more efficient method. The second argument to the SAMPLE function can be a two-element vector. The first element specifies the number of cards for each deal, and the second element specifies the number of deals. Thus, for example, if you want to simulate 10 deals, you can use the following statement to generate a matrix that has 10 rows. Each row is a sample (without replacement) from a 52-card deck:

/* use one call to simulate many deals */
D = sample(Card, nCardsPerDeal//&nDeals, "WOR" );   /* simulate many deals */
 
/* Ex: The 8th row contains the 8th deal. Display it. */
Deal8 = shape(D[8,], &nPlayers, &nCards);
print Deal8[c=cardNames r=playerNames];

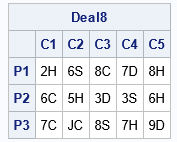
To demonstrate that each row is a deal, I have extracted, reshaped, and displayed the eighth row. The eighth deal is unusual because each player is dealt a "good" hand. The first player has a pair of eights, the second player has two pairs (threes and sixes), and the third player has a pair of sevens. If you want to print (or analyze) the 10 deals, you can loop over the rows, as follows:

do i = 1 to &nDeals;
   Deal = shape(D[i,], &nPlayers, &nCards);
   /* analyze or print the i_th deal */
   print i, Deal[c=cardNames r=playerNames];
end;

Deal random hands by using PROC SURVEYSELECT

You can also simulate card deals by using the SURVEYSELECT procedure. You should use the following options:

Use the METHOD=SRS option to specify sampling without replacement for each deal. To obtain the cards in random order, use the OUTRANDOM option.
Use the N= option to specify the number of cards in each deal.
Use the REPS= option to specify the total number of deals.

An example is shown in the following call to PROC SURVEYSELECT:

/* similar approach for PROC SURVEYSELECT */
proc surveyselect data=Cards seed=123 NOPRINT
     method=SRS                   /* sample without replacement */
     outrandom                    /* randomize the order of the cards */
     N=%eval(&nCards * &nPlayers) /* num cards per deal */
     reps=&nDeals                 /* total number of deals */
     out=AllCards;
run;

The output data set (AllCards) contains a variable named Replicate, which identifies the cards in each deal. Because the cards for each deal are in a random order, you can arbitrarily assign the cards to players. You can use a round-robin method or assign the first C cards to the first player, the next C cards to the second player, and so on. This is done by using the following DATA step:

/* assign the cards to players */
data AllDeals;
set AllCards;
by Replicate;
if first.Replicate then do;
   Cnt = 0;
end;
Player = 1 + floor(Cnt/&nCards);
Cnt + 1;
drop Cnt;
run;

The simulated data are in long form. For some analyses, it might be more convenient to convert it into wide form. You can do this by using the DATA step or by using PROC TRANSPOSE, as below:

/* OPTIONAL: Convert from long form to wide form */
proc transpose data=AllDeals 
               out=Deals(rename=(col1-col&nCards=C1-C&nCards) drop=_NAME_);
   var Card;
   by Replicate Player;
run;
 
proc print data=Deals;
   where Replicate=8;
   var Replicate Player C:;
run;

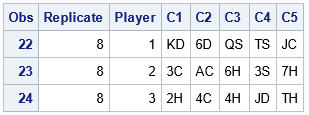
To demonstrate the results, I display the result of the eighth deal (Replicate=8). For this deal, the first player has several face cards but no pairs, the second player has a pair of threes, and the third player has a pair of fours.

Summary

SAS provides many tools for simulation studies. For simulations of card games, this article shows how to create a data set that represents a standard deck of 52 playing cards. From the cards, you can use the SAMPLE function in SAS/IML software or the SURVEYSELECT procedure to simulate many deals, where each deal is a sample without replacement from the deck. For each deal, you can assign the cards to the players in a systematic manner.

Blogs