Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
The article "Order two-dimensional vectors by using angles" shows how to re-order a set of 2-D vectors by their angles. Because angles are on a circle, which has no beginning and no end, you must specify which vector will appear first in the list. The previous article finds the largest
Order matters. The order of variables in tables and rows of a correlation matrix can make a big difference in how easy it is to observed correlations between variables or groups of variables. There are many ways to order the variables, but this article shows how to display the variables
In a correlation analysis, it is common to consider the correlations between all pairs of numerical variables. That is, if there are k numerical variables, most people examine the complete k x k matrix of correlations. This matrix is symmetric and has 1s on the diagonal, so more than half of the
A previous article discusses the MakeString function, which you can use to convert an IML character vector into a string. This can be very useful. When I originally wrote the MakeString function, I was disappointed that I could not vectorize the computation. Recently, I learned about the COMBL function in
When the SAS Global Forum 2020 conference was cancelled by the global COVID-19 pandemic, I felt sorry for the customers and colleagues who had spent months preparing their presentations. One presentation I especially wanted to attend was by Bucky Ransdell and Randy Tobias: "Introducing PROC SIMSYSTEM for Systematic Nonnormal Simulation".
A previous article shows a simulation of two different models of a foraging animal. The first model is a random walk, which assumes that the animal chooses a random direction, then takes a step that is distributed according to a Gaussian random variable. In the second model, the animal again
In SAS, range attribute maps enable you to specify the range of values that determine the colors used for graphical elements. There are various examples that use the GTL to define a range attribute map, but fewer examples that show how to use a range attribute map with PROC SGPLOT.
A common way to visualize the sample correlations between many numeric variables is to display a heat map that shows the Pearson correlation for each pair of variables, as shown in the image to the right. The correlation is a number in the range [-1, 1], where -1 indicated perfect
The INPUT function and PUT function in SAS are used to apply informats and formats (respectively) to data. For both functions, you must know in advance which informat or format you want to apply. For brevity, let's consider only applying a format. To use the PUT function, you must know
In SAS, the INPUT and PUT functions are powerful functions that enable you to convert data from character type to numeric type and vice versa. They work by applying SAS formats or informats to data. You cannot fully understand the INPUT and PUT functions without understanding formats and informats in
SAS software supports two kinds of procedures: interactive and non-interactive. Most SAS procedures are non-interactive. They begin with a PROC statement, include one or more additional statements, and end with a RUN statement. When SAS encounters the RUN statement, the procedure executes all statements, then exits. On the other hand,
A remarkable result in probability theory is the "three-sigma rule," which is a generic name for theorems that bound the probability that a univariate random variable will appear near the center of its distribution. This article discusses the familiar three-sigma rule for the normal distribution, a less-familiar rule for unimodal
In practice, there is no need to remember textbook formulas for the ANOVA test because all modern statistical software will perform the test for you. In SAS, the ANOVA procedure is designed to handle balanced designs (the same number of observations in each group) whereas the GLM procedure can handle
A previous article about how to display missing values in SAS prompted a comment about special missing values in ODS tables in SAS. Did you know that statistical tables in SAS include special missing values to represent certain situations in statistical analyses? This article explains how to interpret four special
In statistical tables in SAS, a dot (.) represents a numerical missing value. Although a dot is the default symbol in SAS, other languages use other symbols. The R language prints the symbol NA, which stands for "not available." The MATLAB language uses NaN ("Not a Number"). In Python, many
Modern software for statistical graphics automatically handles many details and graph defaults, such as the range of the axes and the placement of tick marks. In the days of yore, these details required tedious manual calculations. Think about what is required to place ticks on a scatter plot. On the
In SAS, DATA step programmers use the IN operator to determine whether a value is contained in a set of target values. Did you know that there is a similar functionality in the SAS IML language? The ELEMENT function in the SAS IML language is similar to the IN operator
A previous article shows how to implement recursive formulas in SAS. The article points out that you can often avoid recursion by using an iterative algorithm, which is more efficient. An example is the Fibonacci sequence, which is usually defined recursively as F(n) = F(n-1) + F(n-2) for n
Many well-known distributions become more and more "normal looking" for large values of a parameter. Famously, the binomial distribution, Binom(p, N), can be approximated by a normal distribution when N (the sample size) is large. Similarly, the Poisson(λ) distribution is well approximated by the normal distribution when λ is large.
There are two programming tools that I rarely use: the SAS macro language and recursion. The SAS macro language is a tool that enables you to generate SAS statements. I rarely use the SAS macro language because the SAS IML language supports all the functionality required to write complex programs,
The SAS IML Language has a quirk with regards to functions that take no arguments. As discussed in the documentation, "modules with arguments are given a local symbol table." This is the usual behavior that programmers expect. However, the documentation goes on to state that "a module that has no
In SAS, the easiest way to draw random sampling from data is to use PROC SURVEYSELECT or the SAMPLE function in SAS IML software. I have previously written about how to implement four common sampling schemes by using PROC SURVEYSELECT and the SAMPLE function. The DATA step in SAS is
This article shows how to simulate data from a Poisson regression model, including how to account for an offset variable. If you are not familiar with how to run a Poisson regression in SAS, see the article "Poisson regression in SAS." A Poisson regression model is a specific type of
This article demonstrates how to use PROC GENMOD to perform a Poisson regression in SAS. There are different examples in the SAS documentation and in conference papers, but I chose this example because it uses two categorical explanatory variables. Therefore, the Poisson regression can be visualized by using a contingency
An article published in Nature has the intriguing title, "AI models collapse when trained on recursively generated data." (Shumailov, et al., 2024). The article is quite readable, but I also recommend a less technical overview of the result: "AI models fed AI-generated data quickly spew nonsense" (Gibney, 2024). The Gibney
A previous article shows that you can run a simple (one-variable) isotonic regression by using a quadratic programming (QP) formulation. While I was reading a book about computational geometry, I learned that there is a connection between isotonic regression and the convex hull of a certain set of points. Whaaaaat?
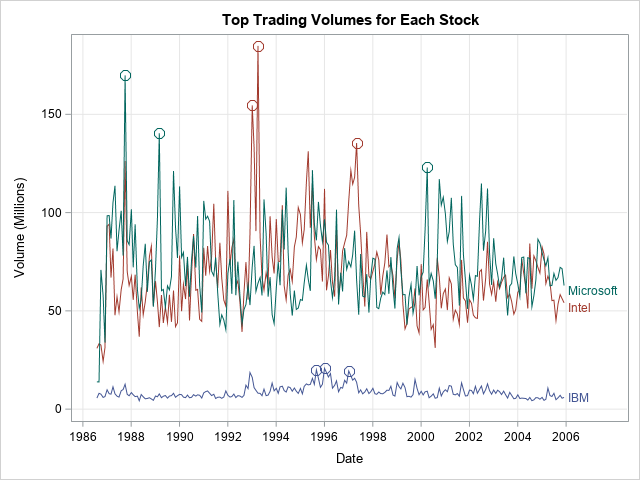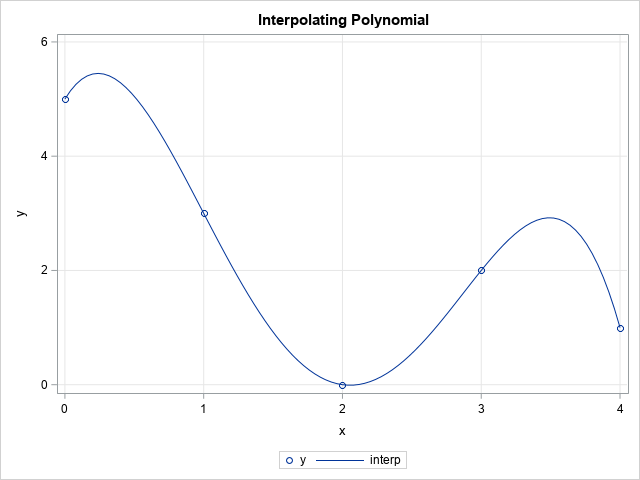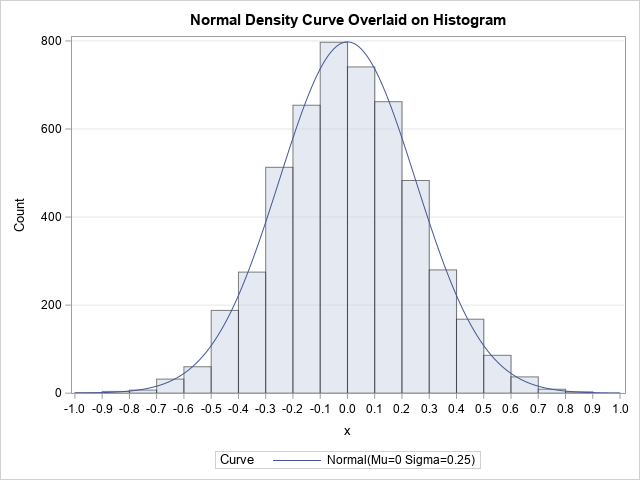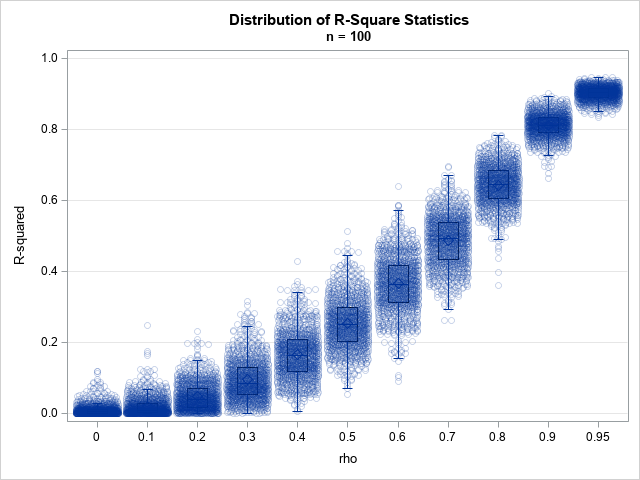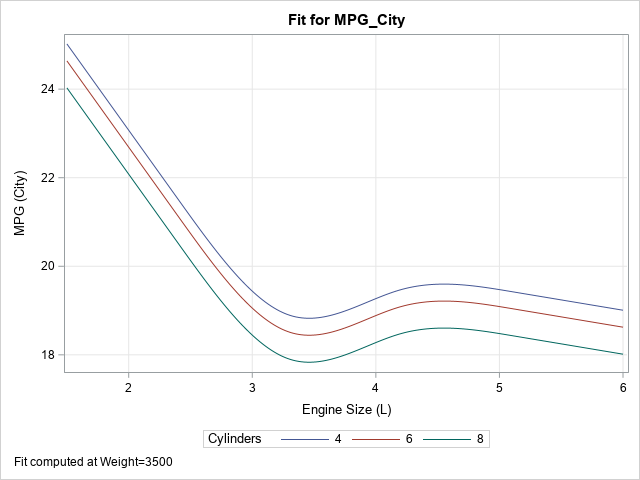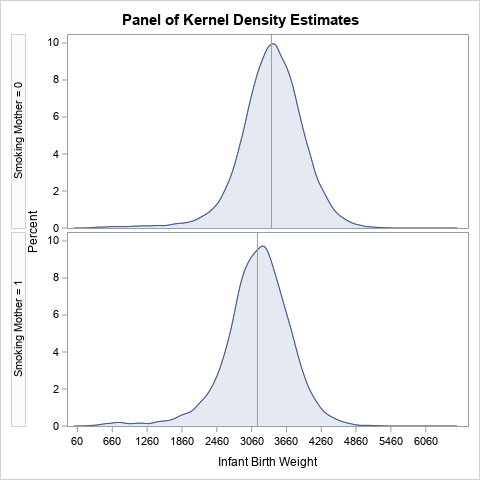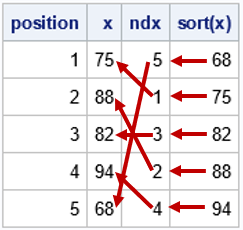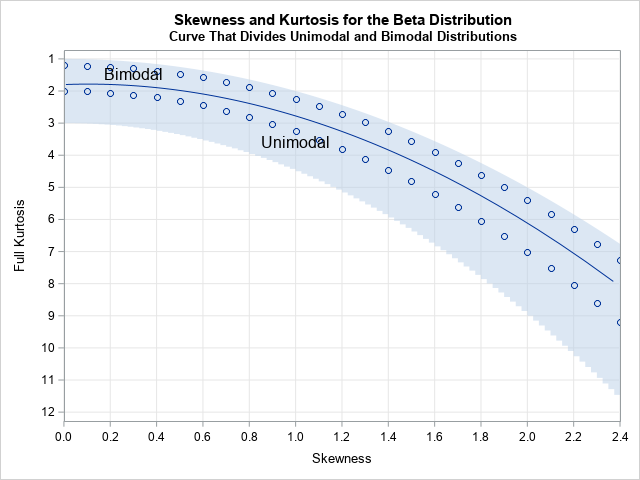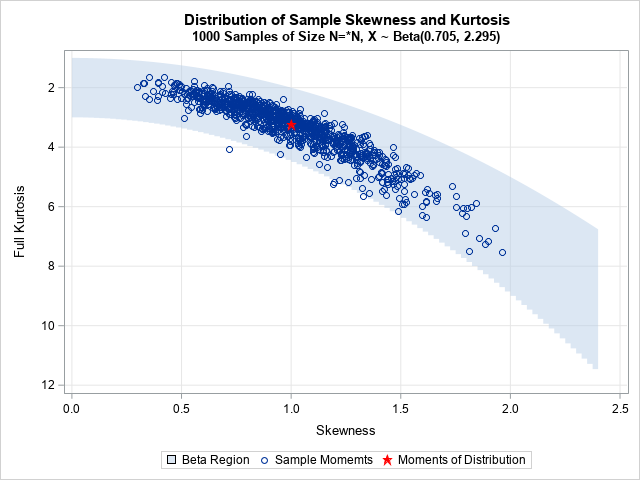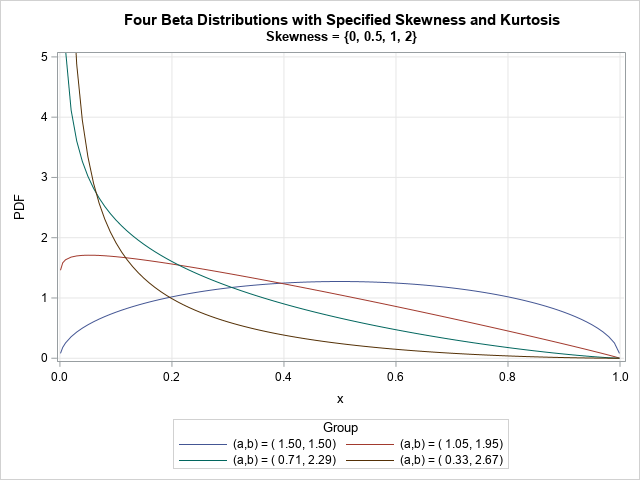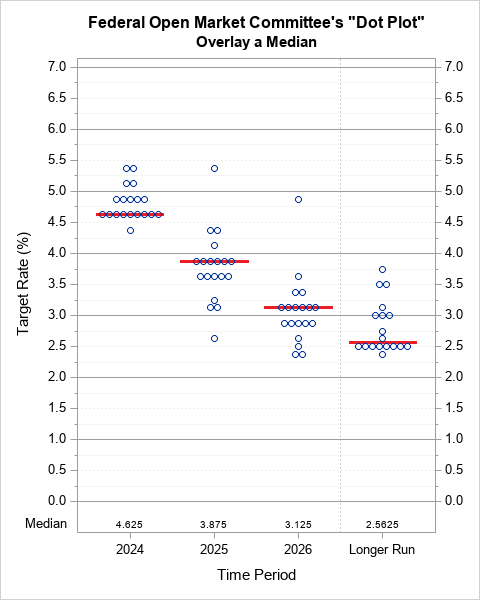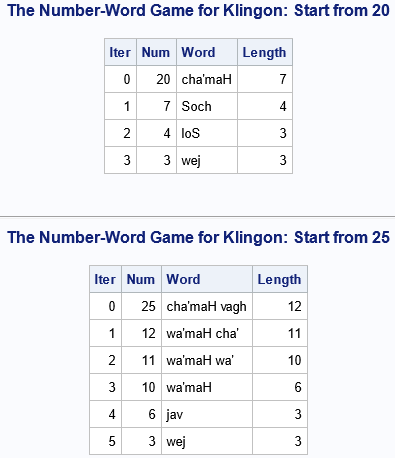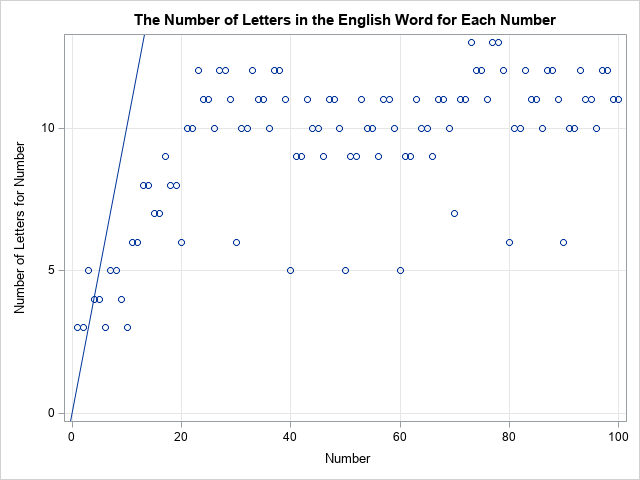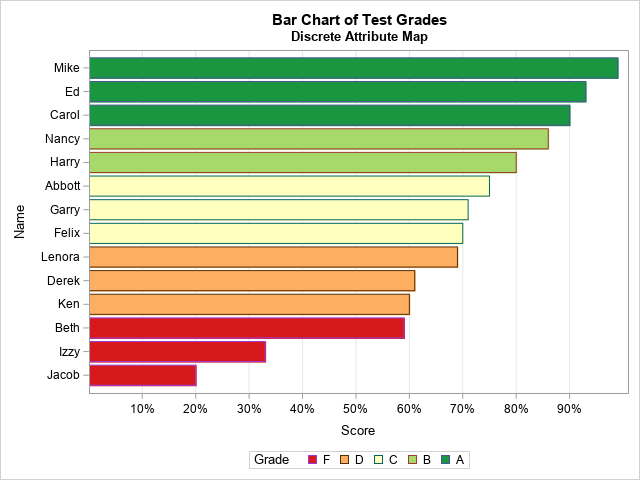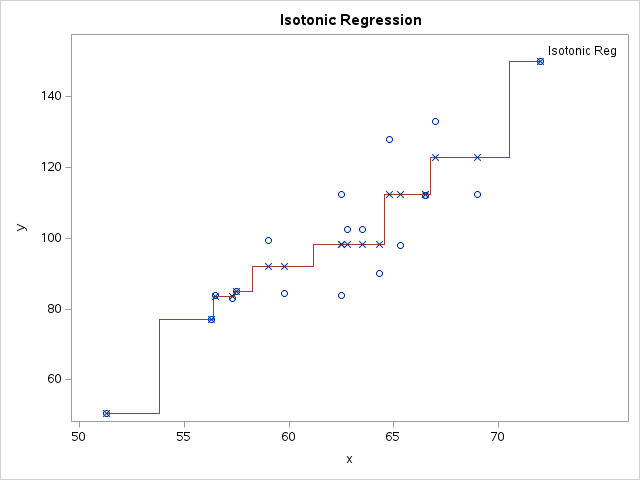
Since the pandemic began in 2020, the SAS IML developers have added about 50 new functions and enhancements to the SAS IML language in SAS Viya. Among these functions are new modern methods for optimization that have a simplified syntax as compared to the older 'NLP' functions that are available
Just like the SAS DATA step, the SAS IML language supports both functions and subroutines. A function returns a value, so the calling syntax is familiar: y = func(x1, x2); /* the function returns one value, y */ In this syntax, the input arguments are x1 and x2. The
Isotonic regression (also called monotonic regression) is a type of regression model that assumes that the response variable is a monotonic function of the explanatory variable(s). The model can be nondecreasing or nonincreasing. Certain physical and biological processes can be analyzed by using an isotonic regression model. For example, a
A previous article discusses the fact that there are often multiple ways in SAS to obtain the same result. This fact results in many vigorous discussions on online programming forums as people propose different (but equivalent) methods for solving someone's problem then argue why their preferred method is better than
