I recently wrote about the Number-Word Game, which is an iterative algorithm that generates a sequence of natural numbers by using the lengths of the words for the numbers. In English, the words are "one", "two", "three", and so on. You can play the Number-Word Game in any alphabetic language (Spanish, French, German), but the game is not interesting for ideographic languages (such as Chinese or Japanese) that use a single character to represent entire words.

If you know how to write the words for each natural number in a language, you can play the Number-Word Game:

1. Start with any natural number.
2. Write down the word(s) for the integer in the chosen language.
3. Count the number of characters in the word. This gives a new natural number.
4. Go to (2). Repeat until a portion of the sequence repeats itself, at which point the game ends.

In the previous article, I wrote a SAS program that plays the Number-Word Game in English. I showed that every sequence of integers terminates at the number 4, which is a fixed point for the English game. However, if you use other languages, you can get multiple fixed points or periodic cycles.

This article creates a SAS macro that enables you to play the Number-Word game in any alphabetic language. I demonstrate the program for Spanish and show that some sequences converge to a fixed point whereas others converge to a period-two cycle. Then, I play the game in Klingon, a fictional language from the Star Trek universe. (Qa'Pla. NuqneH, nuqDaq ‘oH puchpa’‘e’?, which means "Welcome. Where are you from, fellow Klingon?")

A SAS program to play the Number-Word Game

Let's start by writing a SAS program to play the Number-Word Game. The following macro contains a DATA step and a PROC PRINT statement. It is based on the program in the previous article, but it has a few differences:

• The macro takes two arguments.
• The first argument is the name of a SAS data set. I suggest you name the data set after the language: Spanish, French, Klingon, etc. The data set must contain k character variables with the names W1-Wk. The value of Wi is the character representation of the number i in the selected language. For example, in English, the variables W1, W2, and W3 contain the values "one", "two" and "three", respectively. In Spanish, the variables W1, W2, and W3 contain the values "uno", "dos" and "tres".
• The second argument is a natural number (less than k) to use as the initial number in the game.
• The program uses the KLENGTH function, which is the preferred function for counting the number of characters in a non-English string.
• The program stops iterating if it encounters a fixed point or a period-two cycle. You could augment the program to detect cycles of higher periods.
• The program can only analyze numbers 1-k; My examples use k=30.

%macro NumberWordGame(Language, N0);
options nonotes;
   data IterHistory;
   keep Iter Num Word Length;
   set &Language;
   array W[*] W:;  /* W1-W&MaxN */
   length Word $100;
 
   Iter = 0; PrevNum = .; Num = &N0; 
   if Num > dim(W) then do;
      put "ERROR: Invalid input: " Num;
      STOP;
   end;
   Word = W[Num]; Length = klength(Word); 
   output;
   stopCond = (Length=Num | Length=PrevNum);
   /* stop if reach fixed point or period-two cycle */
   do Iter=1 to 20 while (^stopCond);  
      PrevNum = Num;
      Num = Length;
      if Num > dim(W) then do;
         put "ERROR: Invalid value: " Num;
         STOP;
      end;
      Word = W[Num];
      Length = klength(Word);  /* will become the next Num */
      stopCond = (Length=Num | Length=PrevNum);
      output;
   end;
   run;
 
   title "The Number-Word Game for &Language: Start from &N0";
   proc print data=IterHistory noobs;
      var Iter Num Word Length;
   run;
options notes;
%MEND;

The next section shows how to define the input data set for the Spanish language.

The Number-Word Game in Spanish

The following SAS DATA step defines a data set that has 30 character variables named W1-W30. The contents of the data set are the Spanish words "uno", "dos", "tres", ..., "veintinueve", and "treinta". You can type these values directly on the ARRAY statement, or read the values from data lines, as follows:

/* Read the Spanish numbers 1-30 into arrays */
%let MaxN = 30;
data Spanish;
length Word $100;
array W[&MaxN] $100;
do i = 1 to &MaxN;
   input Number Word 5-50;
   W[i] = Word;
end;
drop i Number Word;
datalines;
1   uno
2   dos
3   tres
4   cuatro
5   cinco
6   seis
7   siete
8   ocho
9   nueve
10  diez
11  once
12  doce
13  trece
14  catorce
15  quince
16  dieciseis
17  diecisiete
18  dieciocho
19  diecinueve
20  veinte
21  veintiuno
22  veintidos
23  veintitres
24  veinticuatro
25  veinticinco
26  veintiseis
27  veintisiete
28  veintiocho
29  veintinueve
30  treinta
;

The name of the data set is "Spanish." You can specify the data set name and an initial number (less than or equal to 30) to play the Number-Word Game in Spanish, as follows:

%NumberWordGame(Spanish, 19);  /* period 2 */

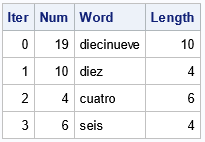
When the initial number is 19, the output shows that the generated sequence is 19 → 10 → 4 → 6. The next number would be 4 ("seis" has four letters), so the algorithm stops because it detects that the sequence will repeat {4, 6, 4, 6, ...} forever.

Let's try a different number, 20:

%NumberWordGame(Spanish, 20);  /* period 2 */

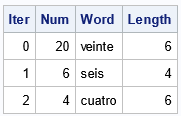
The output is similar. Again, the sequence is attracted to a period-two cycle: 20 → 6 → 4, after which the sequence {6, 4, 6, 4, ...} will repeat forever. Does every number converge to the period-two cycle? No. The Spanish word for 5 is "cinco", which has five letters, therefore 5 is a fixed point. The number 21 is an example that converges to the fixed point at 5:

%NumberWordGame(Spanish, 21);  /* fixed point */

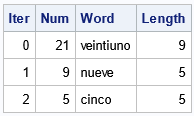
For the Spanish language, every initial value converges either to 5 or to the period-two cycle {4, 6}.

The Number-Word Game in Klingon

You can apply the algorithm to any alphabetic language, real or fictional. To demonstrate, let's consider the fictional language of Klingon, which was developed for the Star Trek movies and television series. The Klingon language was created by Marc Okrand, a professor of linguistics at the University of California. You can read about how to count in Klingon, or just run the following SAS DATA step:

/* Read the Klingon numbers 1-30 into an array */
%let MaxN = 30;
data Klingon;
length Word $100;
array W[&MaxN] $100;
do i = 1 to &MaxN;
   input Number Word 5-50;
   W[i] = Word;
end;
drop i Number Word;
datalines;
1   wa' 
2   cha' 
3   wej 
4   loS 
5   vagh 
6   jav 
7   Soch 
8   chorgh 
9   Hut 
10  wa'maH 
11  wa'maH wa' 
12  wa'maH cha' 
13  wa'maH wej 
14  wa'maH loS 
15  wa'maH vagh 
16  wa'maH jav 
17  wa'maH Soch 
18  wa'maH chorgh 
19  wa'maH Hut 
20  cha'maH 
21  cha'maH wa' 
22  cha'maH cha' 
23  cha'maH wej 
24  cha'maH loS 
25  cha'maH vagh 
26  cha'maH jav 
27  cha'maH Soch 
28  cha'maH chorgh 
29  cha'maH Hut 
30  wejmaH 
;
 
/* all iterations converge to 3 ("wej") */
%NumberWordGame(Klingon, 20);
%NumberWordGame(Klingon, 25);

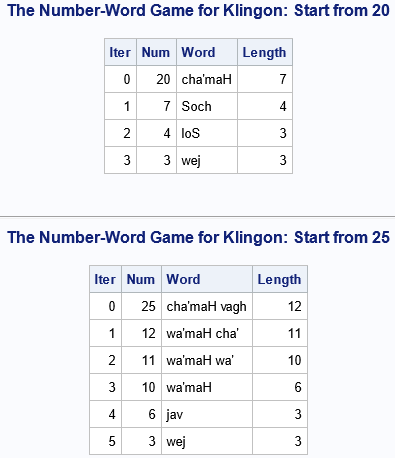
The output shows the Klingon version of the Number-Word Game for two input values. Both converge to 3 ("wej") after a few iterations. You can play the game for the values 1–30 to convince yourself that all input values converge to 3 for the Klingon language. This result is very appropriate if you are familiar with the Klingon culture: there is fixed point that is dominant; all other numbers follow a path that leads to the dominant fixed point!

Limitations of the implementation

The main limitation in this implementation is that you must create a data set that associates numbers and words for each language. When I demonstrated the English version of the Number-Word Game, I used the WORDSw. format in SAS to automatically generated the words from the numbers. Alas, SAS does not provide a format that converts numbers to Klingon, so you must manually input the word for each number.

By running the program for a variety of input values, you can claim that the algorithm converges to a fixed point of a limit cycle. The correctness of this claim assumes that the language has the following property: There exists a natural number, G, such that for all natural numbers n > G, the character representation of n has fewer than n characters. This forces the sequence to be strictly decreasing for n > G. You can then manually check the behavior of the sequence for the finite values 1–G to discover the fixed points and periodic cycles. In English, G = 5. In Spanish, G = 5. In Klingon, G = 3.

Your turn to play the game

It's your turn! Want to play the Number-Word Game in your favorite language? Do the following:

1. Create a SAS data set that contains the variables W1–W30 that contains the character representation of the numbers 1–30. Use the Spanish data set as an example.
2. Run the %NumberWordGame macro for one input value to make sure it works. For example, run
   %NumberWordGame(Spanish, 20);
   Does the sequence terminate with a fixed point or a periodic cycle?
3. Run the %NumberWordGame macro for all inputs 1–30 to determine all possible behaviors. To help, you can run the following macro, which plays the game a specified number of times for a sequence of inputs:

   %macro PlayGames(Language, maxN); %do i = 1 %to &maxN; %NumberWordGame(&Language, &i); %end; %mend;   %PlayGames(Spanish, 10); /* Play the Spanish game for inputs 1-10 */

4. Post a comment and let me know the fixed points and/or periodic cycles for your language. Does any language have a periodic cycle of length 3 or 4? Use the following template to report your results. Replace the boldface words to match your language. Note: Your language might have more than one fixed point and/or more than one periodic cycle! Or it might have only a fixed point or only a periodic cycle.
   I ran the Number-Word Game for Spanish.
   A fixed point is 5 ("cinco").
   A periodic cycle is 4 ("cuatro") and 6 ("seis").