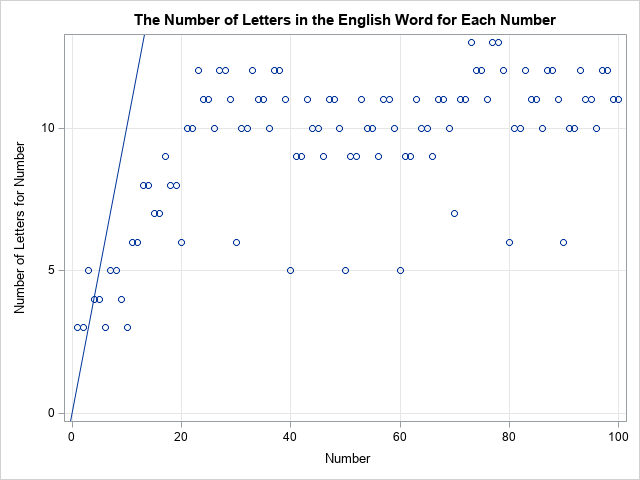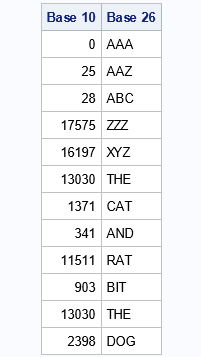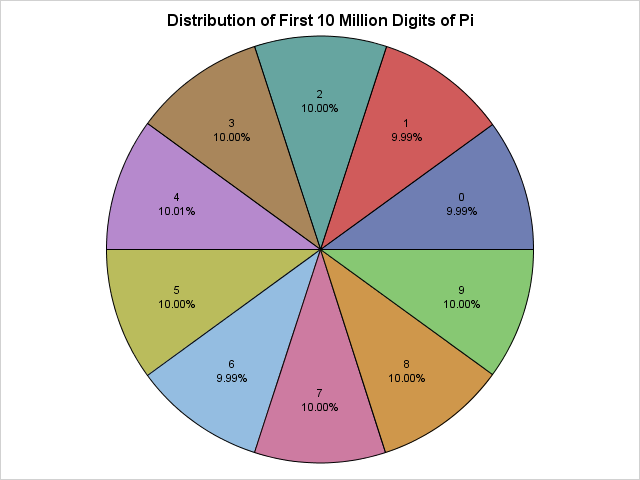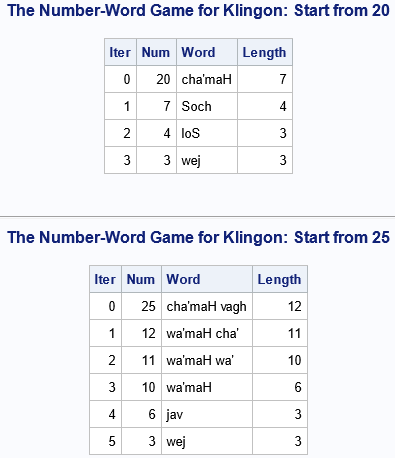
I recently wrote about the Number-Word Game, which is an iterative algorithm that generates a sequence of natural numbers by using the lengths of the words for the numbers. In English, the words are "one", "two", "three", and so on. You can play the Number-Word Game in any alphabetic language
Have you heard about the Number-Word Game? This is a simple game that has the following rules: Start with any positive integer. Write down the English word for the integer. Count the number of letters in the word. This gives a new positive integer. Go to (2). Repeat until a
Some hearts are famous. For example, there is the "Heart of Gold" (Neil Young), the "Heart of Glass" (Blondie), and the Heart of Darkness (Joseph Conrad). But have you heard of the "Heart of Ellipses"? No? Well, in 2023, Ted Conway published an amusingly titled article, "Total Ellipse of the
SAS programmers love to make special graphs for Valentine's Day. In fact, there is a long history of heart-shaped graphs and love-inspired programs written in SAS! Last year, I added to the collection by showing how a ball bounces on a heart-shaped billiards table. This year, I create a similar
For Christmas 2021, I wrote an article about palettes of Christmas colors, chiefly shades of red, green, silver, and gold. One of my readers joked that she would like to use my custom palette to design her own Christmas wrapping paper! I remembered her jest when I saw some artwork
One of the benefits of social media is the opportunity to learn new things. Recently, I saw a post on Twitter that intrigued me. The tweet said that the expected volume of a random tetrahedron in the unit cube (in 3-D) is E[Volume] = 0.0138427757.... This number seems surprisingly small!
I recently showed how to represent positive integers in any base and gave examples of base 2 (binary), base 8 (octal), and base 16 (hexadecimal). One fun application is that you can use base 26 to associate a positive integer to every string of English characters. This article shows how
On this Pi Day, let's explore the "πth roots of unity." (Pi Day is celebrated in the US on 3/14 to celebrate π ≈ 3.14159....) It's okay if you've never heard of the πth roots of unity. This article starts by reviewing the better-known nth roots of unity. It then
Did you know that you can use π to partition the positive integers into two disjoint groups? It's not hard. One group is generated by the integer portions of multiples of π. The FLOOR function gives the integer portion of a positive number, so you can write integer that are
For some reason, SAS programmers like to express their love by writing SAS programs. Since Valentine's Day is next week, I thought I would add another SAS graphic to the collection of ways to use SAS to express your love. Last week, I showed how to use vector operation and
I recently showed how to find the intersection between a line and a circle. While working on the problem, I was reminded of a fun mathematical game. Suppose you make a billiard table in the shape of a circle or an ellipse. What is the path for a ball at
Suppose you are creating a craft project for the Christmas holidays, and you want to choose a palette of Christmas colors to give it a cheery holiday appearance. You could use one of the many online collections of color palettes to choose a Christmas-themed palette. However, I didn't want to
In a previous article, I discussed a beautiful painting called "Phantom’s Shadow, 2018" by the Nigerian-born artist, Odili Donald Odita. I noted that if you overlay a 4 x 4 grid on the painting, then each cell contains a four-bladed pinwheel shape. The cells display rotations and reflections of the pinwheel. The
Art evokes an emotional response in the viewer, but sometimes art also evokes a cerebral response. When I see patterns and symmetries in art, I think about a related mathematical object or process. Recently, a Twitter user tweeted about a painting called "Phantom’s Shadow, 2018" by the Nigerian-born artist, Odili
Most games of skill are transitive. If Player A wins against Player B and Player B wins against Player C, then you expect Player A to win against Player C, should they play. Because of this, you can rank the players: A > B > C Interestingly, not all games
In the paper "Tips and Techniques for Using the Random-Number Generators in SAS" (Sarle and Wicklin, 2018), I discussed an example that uses the new STREAMREWIND subroutine in Base SAS 9.4M5. As its name implies, the STREAMREWIND subroutine rewinds a random number stream, essentially resetting the stream to the beginning.
What is this math good for, anyway? –Every student, everywhere I am a professional applied mathematician, yet many of the mathematical and statistical techniques that I use every day are not from advanced university courses but are based on simple ideas taught in high school or even in grade school.
It's time to celebrate Pi Day! Every year on March 14th (written 3/14 in the US), math-loving folks celebrate "all things pi-related" because 3.14 is the three-decimal approximation to the mathematical constant, π. Although children learn that pi is approximately 3.14159..., the actual definition of π is the ratio of
The best way to spread Christmas cheer is singing loud for all to hear! -Buddy in Elf In the Christmas movie Elf (2003), Jovie (played by Zooey Deschanel) must "spread Christmas cheer" to help Santa. She chooses to sing "Santa Claus is coming to town," and soon all of New
Last week I compared the overhand shuffle to the riffle shuffle. I used random operations to simulate both kinds of shuffles and then compared how well they mix cards. The article caused one my colleague and fellow blogger, Rob Pratt, to ask if I was familiar with a bit of
My colleague Robert Allison recently blogged about using the diameter of Texas as a unit of measurement. The largest distance across Texas is about 801 miles, so Robert wanted to find the set of all points such that the distance from the point to Texas is less than or equal
Out of the bosom of the Air, Out of the cloud-folds of her garments shaken, Over the woodlands brown and bare, Over the harvest-fields forsaken, Silent, and soft, and slow Descends the snow. "Snow-flakes" by Henry Wadsworth Longfellow Happy holidays to all my readers! In my last post I showed
I have a fondness for fractals. In previous articles, I've used SAS to create some of my favorite fractals, including a fractal Christmas tree and the "devil's staircase" (Cantor ) function. Because winter is almost here, I think it is time to construct the Koch snowflake fractal in SAS. A
Last week I blogged about how to draw the Cantor function in SAS. The Cantor function is used in mathematics as a pathological example of a function that is constant almost everywhere yet somehow manages to "climb upwards," thus earning the nickname "the devil's staircase." The Cantor function has three
I was a freshman in college the first time I saw the Cantor middle-thirds set and the related Cantor "Devil's staircase" function. (Shown at left.) These constructions expanded my mind and led me to study fractals, real analysis, topology, and other mathematical areas. The Cantor function and the Cantor middle-thirds
Lo how a rose e'er blooming From tender stem hath sprung As I write this blog post, a radio station is playing Chrismas music. One of my favorite Christmas songs is the old German hymn that many of us know as "Lo, How a Rose E're Blooming." I was humming
In my previous blog post, I showed how you can use SAS to program a "weaving" algorithm that takes an image, cuts it into strips, and weaves the strips together to create mathematical art. I used matrices and heat maps for the computations and visualization. At the end of the
An artist friend of mine recently created a beautiful abstract image and described the process on her blog. She says that "after painting my initial square, I cut it into strips and split them down the middle, then wove them together.... I had no idea when I started piecing these
Last week I was chatting with some mathematicians and I mentioned the blog post that I wrote last year on the distribution of Pythagorean triples. In my previous article, I showed that there is an algorithm that uses matrix multiplication to generate every primitive Pythagorean triple by starting with the
Saturday, March 14, 2015, is Pi Day, and this year is a super-special Pi Day! This is your once-in-a-lifetime chance to celebrate the first 10 digits of pi (π) by doing something special on 3/14/15 at 9:26:53. Apologies to my European friends, but Pi Day requires that you represent dates
