It's time to celebrate Pi Day! Every year on March 14th (written 3/14 in the US), math-loving folks celebrate "all things pi-related" because 3.14 is the three-decimal approximation to the mathematical constant, π. Although children learn that pi is approximately 3.14159..., the actual definition of π is the ratio of a circle's circumference to its diameter. Equivalently, it is distance around half of the unit circle. (The unit circle has a unit radius, so its diameter is 2.) The value for pi, therefore, depends on the definition of a circle.

But we all know what a circle looks like, don't we? How can there be more than one circle?

Generalizing the circle

A circle is defined as the locus of points in the plane that are a given distance from a given point. This definition depends on the definition of a "distance," and it turns out that there are infinitely many ways to measure the distance between two points in the plane. The Euclidean distance between two points is the most familiar distances, but there are other definitions. For two points a = (x1, y1) and b = (x2, y2), you can define the "L^p distance" between a and b by the formula
D_p = ( |x1 – x2|^p + |y1 – y2|^p )^1/p
This definition defines a distance metric for every value of p ≥ 1. If you set p=2 in the formula, you get the usual L² (Euclidean) distance. If you set p=1, you get the L¹ metric, which is known as the "taxicab" or "city block" distance.

You might think that the Euclidean distance is the only relevant distance, but it turns out that some of these other distances have practical applications in statistics, machine learning, linear algebra, and many fields of applied mathematics. For example, the 2-norm (L²) distance is used in least-squares regression whereas the 1-norm (L¹) distance is used in robust regression and quantile regression. A combination of the two distances is used for ridge regression, LASSO regression, and "elastic net" regression.

Here's the connection to pi: If you can define infinitely many distance formulas, then there are infinitely many unit circles, one for each value of p ≥ 1. And if there are infinitely many circles, there might be infinitely many values of pi. (Spoiler alert: There are!)

Would the real circle please stand up?

You can easily solve for y as a function of x and draw the unit circle for a representative set of values for p. The following graph was generated by the SAS step and PROC SGPLOT. You can download the SAS program that generates the graphs in this article.

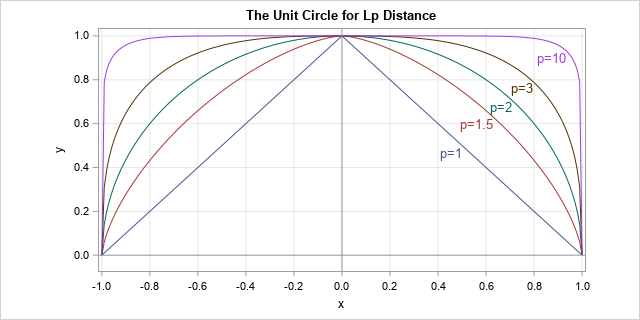
The L¹ unit circle is a diamond (the top half is shown), the L² unit circle is the familiar round shape, and as p gets large the unit circle for the L^p distance approaches the boundary of the square defined by the four points (±1, ±1). For more information about L^p circles and metrics, see the Wikipedia article "Lp Space: The p-norm in finite dimensions."

Here comes the surprise: Just as each L^p metric has its own unit circle, each metric has its own numerical value for pi, which is the length of the unit semicircle as measured by that metric.

π(p): The length of the unit semicircle for the L^p distance metric

So far, we've only used geometry, but it's time to use a little calculus. This presentation is based on Keller and Vakil (2009, p. 931-935), who give more details about the formulas in this section.

For a curve that is represented as a graph (y as a function of x), you can obtain the length of the curve by integrating the arclength. In Calculus 2, the arclength formula is derived for Euclidean distance, but it is straightforward to give the formula for the L^p distance:
s(p) = ∫ (1 + |dy/dx|^p)^1/p dx

To obtain a value for pi in the L^p metric, you can integrate the arclength for the upper half of the L^p unit circle. Equivalently, by symmetry, you can integrate one-eighth of the unit circle and multiply by 4. A convenient choice for the limits of integration is [0, 2^-1/p] because 2^-1/p is the x value where the 45-degree line intersects the unit circle for the L^p metric.

Substituting for the derivative gives the following formula (Keller and Vakil, 2009, p. 932):
π(p) = 4 ∫ (1 + u(x))^1/p dx, where u(x) = |x^-p - 1|^1-p and the interval of integration is [0, 2^-1/p].

A pi for each L^p metric

For each value of p, you get a different value for pi. You can use your favorite numerical integration routine to approximate π(p) by integrating the formula for various values of p ≥ 1. I used SAS/IML, which supports the QUAD function for numerical integration. The arclength computation for a variety of values for p is summarized by the following graph. The graph shows the computation of π(p), which is the length of the semicircle in the L^p metric, versus values of p for p in [1, 11].

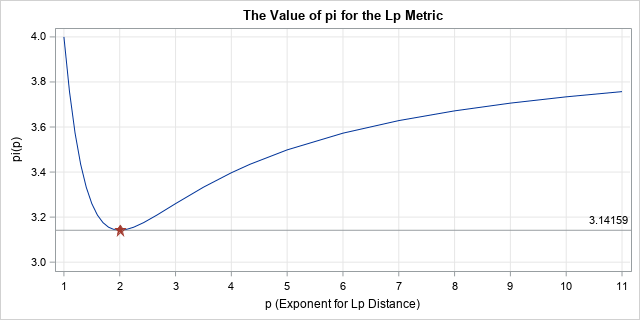
The graph shows that the L¹ value for pi is 4. The value decreases rapidly as p approaches 2 and reaches a minimum value when p=2 and the value of pi is 3.14159.... For p > 2, the graph of π(p) increases slowly. You can show that π(p) asymptotically approaches the value 4 as p approaches infinity.

On Pi Day, some places have contests to see who can recite the most digits of pi. I encourage you to enter the contest and say "Pi, in the L¹ metric, is FOUR point zero, zero, zero, zero, ...." If they refuse to give you the prize, tell them to read this article! 😉

Reflections on pi

One the one hand, this article shows that there is nothing special about the value 3.14159.... For an L^p metric, the ratio of the circumference of a circle to its diameter can be any value between π and 4. On the other hand, the graph shows that π is the unique minimizer of the graph. Among an infinitude of circles and metrics, the well-known Euclidean distance is the only L^p metric for which pi is 3.14159....

If you ask me, our value of π is special, without a doubt!

References

Download the SAS program that creates the graphs in this article.

• C. L. Adler and J. Tanton (2000) "π is the Minimum Value for Pi", The College Mathematics Journal, 31:2, 102-106.
• J. B. Keller and R. Vakil (2009) "π_p, the Value of π in l_p", The American Mathematical Monthly, 116:10, 931-935.