The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs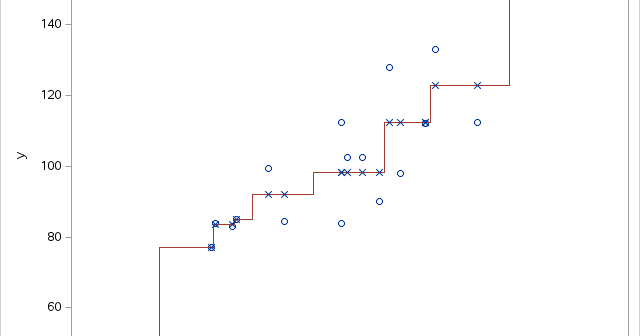
Since the pandemic began in 2020, the SAS IML developers have added about 50 new functions and enhancements to the SAS IML language in SAS Viya. Among these functions are new modern methods for optimization that have a simplified syntax as compared to the older 'NLP' functions that are available
Just like the SAS DATA step, the SAS IML language supports both functions and subroutines. A function returns a value, so the calling syntax is familiar: y = func(x1, x2); /* the function returns one value, y */ In this syntax, the input arguments are x1 and x2. The

Isotonic regression (also called monotonic regression) is a type of regression model that assumes that the response variable is a monotonic function of the explanatory variable(s). The model can be nondecreasing or nonincreasing. Certain physical and biological processes can be analyzed by using an isotonic regression model. For example, a

A previous article discusses the fact that there are often multiple ways in SAS to obtain the same result. This fact results in many vigorous discussions on online programming forums as people propose different (but equivalent) methods for solving someone's problem then argue why their preferred method is better than

As announced and demonstrated at SAS Innovate 2024, SAS plans to include a generative AI assistant called SAS Viya Copilot in the forthcoming SAS Viya Workbench. You can submit a text prompt (by putting it in a comment string) and the Copilot will generate SAS code for you. My colleagues
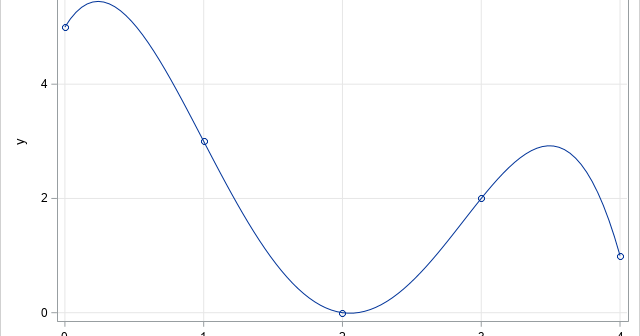
While reviewing a book on numerical analysis, I was reminded of a classic interpolation problem. Suppose you have n pairs of points in the plane: (x1,y1), (x2,y2), ..., (xn,yn), where the first coordinates are distinct. Then you can construct a unique polynomial of degree (at most) n-1 that passes through
