The Number-Word Game

Have you heard about the Number-Word Game? This is a simple game that has the following rules:

Start with any positive integer.
Write down the English word for the integer.
Count the number of letters in the word. This gives a new positive integer.
Go to (2). Repeat until a portion of the sequence repeats itself.

Here is an example of playing the Number-Word Game:

Start with 7.
The English word for 7 is seven, which has five letters. Therefore, the next integer is 5.
The English word for 5 is five, which has four letters. Therefore, the next integer is 4.
The English word for 4 is four, which has four letters. Therefore, the next integer is 4. The sequence is repeating itself ( 4, 4, 4, ...), so the game stops.

Here's an interesting fact: For the English version of the Number-Word Game, the sequence ALWAYS reaches 4! In the terminology of discrete dynamical systems, the number 4 is a globally attracting fixed point for the iterative algorithm. No matter what initial natural number you choose, the game always ends with 4.

This game makes a fun programming exercise in SAS because SAS contains a special format (the WORDSw. format) that can automatically convert integers to the equivalent English word. This article shows how to use the WORDS. format to play the Number-Word Game.

The WORDS. format in SAS

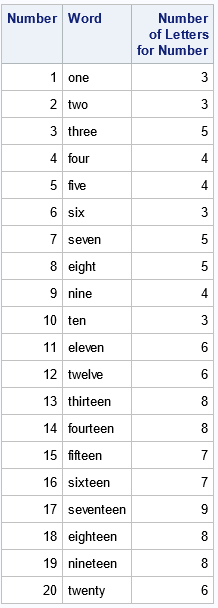
The WORDS. format in SAS converts numbers to words. By using the format, you do not have to type the English words for the natural numbers! Instead, you can use the PUTN function to convert an integer into the equivalent English word. You can then use the LENGTH function to find the length of the word. To demonstrate these functions, the following SAS DATA step generates the natural numbers 1–20, the corresponding English word, and the length of the English word:

data NumberWords;
length Word $200;
do Number = 1 to 20;
   Word = putn(Number, "WORDS200.");
   Length = length(Word);
   output;
end;
label Length="Number of Letters for Number";
run;
 
proc print data=NumberWords label noobs; 
   var Number Word Length;
run;

The output is shown at the top of this article. You can use the table to play the Number-Word Game for any integer up to 20. For example, suppose you choose 20 as an initial number. According to the table, the word twenty has 6 letters, so go to row 6. The word six has 3 letters, so go to row 3. The remaining sequence is 3 → 5 → 4, which ends the game.

You can use the table to convince yourself that every starting number in the table eventually reaches 4, and the game ends.

Automate playing the Number-Word Game

You can program the Number-Word Game if you know the number of letters in the word that represents each natural number. The following SAS macro uses a DATA step to compute the iteration history of the game when you specify an initial number.

/* English version of the Number-Word Game.
   You specify an initial natural number. The program shows the 
   iteration of the Number-Word Game, which always reaches the number 4.
*/
%macro NumberWordIteration(N0);
data IterHistory;
Iter = 0; N = &N0; Word = putn(N, "WORDS200."); Length=length(Word);
output;
do Iter=1 to 100 while (N ^= Length);  /* stop if reach fixed point */
   N = length( Word );
   Word = putn(N, "WORDS200.");
   Length=length(Word);
   output;
end;
run;
 
proc print data=IterHistory noobs;
run;
%MEND;

With the help of the program, we can play the game for very large numbers. For example, the following statement plays the game for 673:

%EnglishWordIteration(673);

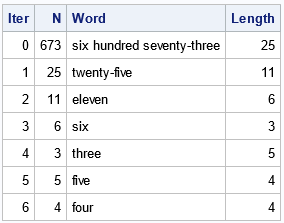
Are you surprised that the game terminates after only six steps? That length is fairly typical! The word for 673 has only 25 letters, so the next number is much smaller than the first number. The word twenty-five has only 11 letters, and we've previously noted that every natural number less than 20 terminates at 4.

Let's try it again with an even larger initial number:

%EnglishWordIteration(12345);

For the number 12,345, the game terminates in only three iterations! The sequence is 40 → 5 → 4.

Sketch of a proof

You can prove that the English version of the Number-Word Game terminates at the number 4 for every starting number. First, prove that the number of letters for the number N is less than N for all N ≥ 5. This implies that the sequence in the game is a strictly decreasing sequence until the sequence becomes 4 or less. In the second step, manually check the result of the game for 1, 2, 3, and 4. That completes the proof.

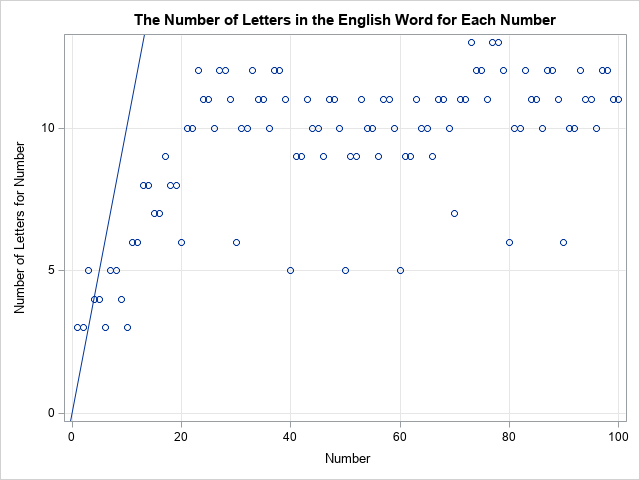
The following graph shows the number of letters in the English word for each natural number 1–100. The diagonal line is the identity line y=x. All markers for numbers greater than 4 are underneath the identity line. This shows that if N is greater than 4, the number of letters in the word for N is less than N.

The limits of the implementation

On my Windows PC, it appears that the WORDSw. format can produce the words for numbers up to 999,999,999. Numbers that are one billion or larger are formatted as "large_number."

For numbers less than one billion, I think the number that has the longest character representation is 777,777,777, which requires 100 characters (including spaces) to represent. The iteration history for that number requires only six iterations before reaching the fixed point: 100 → 11 → 6 → 3 → 5 → 4.

Summary

The Number-Word Game is an algorithm that can be easily programmed in SAS by using the WORDSw. format and the LENGTH function. This article shows how to write a simple SAS program that plays the Numbers-Word Game. For English words, the Number-Word Game always terminates after a small number of steps. The number 4 is a global attracting fixed point for the algorithm.

Blogs