They say nothing in life is certain other than death and taxes, but there something else I’ve found I can count on from experience: sending out invites for a party on social media only to receive a few affirmative responses and a whole slew of “maybe”. I know my friends
A remarkable result in probability theory is the "three-sigma rule," which is a generic name for theorems that bound the probability that a univariate random variable will appear near the center of its distribution. This article discusses the familiar three-sigma rule for the normal distribution, a less-familiar rule for unimodal
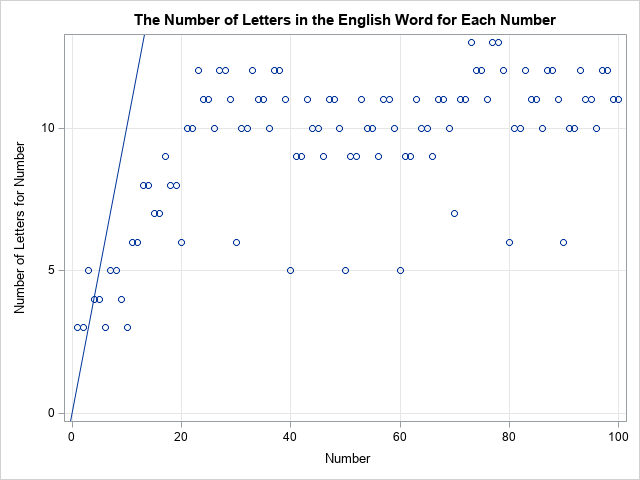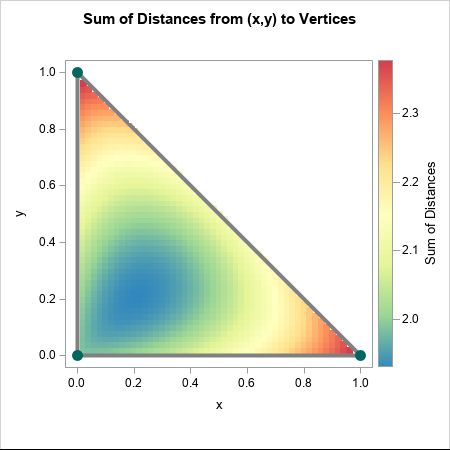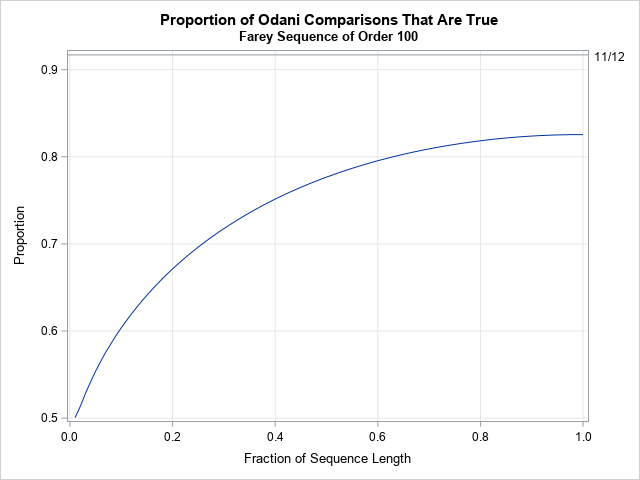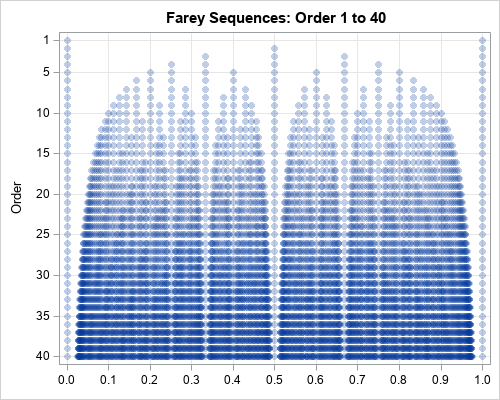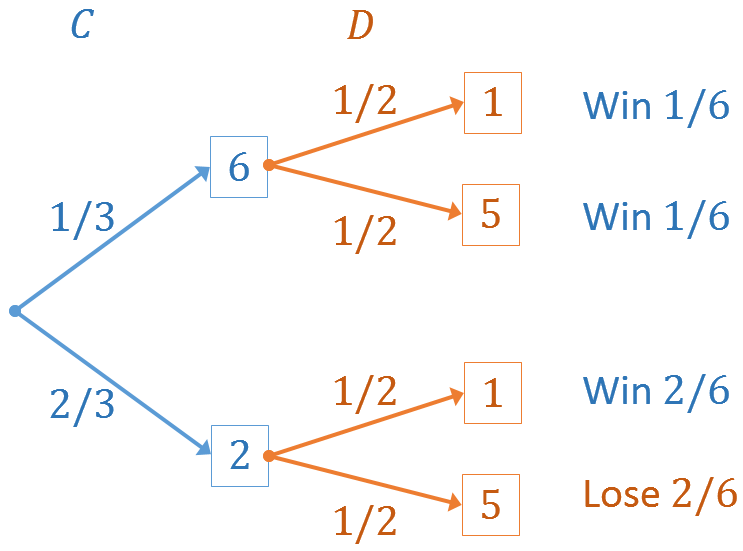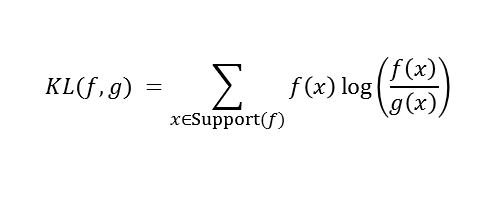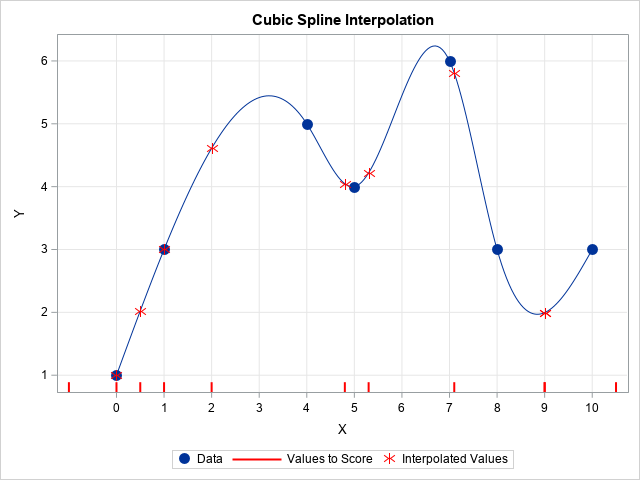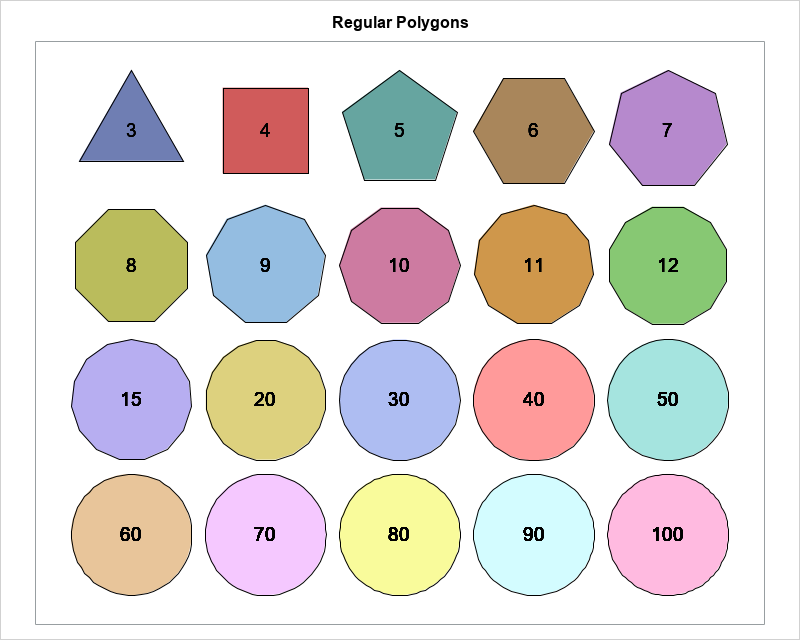
Happy Pi Day! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate all things pi-related because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979.... Pi is a mathematical constant defined as the ratio of a circle's circumference (C) to its diameter (D).
Have you heard about the Number-Word Game? This is a simple game that has the following rules: Start with any positive integer. Write down the English word for the integer. Count the number of letters in the word. This gives a new positive integer. Go to (2). Repeat until a
Some hearts are famous. For example, there is the "Heart of Gold" (Neil Young), the "Heart of Glass" (Blondie), and the Heart of Darkness (Joseph Conrad). But have you heard of the "Heart of Ellipses"? No? Well, in 2023, Ted Conway published an amusingly titled article, "Total Ellipse of the
October 13 is National M&M Day in the US. It’s a time to reignite the debate about whether you can taste the difference between the different colored chocolate-filled candies. If you’re like me, equally as enjoyable as eating M&Ms is taking a crack at how many of them are in
While writing an article about labeling a polygon by using the centroid, I almost made a false claim about the centroid. I almost claimed that that the centroid is the point in a polygon that minimizes the sum of the distances to the vertices. It is not. The point that
The area of a convex hull enables you to estimate the area of a compact region from a set of discrete observations. For example, a biologist might have multiple sightings of a wolf pack and want to use the convex hull to estimate the area of the wolves' territory. A
On this Pi Day, let's explore the "πth roots of unity." (Pi Day is celebrated in the US on 3/14 to celebrate π ≈ 3.14159....) It's okay if you've never heard of the πth roots of unity. This article starts by reviewing the better-known nth roots of unity. It then
Did you know that you can use π to partition the positive integers into two disjoint groups? It's not hard. One group is generated by the integer portions of multiples of π. The FLOOR function gives the integer portion of a positive number, so you can write integer that are
For some reason, SAS programmers like to express their love by writing SAS programs. Since Valentine's Day is next week, I thought I would add another SAS graphic to the collection of ways to use SAS to express your love. Last week, I showed how to use vector operation and
I recently showed how to find the intersection between a line and a circle. While working on the problem, I was reminded of a fun mathematical game. Suppose you make a billiard table in the shape of a circle or an ellipse. What is the path for a ball at
Suppose you are creating a craft project for the Christmas holidays, and you want to choose a palette of Christmas colors to give it a cheery holiday appearance. You could use one of the many online collections of color palettes to choose a Christmas-themed palette. However, I didn't want to
The number of possible bootstrap samples for a sample of size N is big. Really big. Recall that the bootstrap method is a powerful way to analyze the variation in a statistic. To implement the standard bootstrap method, you generate B random bootstrap samples. A bootstrap sample is a sample
Art evokes an emotional response in the viewer, but sometimes art also evokes a cerebral response. When I see patterns and symmetries in art, I think about a related mathematical object or process. Recently, a Twitter user tweeted about a painting called "Phantom’s Shadow, 2018" by the Nigerian-born artist, Odili
Odani's truism is a mathematical result that says that if you want to compare the fractions a/b and c/d, it often is sufficient to compare the sums (a+d) and (b+c) rather than the products a*d and b*c. (All of the integers a, b, c, and d are positive.) If you
Quick! Which fraction is bigger, 40/83 or 27/56? It's not always easy to mentally compare two fractions to determine which is larger. For this example, you can easily see that both fractions are a little less than 1/2, but to compare the numbers you need to compare the products 40*56
Here is an interesting math question: How many reduced fractions in the interval (0, 1) have a denominator less than 100? The question is difficult is because of the word "reduced." If we only care about the total number of fractions in (0,1) whose denominator is less than 100, we
Do you know that you can create a vector that has a specific correlation with another vector? That is, given a vector, x, and a correlation coefficient, ρ, you can find a vector, y, such that corr(x, y) = ρ. The vectors x and y can have an arbitrary number
Most games of skill are transitive. If Player A wins against Player B and Player B wins against Player C, then you expect Player A to win against Player C, should they play. Because of this, you can rank the players: A > B > C Interestingly, not all games
SAS has always believed in the power of education, but in today’s data-driven economy, it’s more important than ever to ensure our students are introduced to data science at an early age. We as a company are focusing our resources on creating student experiences in data literacy, computer science and
If you have been learning about machine learning or mathematical statistics, you might have heard about the Kullback–Leibler divergence. The Kullback–Leibler divergence is a measure of dissimilarity between two probability distributions. It measures how much one distribution differs from a reference distribution. This article explains the Kullback–Leibler divergence and shows
I recently showed how to use linear interpolation in SAS. Linear interpolation is a common way to interpolate between a set of planar points, but the interpolating function (the interpolant) is not smooth. If you want a smoother interpolant, you can use cubic spline interpolation. This article describes how to
I've previously written about how to generate points that are uniformly distributed in the unit disk. A seemingly unrelated topic is the distribution of eigenvalues (in the complex plane) of various kinds of random matrices. However, I recently learned that these topics are somewhat related! A mathematical result called the
Recently, I saw a graphic on Twitter by @neilrkaye that showed the rapid convergence of a regular polygon to a circle as you increase the number of sides for the polygon. The author remarked that polygons that have 40 or more sides "all look like circles to me." That is,
This article discusses how to restrict a multivariate function to a linear subspace. This is a useful technique in many situations, including visualizing an objective function that is constrained by linear equalities. For example, the graph to the right is from a previous article about how to evaluate quadratic polynomials.
There are several different kinds of means. They all try to find an average value from among a set of numbers. Although the most popular mean is the arithmetic mean, the geometric mean can be useful for problems in statistics, finance, and biology. A common application of the geometric mean
What is this math good for, anyway? –Every student, everywhere I am a professional applied mathematician, yet many of the mathematical and statistical techniques that I use every day are not from advanced university courses but are based on simple ideas taught in high school or even in grade school.
The eigenvalues of a matrix are not easy to compute. It is remarkable, therefore, that with relatively simple mental arithmetic, you can obtain bounds for the eigenvalues of a matrix of any size. The bounds are provided by using a marvelous mathematical result known as Gershgorin's Disc Theorem. For certain
Last week I compared the overhand shuffle to the riffle shuffle. I used random operations to simulate both kinds of shuffles and then compared how well they mix cards. The article caused one my colleague and fellow blogger, Rob Pratt, to ask if I was familiar with a bit of
