Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
Some hearts are famous. For example, there is the "Heart of Gold" (Neil Young), the "Heart of Glass" (Blondie), and the Heart of Darkness (Joseph Conrad). But have you heard of the "Heart of Ellipses"? No? Well, in 2023, Ted Conway published an amusingly titled article, "Total Ellipse of the
This article looks at a geometric method for estimating the center of a multivariate point cloud. The method is known as convex-hull peeling. In two-dimensions, you can perform convex-hull peeling in SAS 9 by using the CVEXHULL function in SAS IML software. For higher dimensions, you can use the CONVEXHULL
A SAS programmer wanted to find the name of the variable for each row that contains the largest value. This task is useful for wide data sets in which each observation has several variables that are measured on the same scale. For example, each observation in the data might represent
A colleague remarked that my recent article about using Jacobi's iterative method for solving a linear system of equations "seems like magic." Specifically, it seems like magic that you can solve a certain class of linear systems by using only matrix multiplication. For any initial guess, the iteration converges to
In a first course in numerical analysis, students often encounter a simple iterative method for solving a linear system of equations, known as Jacobi's method (or Jacobi's iterative method). Although Jacobi's method is not used much in practice, it is introduced because it is easy to explain, easy to implement,
There are two popular ways to express the steepness of a line or ray. The most-often used mathematical definition is from high-school math where the slope is defined as "rise over run." A second way is to report the angle of inclination to the horizontal, as introduced in basic trigonometry.
Statistical software provides methods to simulate independent random variates from continuous and discrete distributions. For example, in the SAS DATA step, you can use the RAND function to simulate variates from continuous distributions (such as the normal or lognormal distributions) or from discrete distributions (such as the Bernoulli or Poisson).
In a previous article, I presented some of the most popular blog posts from 2023. The popular articles tend to discuss elementary topics that have broad appeal. However, I also wrote many technical articles about advanced topics. The following articles didn't make the Top 10 list, but they deserve a
An unobserved category is one that does not appear in a sample of data. For example, in a small sample of US voters, you are likely to observe members of the major political parties, but less likely to observe members of minor or fringe parties. This can cause a headache
In 2023, I wrote 90 articles for The DO Loop blog. My most popular articles were about SAS programming, data visualization, and statistics. In addition, several "general interest" articles were popular, including my article for Pi Day and an article about AI chatbots. If you missed any of these articles,
Statistical software often includes supports for a weight variable. Many SAS procedures make a distinction between integer frequencies and more general "importance weights." Frequencies are supported by using the FREQ statement in SAS procedures; general weights are supported by using the WEIGHT statement. An exception is PROC FREQ, which contains
SAS provides many built-in routines for data analysis. A previous article discusses polychoric correlation, which is a measure of association between two ordinal variables. In SAS, you can use PROC FREQ or PROC CORR to estimate the polychoric correlation, its standard error, and confidence intervals. Although SAS provides a built-in
Correlation is a statistic that measures the association between two variables. When two variables are positively correlated, low values of one variable tend to be associated with low values of the other variable. Medium values and high values are similarly associated. For negative correlation, the association is flipped: low values
These are a few of my favorite things. —Maria in The Sound of Music For my annual Christmas-themed post, I decided to forgo fractal Christmas trees and animated greeting cards and instead present a compilation of some of my favorite data visualization tips for advanced SAS users. Hopefully, this
A previous article discussed how to compute probabilities for the bivariate standard normal distribution. The standard bivariate normal distribution with correlation ρ is denoted BVN(0,ρ). For any point (x,y), you can use the PROBBNRM function in SAS to compute the probability that the random variables (X,Y) ~ BVN(0,ρ) is observed
This article shows how to use SAS to compute the probabilities for two correlated normal variables. Specifically, this article shows how to compute the probabilities for rectangular regions in the plane. A second article discusses the computation over infinite regions such as quadrants. If (X,Y) are random variables that are
The collinearity problem is to determine whether three points in the plane lie along a straight line. You can solve this problem by using middle-school algebra. An algebraic solution requires three steps. First, name the points: p, q, and r. Second, find the parametric equation for the line that passes
Plot rates, not counts. This maxim is often stated by data visualization experts, but often ignored by practitioners. You might also hear the related phrases "plot proportions" or "plot percentages," which mean the same thing but expresses the idea alliteratively. An example in a previous article about avoiding alphabetical ordering
Converting a program from one language to another can be a challenge. Even if the languages share many features, there is often syntax that is valid in one language that is not valid in another. Recently, a SAS programmer was converting a program from R to SAS IML. He reached
Howard Wainer, who used to write the "Visual Revelations" column in Chance magazine, often reminded his readers that "we are almost never interested in seeing Alabama first" (2005, Graphic Discovery, p. 72). His comment is a reminder that when we plot data for a large number of categories (states, countries,
Sometimes it is helpful to display a table of statistics directly on a graph. A simple example is displaying the number of observations and the mean or median on a histogram. In SAS, the term inset is used to describe a table that is displayed on a graph. This article
In several previous articles, I've shown how to use SAS to fit models to data by using maximum likelihood estimation (MLE). However, I have not previously shown how to obtain standard errors for the estimates. This article combines two previous articles to show how to obtain MLE estimates and the
A previous article shows how to use Monte Carlo simulation to approximate the sampling distribution of the sample mean and sample median. When x ~ N(0,1) are normal data, the sample mean is also normal, and there are simple formulas for the expected value and the standard error of the
An elementary course in statistics often includes a discussion of the sampling distribution of a statistic. The canonical example is the sampling distribution of the sample mean. For samples of size n that are drawn from a normally distribution (X ~ N(μ, σ)), the sample mean is normally distributed as
A previous article discusses the birthday problem and its generalizations. The classic birthday problem asks, "In a room that contains N people, what is the probability that two or more people share a birthday?" The probability is much higher than you might think. For example, in a room that contains
The birthday-matching problem (also called the birthday paradox or simply the birthday problem), is a classic problem in probability. Simply stated, the birthday-matching problem asks, "If there are N people in a room, what is the chance that two of them have the same birthday?" The problem is sometimes called
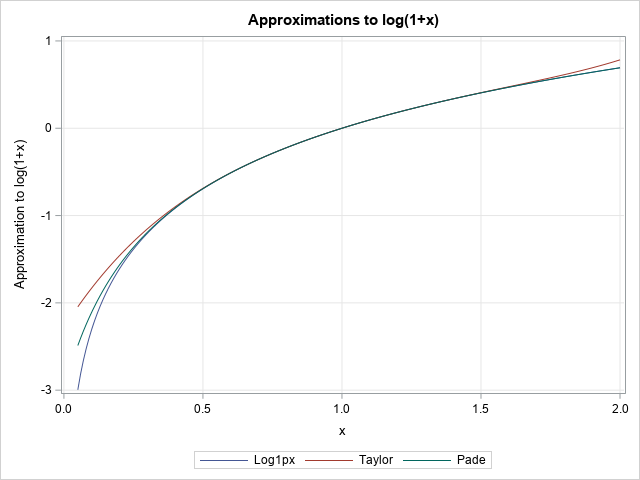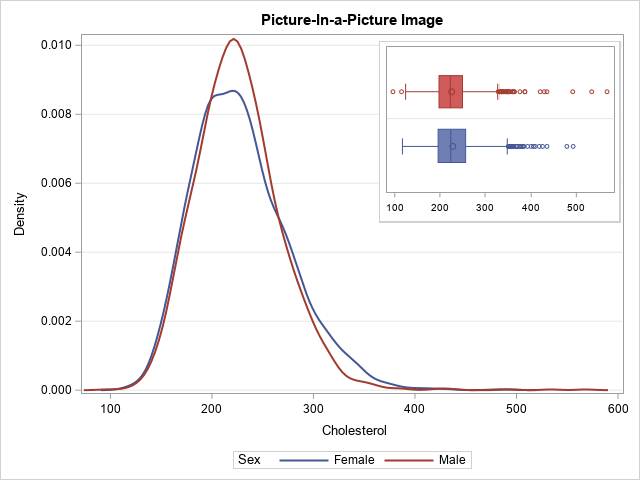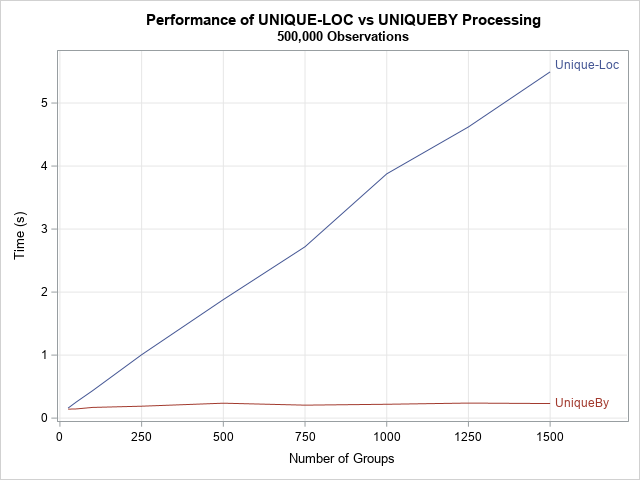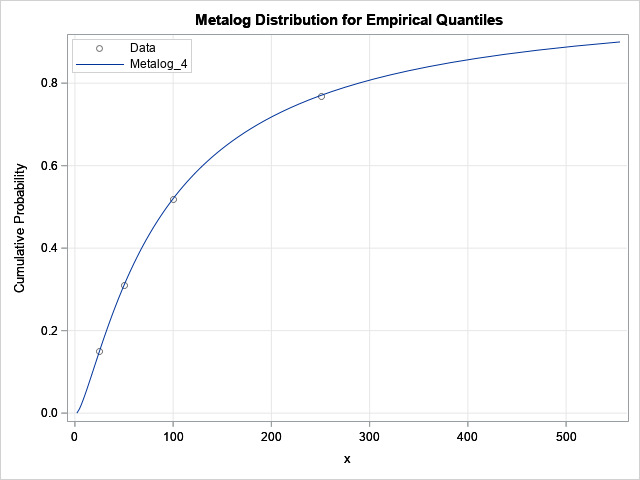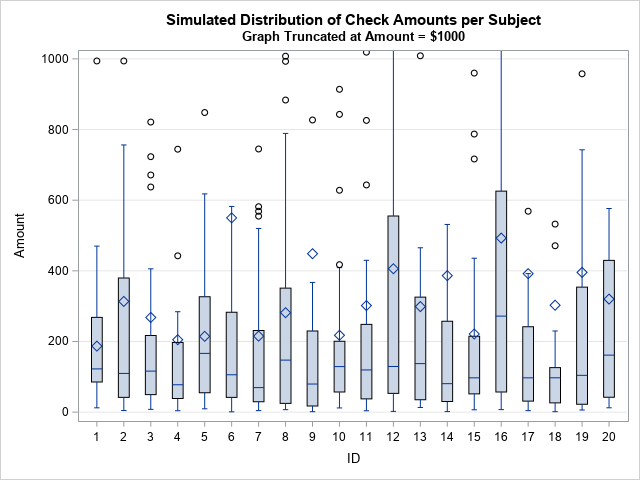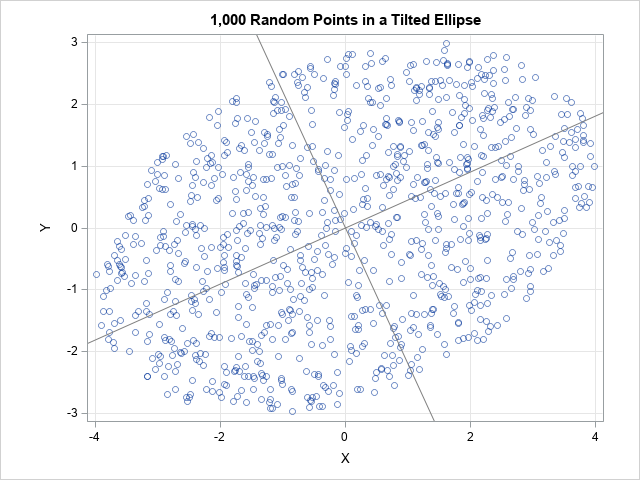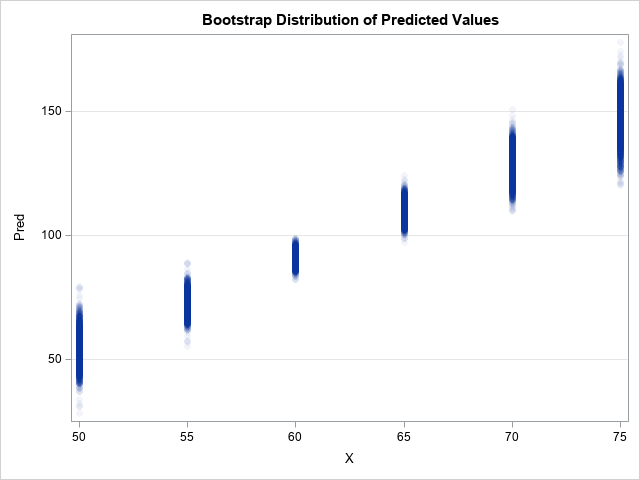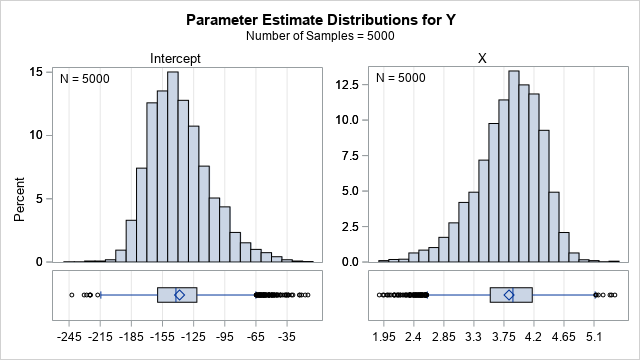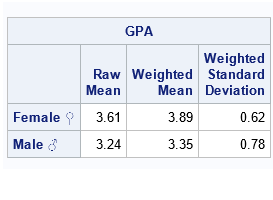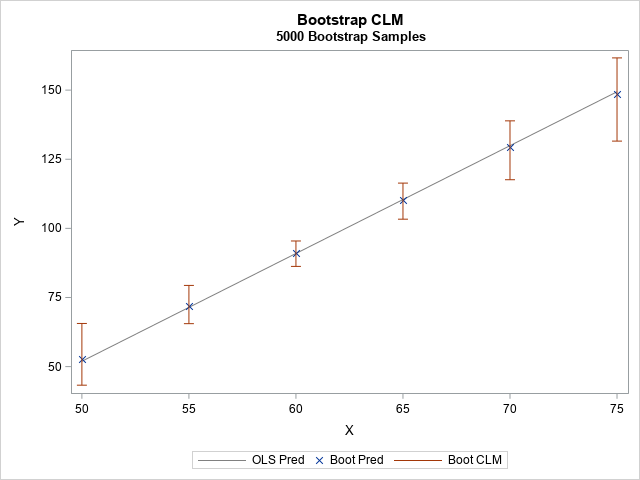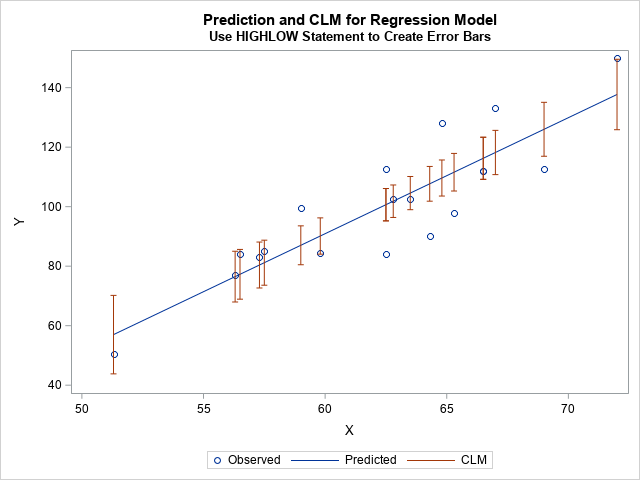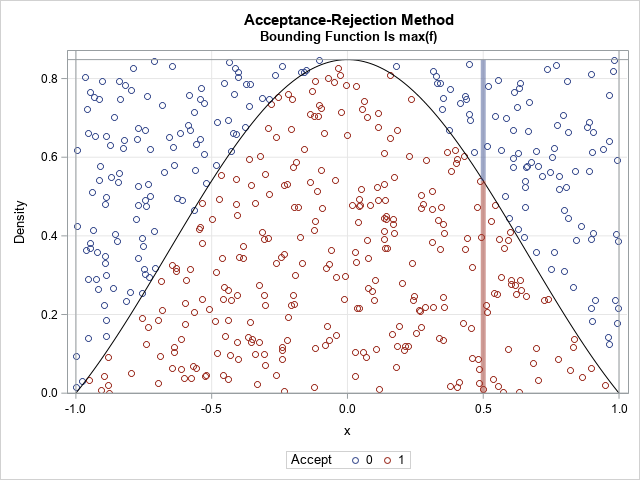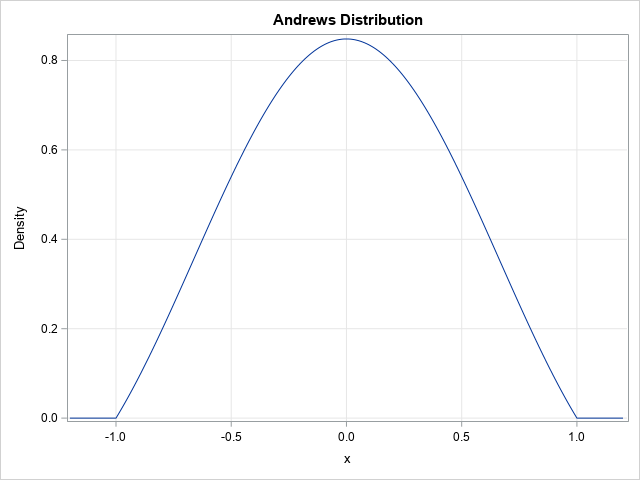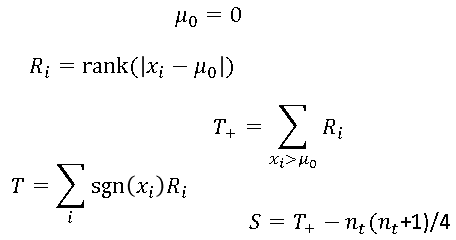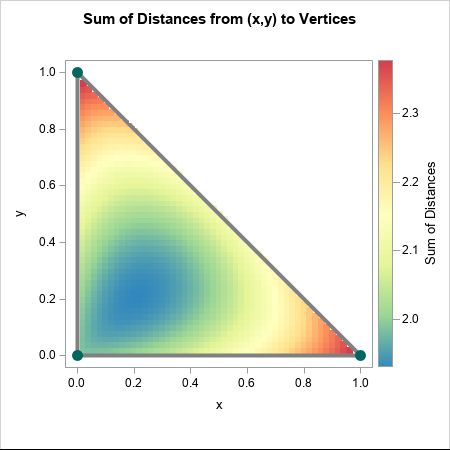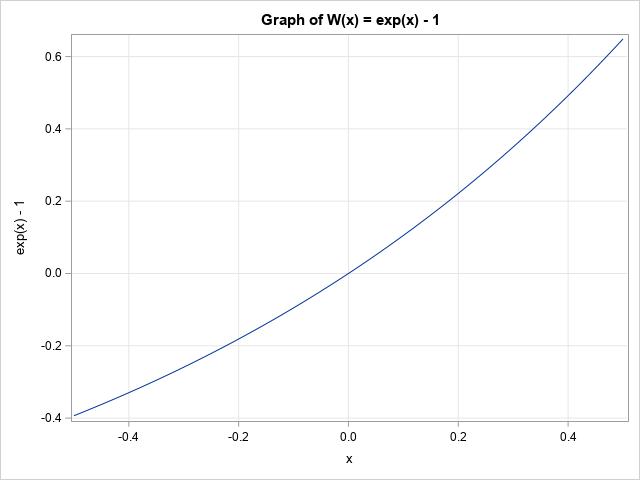
Recently I wrote about numerical analysis problem: the accurate computation of log(1+x) when x is close to 0. A naive computation of log(1+x) loses accuracy if you call the LOG function, which is why the SAS language provides the built-in LOG1PX for this computation. In addition, I showed that you
SAS supports a special function for the accurate evaluation of log(1+x) when x is near 0. The LOG1PX function is useful because a naive computation of log(1+x) loses accuracy when x is near 0. This article demonstrates two general approximation techniques that are often used in numerical analysis: the Taylor
The documentation for Python's SciPy package provides a table that concisely summarizes functions that are associated with continuous probability distributions. This article provides a similar table for SAS functions. For more information on the CDF, PDF, quantile, and random-variate functions, see "Four essential functions for statistical programmers." SAS functions for
A previous article shows ways to perform efficient BY-group processing in the SAS IML language. BY-group processing is a SAS-ism for what other languages call group processing or subgroup processing. The main idea is that the data set contains several discrete variables such as sex, race, education level, and so
