Many SAS procedures support a BY statement that enables you to perform an analysis for each unique value of a BY-group variable. The SAS IML language does not support a BY statement, but you can program a loop that iterates over all BY groups. You can emulate BY-group processing by using either of the following techniques:

1. The UNIQUE-LOC technique: You use the UNIQUE function to obtain the unique values of the BY-group variable, then use the LOC function extract all observations in the i_th BY group. The data do not need to be sorted.
2. The UNIQUEBY technique: You first sort the data, then use the UNIQUEBY function to find the first observation in each BY group. You can then directly extract all observations in the i_th BY group.

I often use the UNIQUE-LOC technique for small data sets and for a small number of BY groups. However, as I wrote way back in 2011, the UNIQUEBY technique "is more efficient than the UNIQUE-LOC technique because it does not need to use the LOC function to find the observations in each category."

For small data sets, both methods run fast, and it doesn't matter which one you use. However, I recently worked with a SAS customer to rewrite a SAS IML program that was using the UNIQUE-LOC technique. The program processes a large data set that contains a large number of groups. I was surprised by how much faster the program ran after we rewrote it to use the UNIQUEBY method. This article quantifies the performance improvement that you can gain by using the UNIQUEBY technique for BY-group processing of large data sets.

Compare the performance of UNIQUE-LOC and UNIQUEBY

Let's first compare the performance of the two methods on a moderate-sized data set that contains 20,000 observations and 500 groups. For brevity, the computation for each by group is a simple five-number summary of the observations in the group: the sample min, the max, and the sample quartiles.

The following SAS IML program generates random data. For the UNIQUE-LOC method, the program finds the levels for the 500 groups, then iterates over those levels, extracting the observations in each group. Notice that this implies that the UNIQUE-LOC method traverses the data 500 times! In contrast, the UNIQUEBY method sorts the data and finds the first row of each BY group. It can then extract each BY group without ever traversing the data.

proc iml;
N = 20000;                  /* number of observations */
numGroups = 500;            /* number of groups */
result = j(nrow(numGroups), 3, .);
result[,1] = numGroups;
 
x = randfun(N, "Normal");
ID = randfun(N, "Integer", 1, numGroups);
 
/* time the UNIQUE-LOC method */
t0 = time();
u = unique(ID);            /* get unique values of groups */
do i = 1 to ncol(u);       /* for each group */
   idx = loc(ID = u[i]);   /* find indices for the i_th BY group */
   y = x[idx];             /* extract the group */
   /* perform computations on this BY group */
   q = quartile(y);
end;
result[1,2] = time() - t0; /* time for Unique-Loc */
 
/* time the the UNIQUEBY method */
t0 = time();
z = ID || x;
call sort(z, 1);           /* sort the data by the groups */
uu = uniqueby(z[,1]);      /* get first row for each group  */
u = uu // (nrow(ID)+1);    /* trick: append (k+1) to end of indices */
do i = 1 to nrow(u)-1;     /* for each group... */
   idx = u[i]:(u[i+1]-1);  /* get rows in group */
   y = z[idx,2];           /* extract data for this BY group */
   /* perform computations on this BY group */
   q = quartile(y);
end;
result[1,3] = time() - t0; /* time for UniqueBy */
print result[c={'NumGroups' 'Time Unique-Loc' 'Time UniqueBY'} F=BEst5.];
QUIT;

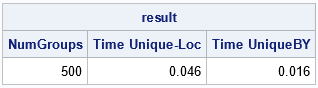
For these data, both methods are extremely fast. Yes, the UNIQUE-LOC method is three times slower, but it analyzes all 500 BY groups in 0.05 seconds. The next section increases the size of the data and also increases the number of BY groups.

Performance on larger data

The previous section noted that if a data set has n observations and k BY groups, the UNIQUE-LOC method traverses the data k times, so the performance can't be better than O(kn). For a fixed sample size, data that have many BY groups will require more time than data that have few BY groups. In contrast, the UNIQUEBY method performs one sort (O(n log(n)) and a single traversal of the data (O(n)) to find the first row for each BY group.

Consequently, if k > log(n), we expect the UNIQUEBY method to outperform the UNIQUE-LOC method. The following results are for n = 500,000 and for values of k in the range [25, 1500]. Because log₁₀(5E5) ≈ 5.7, we expect the UNIQUEBY method to outperform the UNIQUE-LOC method.

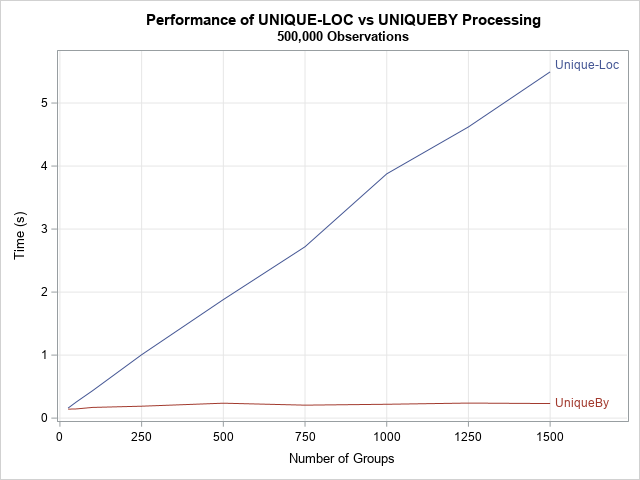
The difference in performance is noticeable. The UNIQUEBY method depends mainly on the size of the data, not on the number of BY groups. (This is not strictly correct because both algorithms perform k analyses, but I chose the analysis so that it runs very quickly.) In contrast, the UNIQUE-LOC method depends linearly on the number of BY groups. For these data and for 1,500 BY groups, the UNIQUE-LOC method requires more than 5 seconds to run, whereas the UNIQUEBY method requires only 0.2 seconds.

The Appendix displays the SAS IML program that created the plot.

Summary

When performing BY group processing in the SAS IML language, two common programming techniques are the UNIQUE-LOC method and the UNIQUEBY method. For small data sets, it doesn't matter which technique you use. However, for large data sets that have many BY groups, the UNIQUEBY method is much faster than the UNIQUE-LOC method.

Appendix

The following SAS IML program times the performance of the UNIQUE-LOC and UNIQUEBY techniques on 500,000 observations. The program simulates having k groups in the data, where k ranges between 25 and 1,500.

proc iml;
call randseed(12345);
N = 500000;                   /* number of observations */
x = randfun(N, "Normal");
 
NReps = 3;
numGroups = {25, 50, 100} // T(do(250, 1500, 250));
result = j(nrow(numGroups), 3, .);
result[,1] = numGroups;
 
do k = 1 to nrow(numGroups);  /* loop over the number of groups */
 
ID = randfun(N, "Integer", 1, numGroups[k]);
 
/* UNIQUE-LOC method */
t0 = time();
do rep = 1 to NReps;
   u = unique(ID);
   do i = 1 to ncol(u);
      idx = loc(ID = u[i]);   /* indices for the i_th BY group */
      y = x[idx];
      /* perform computations on this BY group */
      q = quartile(y);
   end;
end;
result[k,2] = (time() - t0)/NReps; /* time for Unique-Loc */
 
/* the UNIQUEBY method */
t0 = time();
do rep = 1 to NReps;
   z = ID || x;
   call sort(z, 1);
   uu = uniqueby(z[,1]);      /* get first row for each group  */
   u = uu // (nrow(ID)+1);    /* trick: append (numGroups+1) to end of indices */
   do i = 1 to nrow(u)-1;     /* for each group... */
      idx = u[i]:(u[i+1]-1);  /* get rows in group */
      y = z[idx,2];           /* extract data for this BY group */
      /* perform computations on this BY group */
      q = quartile(y);
   end;
end;
result[k,3] = (time() - t0)/NReps; /* time for UniqueBy */
 
end;  /* end of k loop */
print result[c={'NumGroups' 'Time Unique-Loc' 'Time UniqueBY'} F=Best5.];
 
create Results from result[c={'NumGroups' 'tUniqueLoc' 'tUniqueBy'}];
append from result;
close;
 
QUIT;
title "Performance of UNIQUE-LOC vs UNIQUEBY Processing";
title2 "500,000 Observations";
proc sgplot data=Results;
   series x=NumGroups y=tUniqueLoc / curvelabel='Unique-Loc';
   series x=NumGroups y=tUniqueBy / curvelabel='UniqueBy';
   xaxis grid label="Number of Groups";
   yaxis grid label="Time (s)";
run;