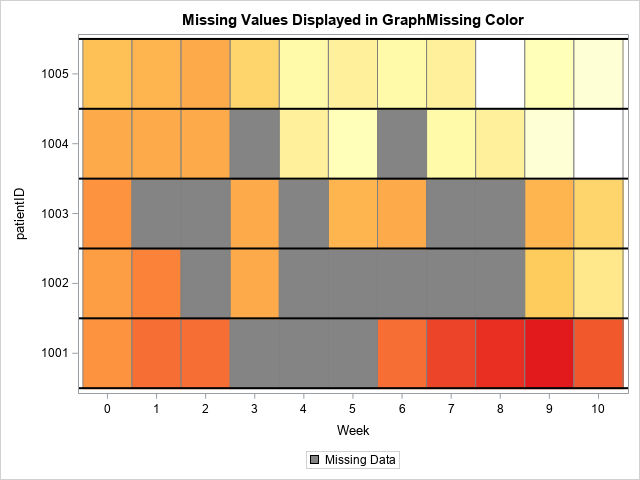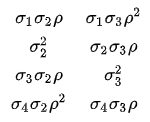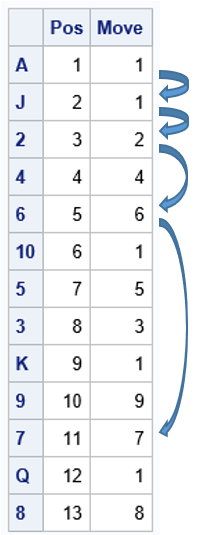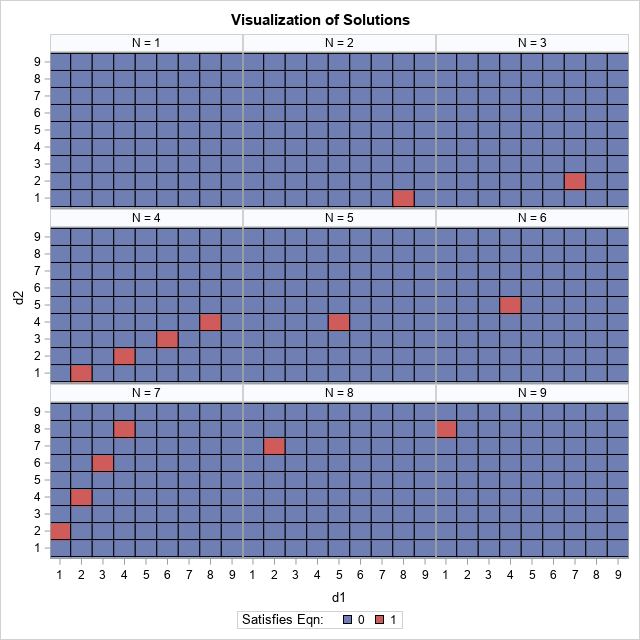
I recently discussed introductory programming with a colleague who teaches Python at a university. He told me about the following introductory programming assignment: Let N be an integer parameter in the range [1, 9]. For each value of N, find all pairs of one-digit positive integers d1 and d2 that