Happy Pi Day! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate "all things pi-related" because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979....

Modern computer methods and algorithms enable us to calculate 100 trillion digits of π. However, I think it is fascinating to learn about how mathematicians in the pre-computer age were able to approximate π to many decimal places through cleverness and manual paper-and-pencil calculations.

One of best mathematicians of all time was Isaac Newton, who calculated 16 digits of π by hand way back in 1666. Newton accomplished this by combining geometry with several mathematical techniques that were new at the time. These techniques included the new field of integral calculus (which Newton himself invented), and an early use of a truncated infinite series to approximate a function. Newton's formulation of the problem is understandable by any high-school geometry student. Although the manual calculations are tedious, they can be understood by anyone who has taken calculus. In this article, I use a computer to simplify the long calculations in Newton's approximation. The computer calculation avoids the infinite series and provides a 14-decimal approximation to π.

I learned about Newton's approximation from Matt Parker and the "Think Maths" group in the UK, who made a wonderful video about Newton's approximation. They also provide resources for math teachers who want to present this topic to their students.

The geometry of Newton's calculation

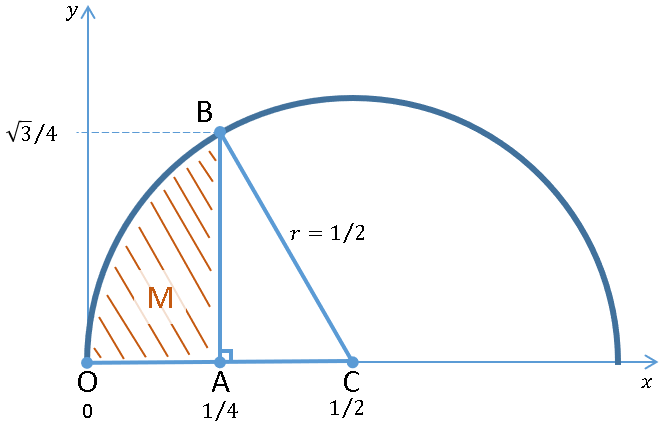
The figure at the right shows the geometry behind Newton's calculation of pi. First, draw a semicircle of radius 1/2 centered at the point C(1/2, 0) in the Cartesian plane. Then draw a vertical line segment from A(1/4, 0) until it hits the circle at B. High school geometry shows that the triangle ABC is a 30-60-90 triangle, and the line segment AB intersects the circle at B(1/4, sqrt(3)/4).

Newton knew the following facts:

1. The angle OCB is 60 degrees. Therefore, the area of the sector OCB is π/6 r², where r is the radius of the circle. Because the radius is r = 1/2, the area of the sector OCB is π / 24.
2. The area of the triangle ABC is easily found to be (1/2)*base*height = (1/2)(1/4)(sqrt(3)/4) = sqrt(3)/32. Newton could calculate this quantity to an arbitrary number of decimal places because the square root algorithm was known by the ancient Babylonians and by the Greeks.
3. The area of the crosshatched region (denoted M) can be found by calculating a definite integral. The equation of the semicircle is $f(x) = \sqrt{\tfrac{1}{4} - (x-\tfrac{1}{2})^2}$, which simplifies to $f(x) = \sqrt{x} \sqrt{1-x}$. Therefore, the area can be calculated as $M = \int_0^{1/4} \sqrt{x} \sqrt{1-x} \, dx$.

From the figure, we see that Area(OCB) = M + Area(ABC). Plugging in the formulas for these quantities, we get
π /24 = M + sqrt(3)/32. Multiplying both sides by 24 gives the equation that Newton used to approximate π:
      π = 24*M + 3 sqrt(3)/4

Newton approximated M to many decimal places, thus providing a decimal approximation for π. Newton used a truncated infinite series expansion to approximate M, but the next section shows an alternative approach: you can use numerical integration to approximate M.

A modern version of Newton's approximation

By using modern computational techniques, you can evaluate the integral (M) numerically. If you evaluate M to high precision, you get a high-precision approximation for π.

Most modern computer languages include a function to evaluate a definite integral on a closed interval. The SAS/IML language provides the QUAD subroutine, which enables you to compute M to many decimal digits by using numerical quadrature (integration). Here is the SAS/IML program that carries out Newton's approximation of pi:

/* Newton's approximation of pi. For details, see https://think-maths.co.uk/newton-pi */
proc iml;
/* integrand is f(x) = sqrt(0.25 - (x-0.5)##2)
                     = sqrt(x*(1-x)) */
start SemiCircle(x);
   return( sqrt(x - x##2) );
finish;
 
/* numerical approximation of M = area under semicircle on [0, 1/4] */
call quad(M, "SemiCircle", {0, 0.25}) EPS=1E-15;
 
/* AreaSector = pi/6 * r^2 = pi / 24 
   Newton used AreaSector = M + AreaTri, so
     pi / 24 = M + AreaTri
     pi = 24*(M + AreaTri)
*/
AreaTri = 1/2 * (1/4) * (sqrt(3) / 4); /* area of triangle ABC */
piApprox = 24*(M + AreaTri);
print piApprox[F=16.14 L="Newton's Approx"];

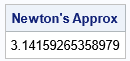
The program outputs an approximation to pi that is accurate to 14 decimal digits. This value is the standard double-precision floating-point approximation to pi. The program gives the same result as the SAS function constant('pi').

Newton's approximation by using infinite series

Notice that my approximation only captures the value of pi to 14 decimal digits, whereas Newton achieved 16-digit accuracy. How did Newton get more accuracy? He didn't use a numerical method for integrating the integral. Instead, he used the binomial expansion of the term sqrt(1 - x), which replaces the term by an infinite series. He kept 22 terms of the infinite series and integrated (by hand!) the resulting expression.

I am not going to repeat Newton's tour de force calculation, but you can watch a video in which the Think Maths group in the UK repeats Newton's calculation by hand using long division and extremely large pieces of paper! The group also created a document that shows the details. The main idea is to recall the binomial expansion:
$(1+z)^{\frac {1}{2}} = 1 +{\tfrac {1}{2}}z -{\tfrac {1}{8}}z^{2} +{\tfrac {1}{16}}z^{3} -{\tfrac {5}{128}}z^{4} +{\tfrac {7}{256}}z^{5} -\cdots = \sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n!)^{2}(2n-1)}}z^{n}$

In this case, we want to replace z by (-x), which changes the sign of terms that contain odd powers of z. The result is an infinite series in which each term (except the first) has a negative sign:

Newton kept 22 terms of this infinite series and integrated the function term-by-term on the interval [0, 1/4]. The result is 22 fractions that can be evaluated by long division. However, the numerator and denominator of the higher-order terms are HUGE! For example, the 20th term is the fraction 119,409,675 / (41*2⁷⁵). Although, in principle, you could calculate Newton's approximation by hand (and, remember, he did!), it would not be a pleasant way to spend an evening.

Summary

In 1666, Newton computed 16 digits of π by constructing a geometric figure in which the value of pi is related to the numerical approximation of an integral. Newton approximated the integral by expanding a function in an infinite series, truncating the series at 22 terms, and evaluating each term by using long division. Although the formulation and general idea is accessible to calculus students, the calculations are long and tedious. Instead, you can use modern numerical methods to evaluate the integral, thus computing a 14-digit approximation to π.

References

• Matt Parker, "Newton's Approximation for pi," video accessed 03MAR2023.
• Think Maths, "Teacher Notes and Solutions" for "Newton's Approximation for pi." A fully worked explanation of how Newton approximated pi to 16 decimal places in 1666.