When I encounter a new function, I usually graph it to gain intuition about how the function transforms its inputs. Recently, I needed to use the Rayleigh quotient function, which is connected to the estimation of eigenvalues and eigenvectors for symmetric matrices. It has been several years since I last
The new school year had barely started when I got a call from a friend who is an elementary school principal. She told me that every morning she announces the names of students who are celebrating a birthday. "One student noticed that we've already had two days on which no
In probability and statistics, special numbers are used to compute probabilities by counting the number of ways certain events can occur. The most famous are combinations and permutations. Both are used to count the ways to arrange or select items from a set. If a set contains n elements: A
SAS provides procedures to fit common probability distributions to sample data. You can use PROC UNIVARIATE in Base SAS or PROC SEVERITY in SAS/ETS software to estimate the distribution parameters for approximately 20 common distributions, including normal, lognormal, beta, gamma, and Weibull. Since there are infinitely many distributions, you may
Many common probability distributions contain terms that increase or decrease quickly, such as the exponential function and factorials. The numerical evaluation of these quantities can result in numerical overflow (or underflow). This is why we often work on the logarithmic scale: on the log-scale, the numerical computations for equations such
Isaac Newton had many amazing scientific and mathematical accomplishments. His law of universal gravitation and his creation of calculus are at the top of the list! But in the field of numerical analysis, "Newton's Method" was a groundbreaking advancement for solving for a root of a nonlinear smooth function. The
Newton's method was in the news this week. Not the well-known linear method for finding roots, but a more complicated method for finding minima, sometimes called the method of successive parabolic approximations. Newton's parabolic method was recently improved by modern researchers who extended the method to use higher-dimensional polynomials. The
A previous article describes how to use SAS to find the inflection points of a 1-D function that you can evaluate at any point. The function must be given by a formula (or by an algorithm) because the root-finding algorithm needs to evaluate the function at arbitrary locations. However, sometimes
A SAS programmer asked if it is possible to numerically find an inflection point for a univariate function, f(x). Yes! This can be solved as a variation of a classic numerical root-finding problem. Recall that an inflection point is a value (call it x0) in the domain where the graph
I previously wrote an article about the Lambert W function. The Lambert W function is the inverse of the function g(x) = x exp(x). This means that you can use it to find the value of x such that g(x)=c for any value of c in the range of g, which
A SAS programmer had many polynomials for which he wanted to compute the real roots. By the Fundamental Theorem of Algebra, every polynomial of degree d has d complex roots. You can find these complex roots by using the POLYROOT function in SAS IML. The programmer only wanted to output
A colleague asked me an interesting question: Suppose you have a structured correlation matrix, such as a matrix that has a compound symmetric, banded, or an AR1(ρ) structure. If you generate a random correlation matrix that has the same eigenvalues as the structured matrix, does the random matrix have the
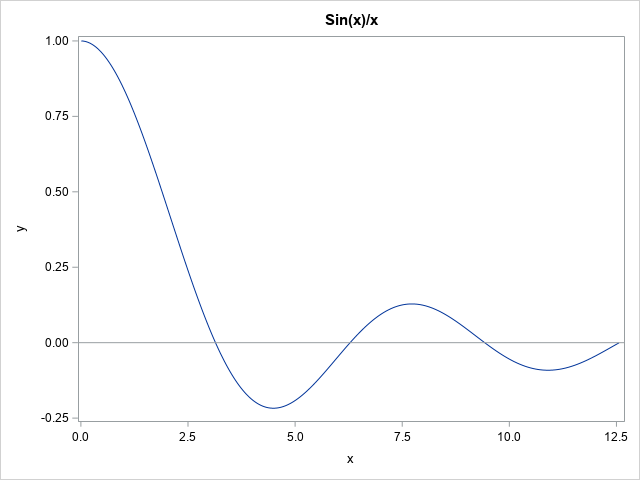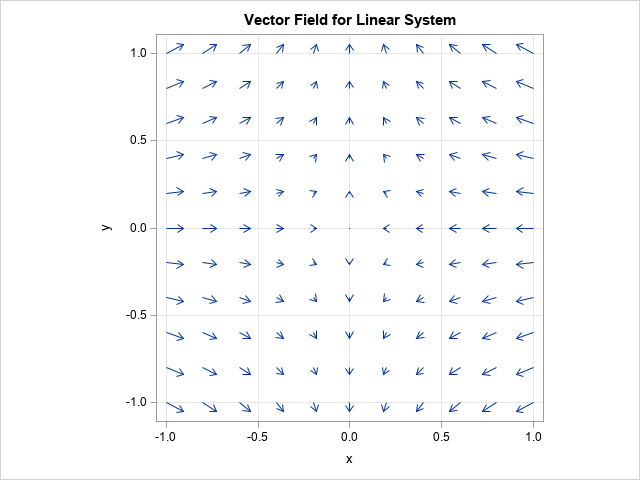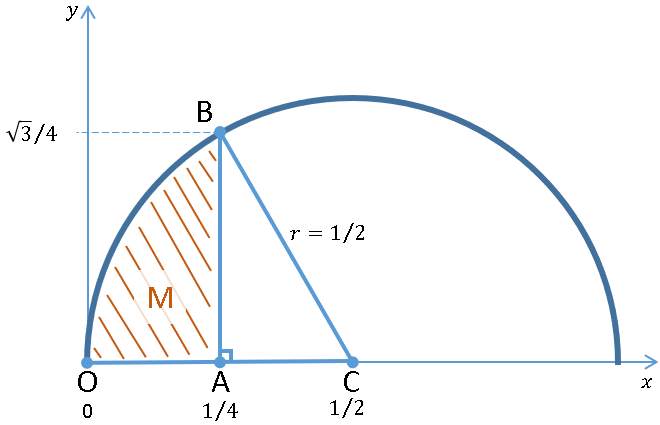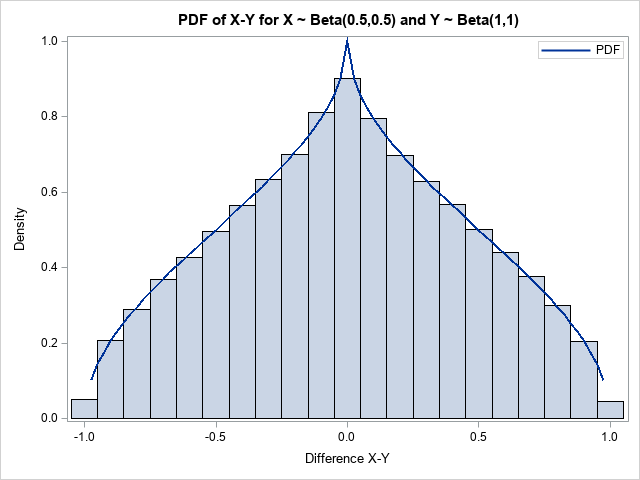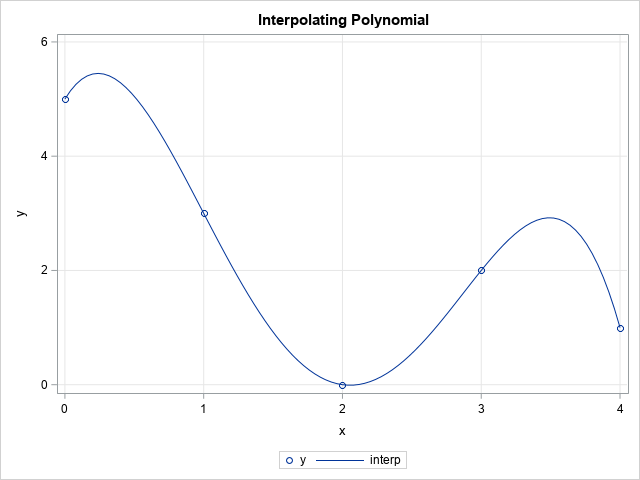
While reviewing a book on numerical analysis, I was reminded of a classic interpolation problem. Suppose you have n pairs of points in the plane: (x1,y1), (x2,y2), ..., (xn,yn), where the first coordinates are distinct. Then you can construct a unique polynomial of degree (at most) n-1 that passes through
A SAS programmer wanted to simulate samples from a family of Beta(a,b) distributions for a simulation study. (Recall that a Beta random variable is bounded with values in the range [0,1].) She wanted to choose the parameters such that the skewness and kurtosis of the distributions varied over range of
I read a journal article in which a researcher used a formula for the probability density function (PDF) of the sample correlation coefficient. The formula was rather complicated, and presented with no citation, so I was curious to learn more. I found the distribution for the correlation coefficient in the
A colleague remarked that my recent article about using Jacobi's iterative method for solving a linear system of equations "seems like magic." Specifically, it seems like magic that you can solve a certain class of linear systems by using only matrix multiplication. For any initial guess, the iteration converges to
In a first course in numerical analysis, students often encounter a simple iterative method for solving a linear system of equations, known as Jacobi's method (or Jacobi's iterative method). Although Jacobi's method is not used much in practice, it is introduced because it is easy to explain, easy to implement,
The collinearity problem is to determine whether three points in the plane lie along a straight line. You can solve this problem by using middle-school algebra. An algebraic solution requires three steps. First, name the points: p, q, and r. Second, find the parametric equation for the line that passes
A previous article shows how to use Monte Carlo simulation to approximate the sampling distribution of the sample mean and sample median. When x ~ N(0,1) are normal data, the sample mean is also normal, and there are simple formulas for the expected value and the standard error of the
Recently I wrote about numerical analysis problem: the accurate computation of log(1+x) when x is close to 0. A naive computation of log(1+x) loses accuracy if you call the LOG function, which is why the SAS language provides the built-in LOG1PX for this computation. In addition, I showed that you
SAS supports a special function for the accurate evaluation of log(1+x) when x is near 0. The LOG1PX function is useful because a naive computation of log(1+x) loses accuracy when x is near 0. This article demonstrates two general approximation techniques that are often used in numerical analysis: the Taylor
The other day I was trying to numerically integrate the function f(x) = sin(x)/x on the domain [0,∞). The graph of this function is shown to the right. In SAS, you can use the QUAD subroutine in SAS IML software to perform numerical integration. Some numerical integrators have difficulty computing
In SAS, you can approximate the exponential of a matrix by using the EXPMATRIX function in SAS IML software. This article discusses the exponential of a matrix: what it is, how to compute it, why it is useful, and why you should think of it as a linear map that
Happy Pi Day! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate "all things pi-related" because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979.... Modern computer methods and algorithms enable us to calculate 100 trillion digits of π. However, I think it
A SAS programmer wanted to compute the distribution of X-Y, where X and Y are two beta-distributed random variables. Pham-Gia and Turkkan (1993) derive a formula for the PDF of this distribution. Unfortunately, the PDF involves evaluating a two-dimensional generalized hypergeometric function, which is not available in all programming languages.
In applied mathematics, there is a large collection of "special functions." These function appera in certain applications, often as the solution to a differential equation, but also in the definition of probability distributions. For example, I have written about Bessel functions, the complete and incomplete gamma function, and the complete
Monotonic transformations occur frequently in math and statistics. Analysts use monotonic transformations to transform variable values, with Tukey's ladder of transformations and the Box-Cox transformations being familiar examples. Monotonic distributions figure prominently in probability theory because the cumulative distribution is a monotonic increasing function. For a continuous distribution that is
A colleague was struggling to compute a right-tail probability for a distribution. Recall that the cumulative distribution function (CDF) is defined as a left-tail probability. For a continuous random variable, X, with density function f, the CDF at the value x is F(x) = Pr(X ≤ x) = ∫
Recently, I needed to solve an optimization problem in which the objective function included a term that involved the quantile function (inverse CDF) of the t distribution, which is shown to the right for DF=5 degrees of freedom. I casually remarked to my colleague that the optimizer would have to
To a numerical analyst, numerical integration has two meanings. Numerical integration often means solving a definite integral such as $$int_{a}^b f(s) , ds$$. Numerical integration is also called quadrature because it computes areas. The other meaning applies to solving ordinary differential equations (ODEs). My article about new methods for solving
