It is important to be able to detect whether a numerical matrix is symmetric. Some operations in linear algebra require symmetric matrices. Sometimes, you can use special algorithms to factor a symmetric matrix. In both cases, you need to test a matrix for symmetry.

A symmetric matrix must be square. Mathematically, we say that an n x n matrix, A, is symmetric if A = A^T. In terms of the elements of A, the matrix is symmetric if A[i,j] = A[j,i] for all 1 < i < j ≤ n.

How to test a numerical matrix for symmetry

In numerical linear algebra, you should usually avoid testing floating-point numbers for equality. Instead, ask whether the difference | A[i,j] - A[j,i] | is smaller than some value, δ. But what small value should you choose for δ? Although a value such as δ = 1E-14 is suitable for many matrices, symmetry should not depend on the scaling of the matrix. In other words, the test for the matrices A and k*A should give the same results for any nonzero scalar, k.

One way to ensure that the scale of the matrix does not affect the result is to operate on a standardized matrix. You can use the elements of A to determine the scale factor. Let c = max(|A[i,j]|) for 1 ≤ i, j ≤ n. Define δ = c*sqrt(ε), where ε is machine precision. In SAS, you can use the CONSTANT('MACEPS') and CONSTANT('SQRTMACEPS') function calls to obtain the value of ε and sqrt(ε), respectively. SAS uses 2.22E-16 for machine precision, so sqrt(ε) ≈ 1.5e-8.

In summary, a good test for symmetry is to test whether all pairwise differences satisfy the equation | A[i,j] - A[j,i] | < c*sqrt(ε), where c = max(|A[i,j]|). This is equivalent to scaling A so that the largest element has unit magnitude and comparing the scaled differences with sqrt(ε).

In a matrix language such as SAS/IML, you can easily write a function that tests for symmetry, as follows:

proc iml;
 
start TestSym(A);
   if nrow(A) ^= ncol(A) then return(0);    /* A is not square */
   c = max(abs(A));
   sqrteps = constant('SqrtMacEps');
   return( all( abs(A-A`) < c*sqrteps ) );
finish;

Examples of testing a matric for symmetry

With that definition, let's see whether the function works on a few example matrices. The first example is a symmetric matrix. Let's see whether the test returns 1 (true) for the matrix and for various scalings of the matrix:

/* A is symmetric. TestSym(A) should return 1 (true). */
A = {1  2  3 -4  5,
     2  3  2  3  3,
     3  2  5 -1  0,
    -4  3 -1  4 -2, 
     5  3  0 -2  1 };
b1 = TestSym(A);
b2 = TestSym(1E6 * A);
b3 = TestSym(1E-8 * A);
print b1 b2 b3;

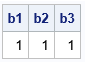
Success. The TestSym function correctly detects that the matrix is symmetric. Various scalings of the matrix are also deemed symmetric.

What happens if we break the symmetry by making a tiny change to the (3,5) element?

/* break the symmetry by changing an off-diagonal element */
A[3,5] = 1e-6;
d1 = TestSym(A);
d2 = TestSym(1E6 * A);
d3 = TestSym(1E-8 * A);
print d1 d2 d3;

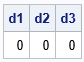
For this matrix, the magnitude of the largest element is c=5. The perturbation to the matrix is 1e-6, which is less than c*sqrt(ε). Accordingly, the test detects that the perturbed matrix and its scalings are not symmetric. If you rerun the previous statements but use a smaller perturbation such as A[3,5] = 1e-9, the test will declare that the matrix is "numerically symmetric." Tiny differences between A[i,j] and A[j,i] are ignored, where "tiny" is relative to the magnitude of the largest element of A.

Make a symmetric matrix

There are times when you might want to form a matrix that is symmetric from a matrix that is nearly symmetric. An easy way to do that is to use the matrix B = (A + A^T)/2, as follows:

B = (A + A`)/2;      /* B is always symmetric */
isSym = TestSym(B);
print isSym;

For any square matrix, A, the matrix B = (A + A^T)/2 is symmetric. I call the matrix B the symmetricization of A. An off-diagonal elements B[i,j] is the average of the corresponding elements A[i,j] and A[j,i].

Summary

This article shows how to test a matrix for symmetry in numerical linear algebra. It uses the largest value of the matrix as a scale factor to standardize the computation. This technique is used in several SAS/IML functions that need to determine whether a matrix is symmetric.

Test for skew symmetric matrix

Here is an exercise for the motivated reader. A square matrix, M, is skew-symmetric if it satisfies the equation M = -M`. In other words, M[i,j] = -M[j,i] for all 1 < i, j ≤ n. Can you modify the TestSym function to test a matrix for a skew-symmetry to within some numerical precision? Hint: You only need to change one line!