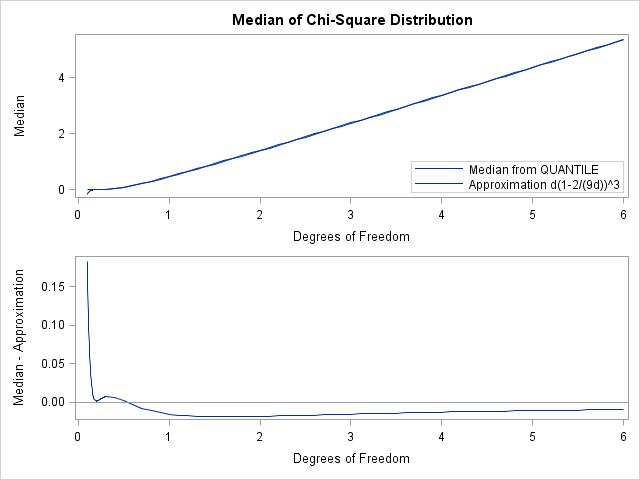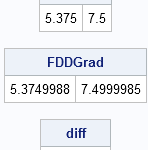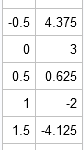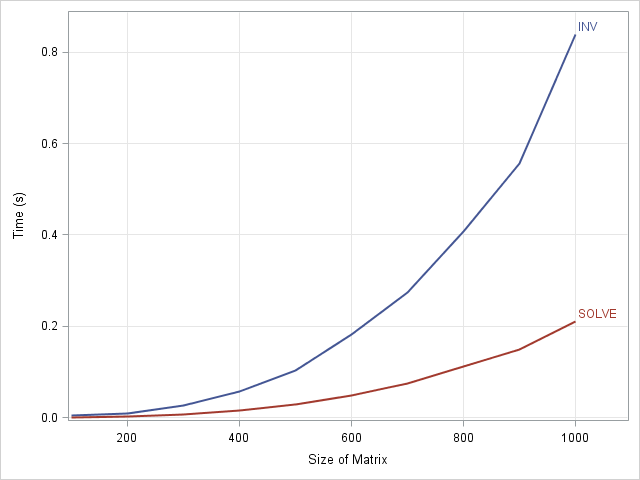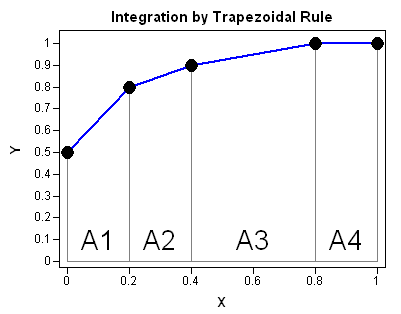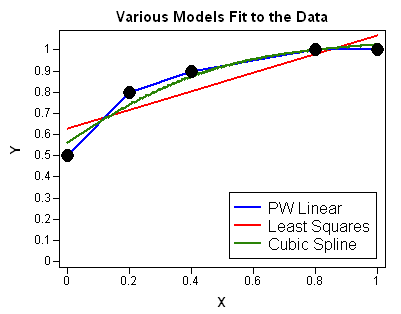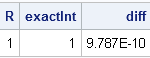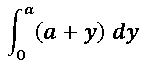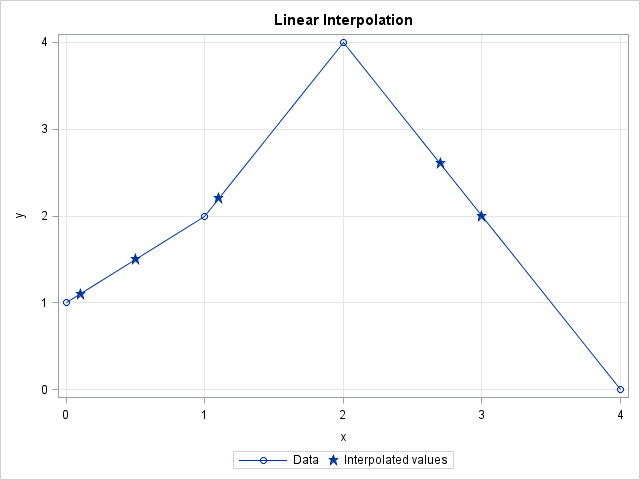
A recent discussion on the SAS-L discussion forum concerned how to implement linear interpolation in SAS. Some people suggested using PROC EXPAND in SAS/ETS software, whereas others proposed a DATA step solution. For me, the SAS/IML language provides a natural programming environment to implement an interpolation scheme. It also provides
I was at the Wikipedia site the other day, looking up properties of the Chi-square distribution. I noticed that the formula for the median of the chi-square distribution with d degrees of freedom is given as ≈ d(1-2/(9d))3. However, there is no mention of how well this formula approximates the
I previously wrote about using SAS/IML for nonlinear optimization, and demonstrated optimization by maximizing a likelihood function. Many well-known optimization algorithms require derivative information during the optimization, including the conjugate gradient method (implemented in the NLPCG subroutine) and the Newton-Raphson method (implemented in the NLPNRA method). You should specify analytic
Polynomials are used often in data analysis. Low-order polynomials are used in regression to model the relationship between variables. Polynomials are used in numerical analysis for numerical integration and Taylor series approximations. It is therefore important to be able to evaluate polynomials in an efficient manner. My favorite evaluation technique
I've previously described ways to solve systems of linear equations, A*b = c. While discussing the relative merits of the solving a system for a particular right hand side versus solving for the inverse matrix, I made the assertion that it is faster to solve a particular system than it
The SAS/IML language provides two functions for solving a nonsingular nxn linear system A*x = c: The INV function numerically computes the inverse matrix, A-1. You can use this to solve for x: Ainv = inv(A); x = Ainv*c;. The SOLVE function numerically computes the particular solution, x, for a
I've previously discussed how to find the root of a univariate function. This article describes how to find the root (zero) of a function of several variables by using Newton's method. There have been many papers, books, and dissertations written on the topic of root-finding, so why am I blogging
At the SAS/IML Support Community, a SAS/IML programmer recently asked how to find "the root of a complicated equation." That's a huge question, and many papers and books have been written on the topic of root-finding, also known as finding the zeros of a function. Everyone has favorite techniques for
In a previous blog post, I presented a short SAS/IML function module that implements the trapezoidal rule. The trapezoidal rule is a numerical integration scheme that gives the integral of a piecewise linear function that passes through a given set of points. This article demonstrates an application of using the
In a previous article I discussed the situation where you have a sequence of (x,y) points and you want to find the area under the curve that is defined by those points. I pointed out that usually you need to use statistical modeling before it makes sense to compute the
The other day I was asked, "Given a set of points, what is the area under the curve defined by those points?" As stated, the problem is not well defined. The problem is that "the curve defined by those points" doesn't have a precise meaning. However, after gathering more information,
This blog post shows how to numerically integrate a one-dimensional function by using the QUAD subroutine in SAS/IML software. The name "quad" is short for quadrature, which means numerical integration. You can use the QUAD subroutine to numerically find the definite integral of a function on a finite, semi-infinite, or
The SAS/IML language provides the QUAD function for evaluating one-dimensional integrals. You can also use the QUAD function to compute a double integral as an iterated integral. A One-Dimensional Integration Suppose you want to evaluate the following integral: To evaluate this integral in the SAS/IML language: Define a function module
