Many experienced SAS programmers use the PUT statement to write messages to the log from a DATA step. But did you know that SAS supports the PUTLOG function, which is another way to write a message to the log? I use the PUTLOG statement in the DATA step for the following reasons:

• It is easy to understand. The name of the statement alerts anyone reading the program that the program is sending a message to the log.
• It is specific. Whereas the PUT statement can be used to write to any open file, the PUTLOG statement always writes to the log.
• It is dependable. Suppose you are writing a SAS macro that other people will use. If you use the PUTLOG statement, your message will always appear in the log. If you use the PUT statement, you have to handle the possibility that the user has defined a fileref, which could potentially redirect the messages away from the log.
• It displays colored messages: f you start the message with the keywords "NOTE:", "WARNING:", or "ERROR", the log displays the message in a special color.

How to use the PUTLOG statement

The PUTLOG statement is easy to use. Typically, it is part of an IF-THEN block and is executed conditionally when a certain condition is encountered. You can display a message in the log, but you can also display the values of any variables in the DATA step.

The following DATA step reads in coefficients for a quadratic equation a x² + b x + 3 = 0. For each set of coefficients, the program uses the discriminant of the quadratic equation to determine whether the equation has any real roots. If so, the program uses the quadratic formula to find the roots. To demonstrate the three common log messages, the program does the following:

• Display an ERROR if the coefficient of the quadratic term is 0.
• Display a WARNING if the quadratic equation does not have any real roots.
• Display a NOTE if the quadratic equation does has a repeated root.

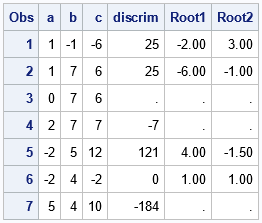
/* Read coefficients of quadratic equation a*x**2 + b*x + c.
   For a ^= 0, use the quadratic formula to solve for real roots of
   a*x**2 + b*x + c = 0.
*/
data Quadratic;
input a b c;
if a=0 then 
   putlog "ERROR: The coefficient of the quadratic term is 0 for observation " _N_;
else do;
   discrim = b**2 - 4*a*c;
   if discrim < 0 then do;
      putlog "WARNING: No real roots for observation " _N_
             "; the coefficients are " a= b= c=;
      Root1 = .; Root2 = .;
   end;
   else do;
      Root1 = (-b - sqrt(discrim)) / (2*a);
      Root2 = (-b + sqrt(discrim)) / (2*a);
      if Discrim=0 then 
         putlog "NOTE: Repeated root for observation " _N_;
   end;
end;
datalines;
 1 -1 -6
 1  7  6
 0  7  6
 2  7  7
-2  5 12
-2  4 -2
 5  4 10
;
 
proc print; format Root1 Root2 5.2; run;

The SAS log contains the following message, which is color-coded according to whether the message is an error (red color), a warning (green color), or a note (blue color).

The output from the PRINT procedure shows the results of the DATA step. For coefficients that have real roots, the Root1 and Root2 columns show the roots. If the equation is not quadratic or has no real roots, the columns show missing values. Notice that there are missing values for observations 3, 4, and 7, which are the observations that are mentioned in the log messages.

Summary

The PUTLOG statement is an easy way to write messages to the log from a SAS DATA step. You can use the PUTLOG statement to display messages when the data is unusual, and a computation cannot be completed.

In closing, I want to mention that outside of a DATA step, you can use the %PUT statement to write a message to the log. Like the PUTLOG statement, the message will be color-coded if you begin the message with "NOTE:", "WARNING:", or "ERROR:".