In a previous article, I presented some of the most popular blog posts from 2022. In general, popular articles deal with elementary topics that have broad appeal. However, I also write articles about advanced topics. The following articles didn't make the Top 10 list, but they deserve a second look. I have grouped them into four categories: statistics, simulation and bootstrapping, visualization and ODS, and numerical analysis and matrix computations.

Statistics and data analysis

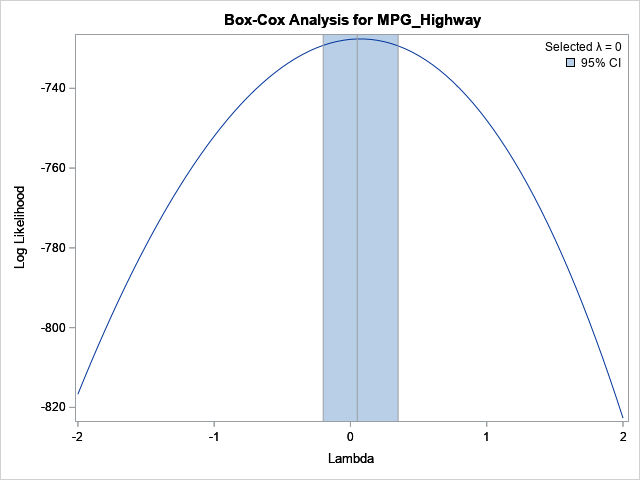
• Box-Cox Transformations: An assumption of least squares regression is that the residuals for the models are normally distributed. If they are not, some researchers try to apply a nonlinear transformation to the dependent (Y) variable to normalize the residuals. But what transformation should you use? The Box-Cox transformation is a process that picks a power transformation that is interpretable and that best normalizes the residuals. You can use the same process to perform a transformation that best normalizes a single variable. In SAS, you can use PROC TRANSREG to perform Box-Cox transformations and to visualize the process.
• Partial regression leverage plots: PROC REG can create partial regression leverage plots. What are they and how do you interpret the plots? A partial regression leverage plot visualizes the parameter estimates and the null hypothesis β_i=0 for each effect in the model. It also enables you to see outliers and high-leverage points for each regressor. You can also add a confidence limit for the test of the null hypothesis to the plot.

Simulation and bootstrapping

• How often do statistical tests agree?: A SAS programmer noticed that SAS supplied two statistical tests for the same null hypothesis. One of the tests rejected the null hypothesis whereas the other one failed to reject it. A simulation study can help you understand how often this situation occurs, and how you can interpret this situation.
• Bootstrap estimates for nonlinear regression: For linear least squares regression, there are asymptotic formulas for the confidence intervals for parameters. No formulas exist for a general nonlinear regression, but you can use bootstrapping to obtain confidence intervals for the regression parameters and their covariance. The BOOTSTRAP statement in PROC NLIN makes it easy to obtain a bootstrap confidence interval for the regression parameters in a nonlinear regression model.
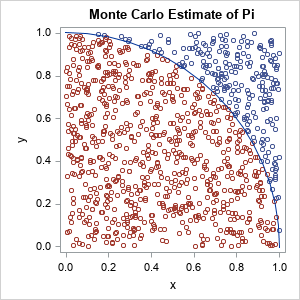
• Introductory examples of Monte Carlo simulation in SAS: If you've ever thought about learning how to perform Monte Carlo simulation in SAS, this article collects 10 classic Monte Carlo examples that do not require any advanced knowledge of probability or statistics. As such, these problems are ideal for beginning learners.

Data visualization and ODS

• Create a panel of graphs: Often SAS programmers ask how to create a panel of graphs. When the graphs are the same type, you can often use PROC SGPANEL to create a grid of graphs. But sometimes the two graphs are created by using two different procedures, and you want to display them side by side. This article shows how to select the graphs and arrange them side-by-side by using the ODS LAYOUT GRIDDED statement.



• PUSH and POP ODS states: Did you know that the ODS GRAPHICS statement supports 30 options that enable you to configure the attributes of graphs that you create in SAS? Did you know that you can temporarily set certain options and then restore the options to their previous values? This article shows how to use the SHOW, PUSH, POP, and RESET options on the ODS GRAPHICS statement.
• ODS select list for destinations: Do you know how to inspect the ODS SELECT list for all open ODS destinations? The tips in this article ensure that you know which output will appear in which destinations.

Numerical analysis and matrix computations

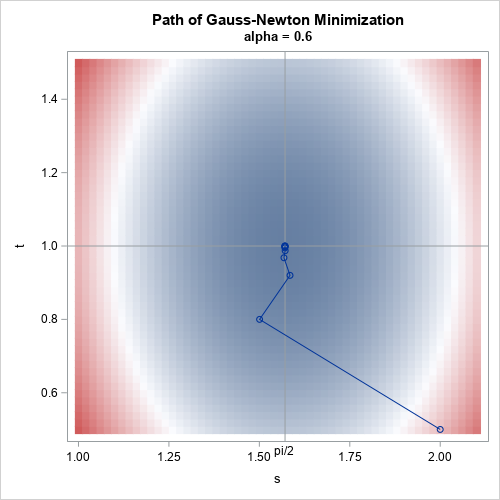
• Least squares optimization: Many SAS/IML programmers use the built-in optimization routines to find a local minimum or local maximum for a scalar-valued function. But not everyone knows that you can also find the least-square minimum of a vector-valued function. This article discusses the process and provides an example.
• Finite-difference derivatives: The SAS/IML language supports routines that compute finite-difference derivatives. For scalar-valued functions, these routines approximate the gradient and the Hessian (vector of first derivatives and matrix of second derivatives) at a specified point. For vector-valued functions, the routines approximate the Jacobian matrix at a specified point.
• New solver for ordinary differential equations: SAS Viya is the future of SAS. Although SAS/IML in SAS 9.4 supports an ODE solver, SAS IML software in Viya supports the new ODEQN subroutine, which solves ODEs that are initial value problems by using state-of-the-art numerical algorithms. This article describes the advantages of the new methods and provides examples.
• Solve rank-deficient systems of equations: In some applications, you can encounter an overdetermined system of linear equations. In this event, the system usually has infinitely many solutions. You might want to detect that the system is singular and return a special solution: the one that has the smallest L₂ norm. This article discusses how to detect and solve a rank-deficient system of equations in the SAS IML language.

Your turn

Did I omit one of your favorite blog posts from The DO Loop in 2022? Maybe you liked my heart-shaped billiard table for Valentine's Day? Of maybe you enjoyed my Pi Day article about the π^th roots of unity? If so, leave a comment and tell me what topic you found interesting or useful.