A previous article describes how to use SAS IML software to construct common covariance structures that are encountered in mixed models. Each covariance matrix has several parameters, and you want to construct a matrix for any choice of the parameters. After you have constructed the covariance matrix, you can use the RandNormal function in SAS IML to generate random variates from a multivariate normal distribution that is defined by the covariance matrix. This is one step in a simulation that generates data from a mixed-effect regression model.

Over the years, SAS has added many covariance matrices to PROC MIXED. The procedure can now model close to 40 different covariance structures. Some of the matrix definitions are complicated to define. The PROC MIXED documentation displays formulas for each structure, but I think the better way to view these matrix structures is to look at the pattern of the cells in terms of the parameters. Often you can represent a complicated matrix as the sum, Hadamard product, or direct product of simpler matrices.

This article shows how to construct several covariance matrices that exhibit "heterogeneous structure."

Structured covariance matrices

The documentation for the REPEATED statement in PROC MIXED displays about 40 covariance structures for each subject in a repeated-measures mixed model. The following matrix structures were discussed previously:

• Wicklin (2012) presents several R-side covariance structures, including variance components (diagonal), compound symmetric, Toeplitz (banded), and AR(1) structured matrices.
• Gibbs and Kiernan (2020) presents compound symmetric and AR(1) structures for R-side errors, but also discusses simulation of G-side random effects.

The following sections show how to construct a few other matrices that are listed in the PROC MIXED documentation.

Heterogeneous structures

Several structures contain the word "heterogeneous" in their name. These heterogeneous structures are the Hadamard product of an outer-product matrix and another structured matrix. The heterogeneous structures include the following:

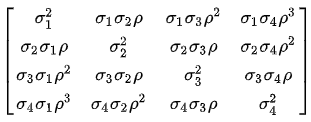
• Heterogeneous AR(1), which is also called ARH(1)
• Heterogeneous compound symmetry, which is represented as CSH
• Heterogeneous Toeplitz (TOEPH)
• Banded heterogeneous Toeplitz
• First-order antedependence, which is also called ANTE(1)

For example, a mathematical representation of an ARH(1) structure is shown. Notice that each cell has a term that looks like $\sigma_i \sigma_j$. Those quantities are formed as the outer product $\boldsymbol{\sigma} \boldsymbol{\sigma}^\prime$, where $\boldsymbol{\sigma} = (\sigma_1, \sigma_2, \sigma_3, \sigma_4)$ for this matrix.

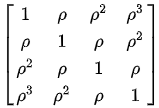
To create a heterogeneous structure, first construct the outer-product matrix. Then construct another matrix, such as an AR(1), CS, or Toeplitz. For example, a mathematical representation of an AR(1) correlation structure is shown to the right. An AR(1) correlation struture is an example of a Toeplitz matrix for which the generating vector is $(1, \rho, \rho^2, \ldots, \rho^d)$.

The heterogeneous structure is the Hadamard product of the two matrices. This is shown in the following SAS IML program for the heterogeneous AR(1) structure:

proc iml;
/* AR1 correlation structure:
   https://blogs.sas.com/content/iml/2012/11/05/constructing-common-covariance-structures.html */
start AR1Corr(dim, rho);
   u = cuprod(j(1,dim-1,rho)); /* cumulative product */
   return( toeplitz(1 || u) );
finish;
 
/* construct ARH(1) heterogeneous structure as Hadamard product 
   of outer-produt matrix (sigma*sigma`) and an AR(1) matrix */
sigma = {2, 4, 3, 1};
rho=0.5;                     /* AR(1) parameter */
dim = nrow(sigma);
 
OutProd = sigma * sigma`;
AR1 = AR1Corr(dim, rho);
ARH1Cov = OutProd # AR1;     /* Hadamard product */
print OutProd, AR1, ARH1Cov;

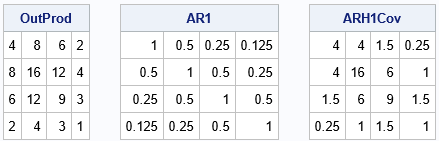
The output shows the three matrices. The first matrix is an outer product of a vector that contains four standard deviation parameters. The second matrix is an AR(1) covariance matrix with the parameter ρ = 1/2. The third matrix is the Hadamard product (elementwise multiplication) of the first two matrices. The third matrix exhibits the heterogeneous AR(1) structure, which is also called the ARH(1) structure.

You can use the same process to construct other heterogeneous structures. The first step is always the same. You change the structure of the second matrix.

Summary

This article shows how to construct a heterogeneous structured covariance matrix. Examples include heterogeneous AR(1), heterogeneous compound symmetry (CSH), heterogeneous Toeplitz (TOEPH), and first-order antedependence (ANTE(1)). The heterogeneous matrices are Hadamard products of an outer-product matrix and another structured matrix. The SAS IML language supports functions and operations that make it easy to construct these matrices.