A probabilistic card trick is a trick that succeeds with high probability and does not require any skill from the person performing the trick. I have seen a certain trick mentioned several times on social media. I call it "ladders" or the "ladders game" because it reminds me of the childhood board game Chutes and Ladders (previously known as Snakes and Ladders in India and the UK). In Chutes and Ladders, some squares on the board tell the player to move forward (go up a ladder) or to move backward (go down a chute). In the "ladders" game, you only move forward.

This article uses Monte Carlo simulation in SAS to show that the "ladders" card trick "works" about 98.2% of the time.

I have been told that Martin Gardner wrote about this game. He referred to mathematical card tricks as those that "do not require prestidigitation," or sleight of hand.

The ladders card trick

The rules of the game and a Python simulation are presented in a blog post by Bob Carpenter, who saw the trick performed at a children's museum. The performer shuffles an ordinary deck of 52 playing cards and places them face up in a row on a table. The performer then describes the game of ladders:

• A player starts by pointing to any card in the first five positions.
• The value of the card indicates the number of cards to move forward. If the card is 2, 3, ..., 9, you move forward that many cards. If the card is a 10, jack, queen, king, or ace, you move forward one space.
• From the new position, apply the rule again. Repeat this process until you cannot advance any more.

The performer selects two volunteers from the audience and tells them each to point randomly to any card from among the first five cards. Each player does so. The performer then announces that both players will end up on a certain "magical" card and he tells everyone the name of the magical card. The players then follow the game rules. Amazingly, each person's path terminates on the magical card that was previously announced. The trick works about 98.2% of the time.

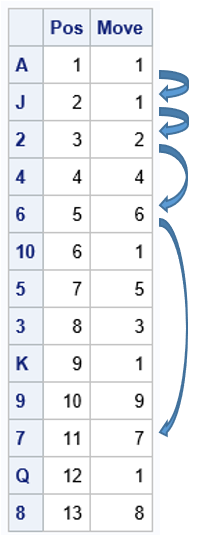
To illustrate the ladders game, first consider a simpler situation of a deck that contains only 13 cards, one for each card value (for example, use only spades). One random shuffle of the 13 cards is shown to the right. For this arrangement of cards, the performer announces that both volunteers will end up on the 7 card (the magical card for this shuffle), which is the 11th card in the row of cards. Suppose the first volunteer points to the ace in the first position as her starting card. The rules of the game dictate the following sequence of moves:

• From the A, the player moves forward one card and lands on the J.
• From the J, the player moves forward one card and lands on the 2.
• From the 2, the player moves forward two cards and lands on the 6.
• From the 6, the player moves forward six cards and lands on the 7. The player cannot move forward seven spaces, so the 7 is her final card, as predicted in advance.

Thus, the path for the first player is the sequence of positions (1, 2, 3, 5, 11).

What happens for the other player? Well, if the second volunteer chooses his initial card at positions 2, 3, or 5, then his path will instantly coincide with the path of the first player, so his path, too, terminates at the 7 card in the 11th position. If the second volunteer chooses his initial card at position 4, then his path hits positions 4, 8, and 11. This path also terminates at the 7 card in the 11th position. Thus, for this set of cards and this shuffle, all initial positions follow a path that eventually lands on the 7.

How does the performer know the name of the final magical card? As he deals, he secretly counts the path determined by the first card in the deck.

Simulate the ladders game in SAS

You can use Monte Carlo simulation to estimate the probability that the ladders card trick "works." To keep it simple, let's say the trick "works" when the paths of the two players converge. That is, the players initially start on two random positions (1-5), but they end up on the same final card after they each follow the path dictated by their initial position. The simulation for the ladders card trick has the following major steps:

1. Set up the card deck. For each card, assign the number of steps to move forward.
2. Create a function that computes the final position, given the initial position and the sequence of moves determined by the shuffled deck.
3. Run the Monte Carlo simulation. This consists of several sub-steps:
   • Shuffle the deck (that is, shuffle the array of moves).
   • Use sampling without replacement to choose two initial positions.
   • Compute the final card for each initial position.
   • Record whether the two paths converged.
4. Estimate the probability of the trick working as the proportion of times that the paths converged in the simulation.

As is often the case, this simulation is easiest to perform in SAS by using the SAS/IML language. You can use the RANPERM function to shuffle the deck. You can use the SAMPLE function to sample without replacement from the values 1-5. You can write a function that computes the final position based on the initial position. The following program is one way to implement a Monte Carlo simulation for the ladders card trick:

/* The Ladders card trick:
   https://statmodeling.stat.columbia.edu/2022/10/07/mira-magic-a-probabilistic-card-trick/
   Lay out a shuffled deck of cards.
   Choose one of the first five cards as a starting point.
   Move down the deck as follows:
   If the current card is 2-9, move that many cards forward.
   For other cards, move one space forward.
*/
proc iml;
/* 1. set up the card deck and assign values. 
   Note: We don't actually need the deck, only the instructions
   about how to move. */
values = {A,'2','3','4','5','6','7','8','9','10', J, Q, K};
advance= {1,  2,  3,  4,  5,  6,  7,  8,  9,  1,  1, 1, 1};
deck  = repeat(values, 4);   /* full deck of 52 cards */
moves = repeat(advance, 4);  /* corresponding moves */
nCards = nrow(moves);
 
/* 2. Find the final position, given the first position and 
   the vector of moves for the current shuffled deck.
   startPos : a scalar value 1-5
   Move : a vector of values. If your current card is in 
          position i, the next card is position (i + Move[i])
*/
start EndPos(startPos, Move);
   Pos = startPos;
   do while(Pos + Move[Pos] < nrow(Move));
      Pos = Pos + Move[Pos];
   end;
   return( Pos );
finish;
 
/* 3. Run the Monte Carlo simulation:
      A. Shuffle the deck (vector of moves)
      B. Use sampling w/o replacement to choose two initial positions
      C. Compute the final card for each initial position
      D. Record whether the two paths converged
*/
call randseed(1234);
NSim = 1E5;
match = j(NSim,1);
do j = 1 to nSim;
   k = ranperm(nCards);          /* shuffle the deck */
   Move = moves[k];
   /* choose two different starting positions in 1-5 */
   startPos = sample(1:5, 2, "NoReplace");
   EndPos1 = EndPos(startPos[1], Move);
   EndPos2 = EndPos(startPos[2], Move);
   match[j] = (EndPos1=EndPos2);
end;
 
/* 4. Estimate probability as the proportion of matches (1s) in a binary vector.
      Optional: Compute a Wald CL for the proportion */
ProbMatch = mean(match);
StdErr = sqrt( ProbMatch*(1-ProbMatch)/ NSim );
CL = ProbMatch + {-1 1}*1.96*StdErr;
print NSim[F=comma9.] ProbMatch StdErr CL[c={'LCL' 'UCL'}];

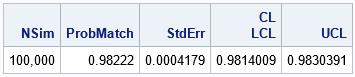
The simulation shows that the two players end up on the same card more than 98% of the time.

Summary

This article describes a probabilistic card trick, which I call the game of ladders. Two players choose random cards as an initial condition, then follow the rules of the game. For about 98.2% of the deals and initial positions, the paths of the two players will converge to the same card. As the performer is laying out the card, he can predict in advance that the paths will converge and, with high probability, announce the name of the final card.

Bob Carpenter's blog post mentions the connection between this card trick and Markov chains. He also presents several variations, such as using more cards in the deck.