A colleague asked how to compute the barycentric coordinates of a point inside a triangle. Given a triangle in the plane with vertices p1, p2, and p3, every point in the triangle can be represented as a convex combination of the vertices: c1*p1 + c2*p2 + c3*p3, where c1,c2,c3 ≥ 0. In addition, the point can be represented uniquely if you require that c1 + c2 + c3 = 1. The triplet (c1, c2, c3) is the barycentric coordinate for the point with respect to the given triangle. You can extend the definition of barycentric coordinates to represent points that are outside of the triangle. For a point outside the triangle, at least one of the barycentric coordinates is negative.

My colleague wanted a solution that would generalize to higher-dimensional tetrahedron and points. I think of barycentric coordinates as a change of basis from the Euclidean coordinate system (the standard coordinate basis vectors) to the basis of the vectors that define a triangle or tetrahedron. In linear algebra, a change of basis is performed by solving a linear system. Because a triangle (tetrahedron) in dimension d is defined by d+1 points, you need to add a linear constraint so that the resulting linear system is nonsingular. By convention, that constraint is that the sum of the barycentric coordinates sum to 1.

This article uses SAS software to compute barycentric coordinates for a triangle or tetrahedron. Because the computation involves vectors and linear transformations, it is easiest to use SAS IML software.

Barycentric coordinates from the perspective of linear algebra

To begin, let's focus on 2-D points and planar triangles. Some explanations of barycentric coordinates use physical terms ("place a weight at each vertex of a triangle..."). Others define the coordinates in terms of areas of subtriangles. Both interpretations are problematic because a point can have a negative barycentric coordinate, but it is hard to imagine a "negative mass" or a "negative area."

Instead, I prefer to think of barycentric coordinates in terms of linear algebra. We are all familiar with Cartesian coordinates, which represent a point in terms of the standard basis vectors. For example, in 3-D, we use the unit basis vectors e1 = (1,0,0), e2 = (0,1,0), and e3 = (0,0,1). When we say that a point has Cartesian coordinates (0.5, 0.7, -0.2), it means that the point is located at 0.5*e1 + 0.7*e2 - 0.2*e3. For unit basis vectors, we can reach the new point by moving 0.5 units along e1, 0.7 units along e2, and 0.2 units in the direction of -e3, which is a vector in the opposite direction of e3.

Barycentric coordinates are similar, but they are defined in terms of three vectors of a reference triangle. You can think of the vertices of a triangle, P, as being defined by three vectors: P1, P2, and P3. A point that has barycentric coordinates (0.5, 0.7, -0.2), it means that the point is located at 0.5*P1 + 0.7*P2 - 0.2*P3. Because we want the barycentric coordinates to be independent of the scaling of the triangle, we standardize the coordinates by insisting that the sum of the coordinates be unity. In our example, 0.5 + 0.7 - 0.2 = 1.

In linear algebra, you learn to change coordinates from one vector basis to another by using a linear transformation. Thus, for each reference triangle, there is a linear transformation (represented by a matrix), that can map any point in Cartesian space into the barycentric coordinates for that triangle. Given a planar point (x,y) and a triangle P that has vertices p1, p2, and p3, you can use the following algorithm to find the barycentric coordinates of with respect to the triangle P:

• Augment the point (x,y) by adding a third coordinate with the value 1. Thus, we consider the vector b=(x,y,1). (Why 1? Because we want the sum of the barycentric coordinates to equal 1.)
• Create a 3-D vector by appending 1 to the vertices of the triangle. Let P1 be the vector corresponding to the vertex p1, and so forth. Construct the 3 x 3 nonsingular matrix whose columns are P1, P2, and P3. Call this matrix A.
• Solve the linear system A*v = b for the vector v. Because of the third row of A and b, the vector v has the property that its elements sum to 1.

The solution, v, is the set of barycentric coordinates for the point (x,y) with respect to the triangle defined by the vertices p1, p2, and p3.

Barycentric coordinates from the perspective of geometry

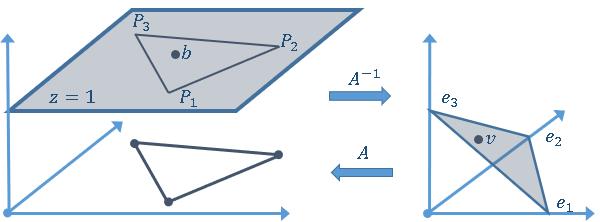
The algorithm in the previous section has a geometric interpretation. Think of the 2-D (x,y) plane as embedded in 3-D Cartesian space. Typically, we think of the plane as being the slice z=0, but you can use any value of z for the embedding. Let's use z=1 instead. Then each point in the (x,y) plane is represented as (x,y,1) in 3-D.

The vertices of the triangle are similarly augmented by using 1 for the third coordinate. Thus, the vertices of a nondegenerate triangle generate a set of linearly independent vectors, P1, P2, and P3. You can use these vectors as a set of basis vectors for 3-D space. In linear algebra, you learn that the matrix A enables you to change coordinates from the basis (e1,e2,e3) to the basis (P1,P2,P3). Geometrically, the matrix A maps the standard simplex in 3-D to the triangle with vertices P1, P2, and P3.

The geometry of the barycentric coordinates is shown in the following diagram. The left image shows the original triangle embedded in 3-D space at the plane z=1. The right image shows the standard simplex, whose vertices are at (1,0,0), (0,1,0), and (0,0,1). (Note that if (c1,c2,c3) is any point on this plane, then c1+c2+c3=1.) The matrix A maps the vertices of the standard simplex to the vertices of the "lifted" triangle. The inverse matrix maps in the other direction.

Thus, the algorithm in the previous section represents a change-of-basis between Cartesian coordinates (on the left) and barycentric coordinates (on the right). From the barycentric coordinates, you can get the original point (augmented by 1) via multiplication by A. For any point in the original (x,y) plane, you can get the barycentric coordinates by "raising up" the point to the plane z=1 and then multiplying by A^-1 or, equivalently, by solving a linear system.

Compute barycentric coordinates in SAS

If you understand the linear algebra behind barycentric coordinates, it is straightforward to write a SAS IML module that computes the barycentric coordinates of a point with respect to a reference triangle:

proc iml;
/* compute barycentric coordinates for x with respect to the triangle 
  whose vertices are the three rows of P. See
  https://en.wikipedia.org/wiki/Barycentric_coordinate_system#Vertex_approach
*/
start Barycentric(x, P);
   A = P` // j(1, nrow(P), 1);       /* add constraint coefficients for sum(barycentric) */
   b = x` // j(1,nrow(x),1);         /* add constraint: sum(barycentric) = 1 */
   v = solve(A, b);
   return( v` );                     /* return a row vector */
finish;
 
/* Define a reference triangle. Each row of P is a vertex. */
P = {0.8 -0.2, 
     0.3  1,
     0    0   };   
 
/* find the barycentric coordinates for a point inside the triangle P */
b = {0.4  0.6};      
c = Barycentric(b, P);
bNames = 'c1':'c3';
print c[L="Barycentric for (0.4, 0.6)" c=bNames];
 
/* verify that b = c1*P[1,] + c2*P[2,] + c3*P[3,] */
v = c*P;             /* we should get back the original point */
print v;

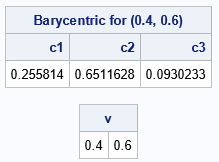
The rows of the matrix P define the vertices of a triangle in the plane. In this example, b is a point in the plane that is inside the triangle. The call to the Barycentric function returns the barycentric coordinates for b. By inspection, you can see that the barycentric coordinates (0.25+0.65+0.1) sum to 1. Furthermore, the computation c*P is shorthand for the linear combination c1*P[1,] + c2*P[2,] + c3*P[3,]. As expected, this combination returns the point b, which shows that barycentric coordinates represent a point as a linear combination of the vertices.

A useful fact about this implementation is that the Barycentric function can compute the barycentric coordinates for multiple points in a single call. The SOLVE function in SAS IML supports solving linear systems for which the right-hand side is a matrix of column vectors. Thus, to compute the barycentric coordinates of multiple points, you can send in a matrix for which each row is a point:

z = { 0.4  0.6,              /* Pt 1: inside triangle */
      0.15 0.5,              /* Pt 2: on edge of triangle */
      0.3  1,                /* Pt 3: on vertex of triangle */
      1    1  };             /* Pt 4: outside triangle */
c = Barycentric(z, P);
print z[c={'x' 'y'} L="Euclidean Coords"], 
      c[c=bNames  L="Barycentric Coords"];

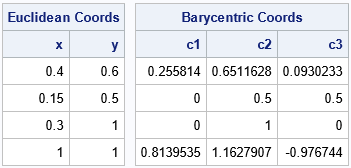
The output shows the barycentric coordinates with respect to the triangle P for four points in the plane. Notice that the barycentric coordinates sum to 1 even if a coordinate is negative.

Barycentric coordinates tell you whether a point is in a triangle

One of the applications of barycentric coordinates is to determine whether a point is inside the reference triangle. Look at the output in the previous section. The following rules are for 2-D triangles. The rules enable you to use the barycentric coordinates to determine whether each input point is inside or outside of the triangle:

• If all barycentric coordinates for a point are positive, then the point is strictly inside the triangle.
• If most barycentric coordinates are positive but one is 0, then the point is on an edge of the triangle.
• If two barycentric coordinates are 0, then the point is a vertex of the triangle.
• If any barycentric coordinate is negative, then the point is outside the triangle.

Recall that you can use a SAS IML subscript reduction operator to compute the maximum value of each row. Thus, the following user-defined function classifies input points are being inside (1) or outside (0) of the reference triangle:

/* For each input point, return 1/0 if the point is inside/outside the triangle
   whose vertices are the rows of P. */
start PtInTriangle(x, P);
   c = Barycentric(x, P);    /* barycentric coordinates */
   return( c[, ><] >=0 );    /* are all coords nonnegative? */
finish;
 
isInside = PtInTriangle(z,P);
print z[c={'x' 'y'}] isInside;

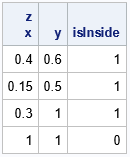
The example uses only four input points, so it is easy to manually verify whether each point is inside or outside of the triangle. The next example generates 1,000 random points, classifies each as being inside or outside of the triangle, and plots the results:

/* generate 1000 points in bounding box of triangle */
call randseed(123);
N = 1000;
x = j(N, 2);
call randgen(x, "uniform", P[><,], P[<>,]);    /* 1000 random uniform points in BBox */
isInside = PtInTriangle(x, P);                 /* for each point, is it in the triangle? */
title "Points Inside and Outside Triangle";
call scatter(x[,1], x[,2]) group=isInside grid={x y};

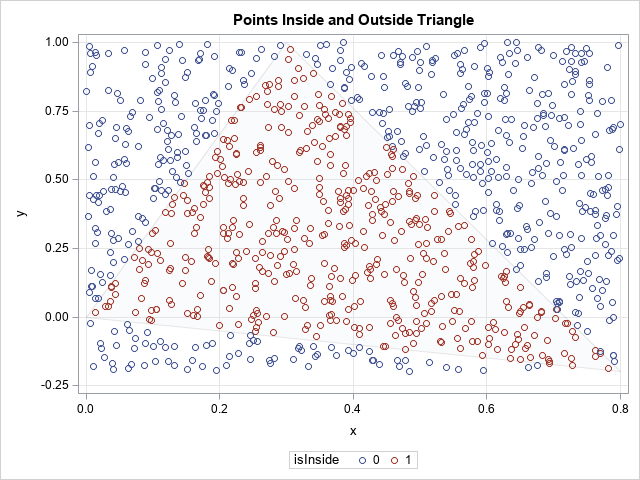
The blue points are outside the triangle, and the red points are inside the triangle. To help you visualize the triangle, I have overlaid the points on a pale gray outline of the triangle.

Generalize the algorithm to tetrahedra

So far, the examples have featured 2-D points and planar triangles. But can you modify the algorithm so that it computes the barycentric coordinates for an n-dimensional tetrahedron?

The answer is yes, but no modifications are needed! As is often the case for linear algebra problems, a matrix formulation works for problems of arbitrary dimensions. For example, the following example defines a 3-D tetrahedron and two 3-D points.

/* generalize to a tetrahedron */
P = {0.8 -0.2 0, 
     0.3  1   0,
     0    0   0,
     0.3  1   1};
 
z = {0.395 0.6  0.2,         /* Pt 1: inside tetrahedron */
     0.36  0.34 0  ,         /* Pt 2: on face of tetrahedron */
     0.15  0.5  0  ,         /* Pt 3: on edge of tetrahedron */
     0.3   1    0  ,         /* Pt 4: on vertex of tetrahedron */
     1     1.04 1  };        /* Pt 5: outside tetrahedron */
c = Barycentric(z, P);
isInside = PtInTriangle(z,P);
 
bNames = 'c1':'c4';
print c[c=bNames  L="Barycentric Coords"],
      IsInside[c='IsInside' L='Classify'];

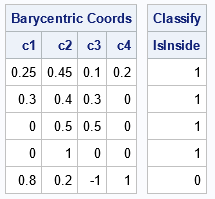
Again, the barycentric coordinates tell you whether the point is inside the tetrahedron. The rules from the previous section generalize so that you can tell whether a point is on a face, edge, or vertex:

• A point is inside the tetrahedron if the barycentric coordinates are all positive.
• A point is outside the tetrahedron if any barycentric coordinate is negative.
• If a point is inside the tetrahedron and a barycentric coordinate is 0, the point is on a face, edge, or vertex. For example, the coordinates of the second point have one zero, so the point is on a face. The coordinates of the third point have two zeros, so the point is on an edge, and so forth.

Summary

This article shows how to use linear algebra and geometry to define barycentric coordinates for a triangle or a tetrahedron. You can compute barycentric coordinates by using a matrix formulation that works for any nondegenerate tetrahedron, regardless of the dimensions of the points. By using the barycentric coordinates, you can determine whether a point is inside or outside of a tetrahedron. You can even identify points that are on faces, edges, or vertices of the reference tetrahedron.