In a previous article, I discussed the Wilcoxon signed rank test, which is a nonparametric test for the location of the median. The Wikipedia article about the signed rank test mentions a variation of the test due to Pratt (1959). Whereas the standard Wilcoxon test excludes values that equal μ₀ (the target value for the null hypothesis), Pratt's modification includes these values when ranking the data. However, it excludes the ranks from the test statistic. Pratt's modification is not available in PROC UNIVARIATE in SAS, but you can implement it by using the SAS IML language.

Although it is easy to implement Pratt's test statistic, computing the p-values is more of a challenge. For the Wilcoxon signed rank test, PROC UNIVARIATE provides exact p-values for small data sets by computing the exact distribution of the statistic under the null hypothesis. It would be nice to also have exact p-value for Pratt's statistic. This can also be programmed in PROC IML, although it is complicated.

Fortunately, Leuchs and Neuhäuser (2010) published a paper that includes a SAS macro that uses SAS IML to compute the signed rank statistic, Pratt's modification, and the exact p-values for each test. This article shows how to download and use Leuchs and Neuhäuser's macro, which is called %SIGNEDRANK.

Downloading the %SIGNEDRANK macro

Leuchs and Neuhäuser published their paper in an open-access journal, so you can download the paper and their macro for free. However, the macro is distributed in a PDF file, which leads to two problems. First, if you copy and paste the text from the PDF, you sometimes get garbled characters in the program. Second, if you copy/paste from the PDF file, the formatting/indenting of the program is not preserved.

To enable more people to use the macro, I copied it into a text file, reformatted it, and fixed all garbled characters. I then uploaded the macro to a GitHub site where it can be accessed by anyone. I copied the "long version of the macro," which is more general and supports one-sided p-values.

In addition to reformatting the code, I made two small changes to the macro:

• I added calls to the UPCASE function (or the %UPCASE macro) so that the macro supports case-insensitive options.
• I added code so that several arguments to the macro are now optional and have default values.
• I use the PVALUE6.4 format for the p-values that the macro displays.

You must download and define the macro before you can use it. The traditional way is to download the %SIGNEDRANK macro to a local directory and use %INCLUDE to define the macro in your current SAS session. Alternatively, SAS supports downloading content directly from GitHub. The following DATA step shows how to download the macro to the WORK libref and use the %INCLUDE statement to define the macro from that location:

/* define GitHub repo (source) and the local directory (destination) */
options dlcreatedir;                       /* create RepoPath directory if it doesn't exist */
%let gitURL = https://github.com/sascommunities/the-do-loop-blog/;  /* Git repo to copy */
%let RepoPath = %sysfunc(getoption(WORK))/BlogRepo;                 /* location to put copy */
 
/* Clone the GitHub repo into RepoPath; if exists, skip download */
data _null_;
if fileexist("&RepoPath.") then do;
   put 'Repository already exists; skipping the clone operation';
end;
else do;
   put "Cloning repository from &gitURL";
   /* NOTE: use GITFN_CLONE for 9.4M5; use GIT_CLONE for 9.4M6 and for Viya */
   rc = git_clone("&gitURL", "&RepoPath." ); 
end;
run;
 
/* read the SAS program that defines the %SIGNEDRANK macro */
%include "&RepoPath/signed-rank/SignedRankMacro.sas";

After running these statements, the %SIGNEDRANK macro is defined in your current SAS session.

Using the %SIGNEDRANK macro

When I try a new computational routine, I always test it on a problem for which I already know the answer. Leuchs and Neuhäuser (2010) use the following data (from Table 1) to demonstrate the macro:

/* data (Table 1) in Leuchs and Neuhäuser (2010) */
data Leucocytes;
input Leucocytes_Before Leucocytes_After @@;
Diff = Leucocytes_Before - Leucocytes_After;
label Leucocytes_Before="Millions of Leucocytes/h (baseline)"
      Leucocytes_After ="Millions of Leucocytes/h (after treatment)"
      Diff = "Difference (Baseline - After)";
datalines;
1.1 0.3   3.4 0.4   2.5 0.2   4.5 0.2   5.1 0.3
7.3 2.8   4.9 4.9   3.3 0.5   2.2 4.2   6.0 6.0
;

Leuchs and Neuhäuser provide the following results for analyzing the differences between pre-treatment and post-treatment leucocyte counts in these 10 patients:

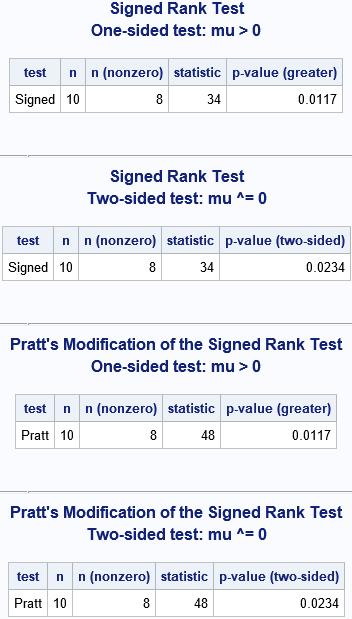
1. For Wilcoxon's signed rank test, the %SIGNEDRANK macro uses the sum of the positive ranks as a test statistic. For these data, the test statistic is 34. The one-sided p-value for the hypothesis "median greater than zero" is 0.0117. The two-side p-value is for the alternative "median different from zero" is 0.0234.
2. For Pratt's modification of the signed rank test, the test statistic is 48. The one-sided p-value is again 0.0117, and the two-side p-value is again 0.0234. Leuchs and Neuhäuser state, "This example yields the same p-values. Note that there are examples where the p-values differ."

Let's run the macro for these four scenarios and make sure we get the same values as Leuchs and Neuhäuser:

title "Signed Rank Test";
title2 "One-sided test: mu > 0";
%signedrank(Leucocytes, Diff, 'Signed', 'Greater');
title2 "Two-sided test: mu ^= 0";
%signedrank(Leucocytes, Diff); /* defaults='Signed' and 'two' */
 
title "Pratt's Modification of the Signed Rank Test";
title2 "One-sided test: mu > 0";
%signedrank(Leucocytes, Diff, 'Pratt', 'Greater');
title2 "Two-sided test: mu ^= 0";
%signedrank(Leucocytes, Diff, 'Pratt'); /* default='two' */

Comparison with PROC UNIVARIATE

I must point out that the test statistic that the %SIGNEDRANK macro uses is different from the test statistic use by PROC UNIVARIATE. However, they are related by a constant value, so the p-values are the same, as explained in a previous article. The macro uses the sum of the positive ranks (T₊) as the test statistic. The test statistic in PROC UNIVARIATE is T₊ – n_t (n_t +1) / 4, where n_t is the number of nonzero observations. This number is reported by the %SIGNEDRANK macro, so you can convert one test statistic into the other. For this example, the test statistic from PROC UNIVARIATE ought to be 34 - 8*(8+1)/4 = 16. Let's run the two-sided signed rank test in PROC UNIVARIATE for comparison:

proc univariate data=Leucocytes mu0=0;
   var Diff;
   ods select TestsForLocation;
run;

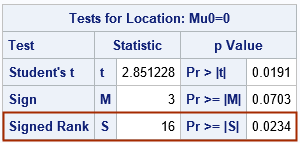
The test statistic is as expected, and the p-value is the same as for the %SIGNEDRANK macro.

Why use the %SIGNEDRANK macro?

If PROC UNIVARIATE implements the Wilcoxon signed rank test, why should you use the %SIGNEDRANK macro? For the following reasons:

• PROC UNIVARIATE computes exact p-values only for n_t ≤ 20. For larger samples, PROC UNIVARIATE uses an asymptotic approximation to the distribution of the test statistic. In contrast, the %SIGNEDRANK macro always computes exact p-values.
• The %SIGNEDRANK macro supports Pratt's modification to the signed rank test. Pratt suggests that the modification is useful when you have multiple observations for which the before-after difference is 0.
• The %SIGNEDRANK macro explicitly supports one-sided tests for μ < μ₀ and μ > μ₀, as well as for the two-sided test μ ≠ μ₀.

Summary

This article discusses the %SIGNEDRANK macro, which was written by Leuchs and Neuhäuser (2010). The macro requires a license to SAS IML software. The article shows how to download the macro from GitHub and shows an example of calling the macro. The %SIGNEDRANK macro computes exact p-values for the Wilcoxon signed rank test. It also performs Pratt's modification of the test and computes exact p-values for the modified test.

You can download the SAS code used in this article.

Reference

Leuchs AK, Neuhäuser M. (2010) "A SAS/IML algorithm for exact nonparametric paired tests." GMS Med Inform Biom Epidemiol. 6(1):Doc04. DOI: 10.3205/mibe000104, URN: urn:nbn:de:0183-mibe0001041 Freely available from: http://www.egms.de/en/journals/mibe/2010-6/mibe000104.shtml

Appendix: Exact p-values for larger problems

A common problem with exact p-values is that the computation is expensive and is only feasible for small samples. Leuchs and Neuhäuser used SAS IML to implement a very efficient algorithm due to Munzel & Brunner (2002). I have run the %SIGNEDRANK macro on a sample with 200 observations, and it ran very quickly. However, be aware that the computational time depends on the number of unique differences in the data.

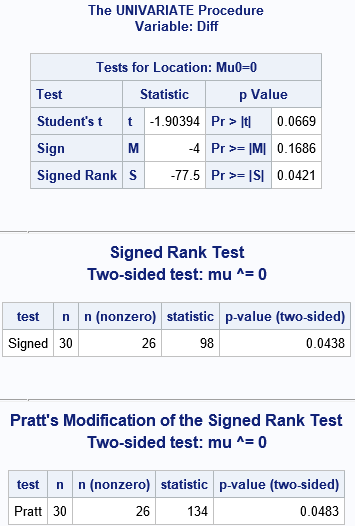
As mentioned earlier, PROC UNIVARIATE uses an asymptotic approximation to compute p-values when the number of nonzero values exceeds 20. The following data set contains 26 nonzero differences. Accordingly, the p-value from PROC UNIVARIATE is approximate whereas the p-value from the macro is exact. Recall also that the test statistics are related by S = T₊ - 26*(26+1)/4, or S = T₊ - 175.5. The following statements also run Pratt's modification on this sample. Notice that Pratt's modification gives a slightly larger p-value for these data as compared to the Wilcoxon test.

/* a larger example: N=30, and nt=26 nonzero differences */
data Test;
input Before After @@;
Diff = Before - After; 
datalines;
12 13   12 13   13 13   11 13  15 13
14 13   13 13   14 14   15 13  16 18
13 15   14 16   17 18   12 14  15 14
14 16   15 17   16 18   14 15  14 17
17 17   12 15   14 16   13 18  18 17
13 15   13 12   14 13   16 12  15 13
;
 
proc univariate data=Test mu0=0;
   var Diff;
   ods select TestsForLocation;
run;
 
title "Signed Rank Test";
title2 "Two-sided test: mu ^= 0";
%signedrank(Test, Diff); /* defaults='Signed' and 'two' */
 
title "Pratt's Modification of the Signed Rank Test";
title2 "Two-sided test: mu ^= 0";
%signedrank(Test, Diff, 'Pratt'); /* default='two' */