The collinearity problem is to determine whether three points in the plane lie along a straight line. You can solve this problem by using middle-school algebra. An algebraic solution requires three steps. First, name the points: p, q, and r. Second, find the parametric equation for the line that passes
Converting a program from one language to another can be a challenge. Even if the languages share many features, there is often syntax that is valid in one language that is not valid in another. Recently, a SAS programmer was converting a program from R to SAS IML. He reached
In several previous articles, I've shown how to use SAS to fit models to data by using maximum likelihood estimation (MLE). However, I have not previously shown how to obtain standard errors for the estimates. This article combines two previous articles to show how to obtain MLE estimates and the
A previous article shows how to use Monte Carlo simulation to approximate the sampling distribution of the sample mean and sample median. When x ~ N(0,1) are normal data, the sample mean is also normal, and there are simple formulas for the expected value and the standard error of the
An elementary course in statistics often includes a discussion of the sampling distribution of a statistic. The canonical example is the sampling distribution of the sample mean. For samples of size n that are drawn from a normally distribution (X ~ N(μ, σ)), the sample mean is normally distributed as
A previous article discusses the birthday problem and its generalizations. The classic birthday problem asks, "In a room that contains N people, what is the probability that two or more people share a birthday?" The probability is much higher than you might think. For example, in a room that contains
The birthday-matching problem (also called the birthday paradox or simply the birthday problem), is a classic problem in probability. Simply stated, the birthday-matching problem asks, "If there are N people in a room, what is the chance that two of them have the same birthday?" The problem is sometimes called
The documentation for Python's SciPy package provides a table that concisely summarizes functions that are associated with continuous probability distributions. This article provides a similar table for SAS functions. For more information on the CDF, PDF, quantile, and random-variate functions, see "Four essential functions for statistical programmers." SAS functions for
Many SAS procedures support a BY statement that enables you to perform an analysis for each unique value of a BY-group variable. The SAS IML language does not support a BY statement, but you can program a loop that iterates over all BY groups. You can emulate BY-group processing by
There are many ways to model a set of raw data by using a continuous probability distribution. It can be challenging, however, to choose the distribution that best models the data. Are the data normal? Lognormal? Is there a theoretical reason to prefer one distribution over another? The SAS has
There are dozens of common probability distributions for a continuous univariate random variable. Familiar examples include the normal, exponential, uniform, gamma, and beta distributions. Where did these distributions come from? Well, some mathematician needed a model for a stochastic process and wrote down the equation for the distribution, typically by
In a previous article, I discussed the Wilcoxon signed rank test, which is a nonparametric test for the location of the median. The Wikipedia article about the signed rank test mentions a variation of the test due to Pratt (1959). Whereas the standard Wilcoxon test excludes values that equal μ0
Wilcoxon's signed rank test is a popular nonparametric alternative to a paired t test. In a paired t test, you analyze measurements for subjects before and after some treatment or intervention. You analyze the difference in the measurements for each subject, and test whether the mean difference is significantly different
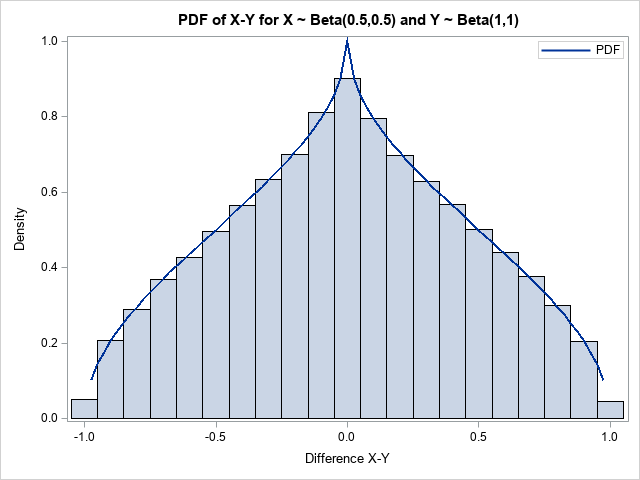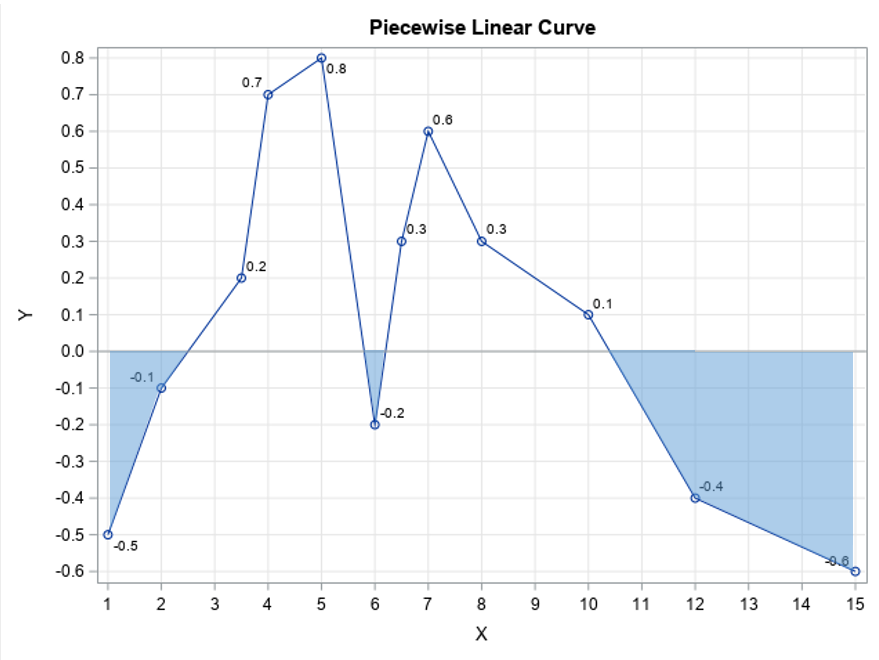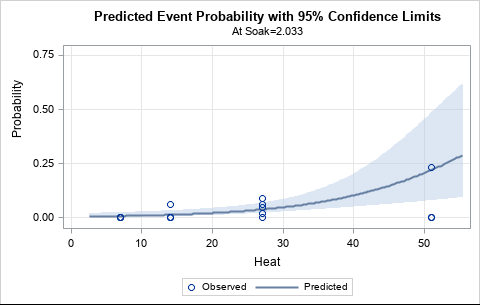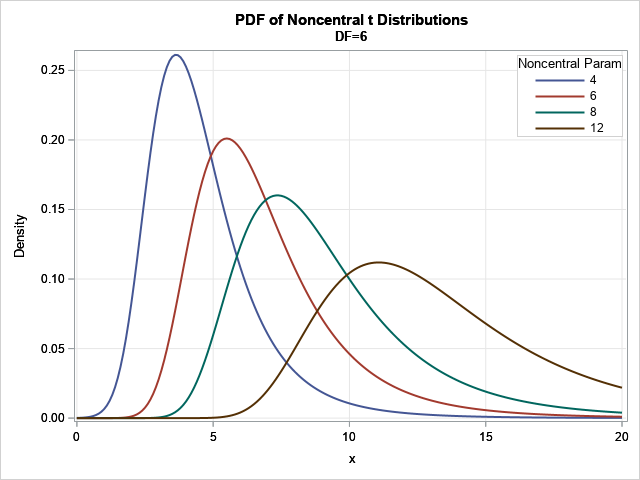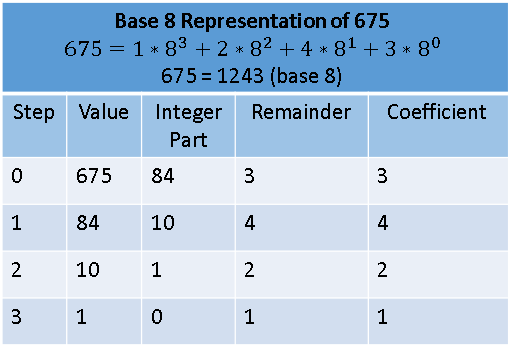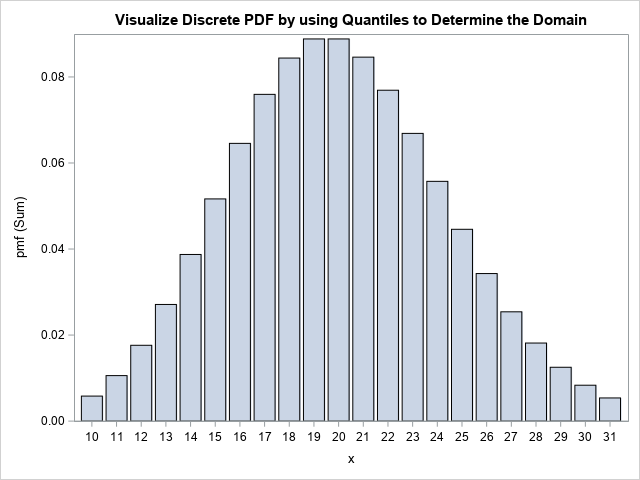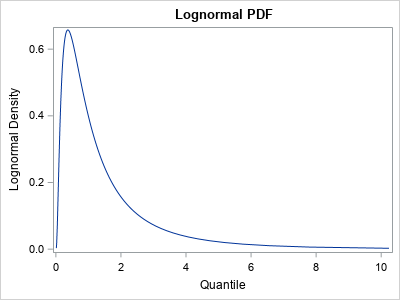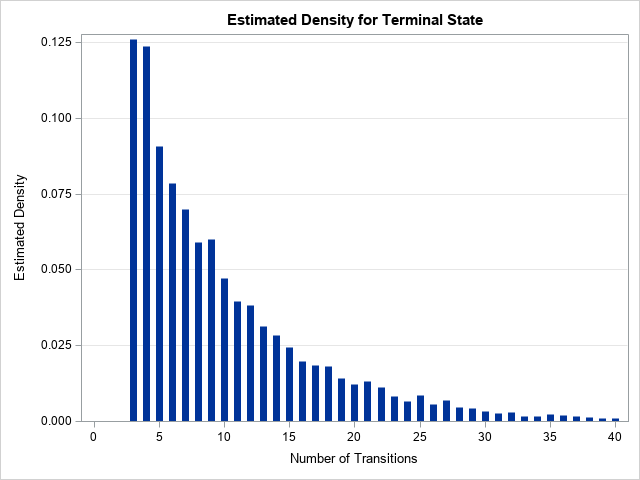
A previous article shows an example of a Markov chain model and computes the probability that the system ends up in a terminal state (called an absorbing state). As explained previously, you can often compute exact probabilities for questions about Markov chains. Nevertheless, it can be useful to know how
A previous article shows how to model the probabilities in a discrete-time Markov chain by using a Markov transition matrix. A Markov chain is a discrete-time stochastic process for which the current state of the system determines the probability of the next state. In this process, the probabilities for transitioning
Given a set of N points in k-dimensional space, can you find the location that minimizes the sum of the distances to the points? The location that minimizes the distances is called the geometric median of the points. For univariate data, the "points" are merely a set of numbers $${p_1,
Labeling objects in graphs can be difficult. SAS has a long history of providing support for labeling markers in scatter plots and for labeling regions on a map. This article discusses how the SGPLOT procedure decides where to put a label for a polygon. It discusses the advantages and disadvantages
SAS supports many ways to compute the rank of a numeric variable and to handle tied values. However, sometimes I need to rank the values in a character categorical variable. For example, the values {"Male", "Female", "Male"} have ranks {2, 1, 2} because, in alphabetical order, "Female" is the first-ranked
A previous article defines the silhouette statistic (Rousseeuw, 1987) and shows how to use it to identify observations in a cluster analysis that are potentially misclassified. The article provides many graphs, including the silhouette plot, which is a bar chart or histogram that displays the distribution of the silhouette statistic
A lot of programmers have been impressed by the ability of ChatGPT, GPT-4, and Bing Chat to write computer programs. Recently, I wrote an article that discusses an elementary programming assignment, called FizzBuzz, which is sometimes used as part of a hiring process to assess a candidate's basic knowledge of
The fundamental operations on sets are union, intersection, and set difference, all of which are supported directly in the SAS IML language. While studying another programming language, I noticed that the language supports an additional operation, namely the symmetric difference between two sets. The language also supports query functions to
I recently discussed introductory programming with a colleague who teaches Python at a university. He told me about the following introductory programming assignment: Let N be an integer parameter in the range [1, 9]. For each value of N, find all pairs of one-digit positive integers d1 and d2 that
In a previous article about Markov transition matrices, I mentioned that you can estimate a Markov transition matrix by using historical data that are collected over a certain length of time. A SAS programmer asked how you can estimate a transition matrix in SAS. The answer is that you can
Most homeowners know that large home improvement projects can take longer than you expect. Whether it's remodeling a kitchen, adding a deck, or landscaping a yard, big projects are expensive and subject to a lot of uncertainty. Factors such as weather, the availability of labor, and the supply of materials,
A previous article describes the metalog distribution (Keelin, 2016). The metalog distribution is a flexible family of distributions that can model a wide range of shapes for data distributions. The metalog system can model bounded, semibounded, and unbounded continuous distributions. This article shows how to use the metalog distribution in
Undergraduate textbooks on probability and statistics typically prove theorems that show how the variance of a sum of random variables is related to the variance of the original variables and the covariance between them. For example, the Wikipedia article on Variance contains an equation for the sum of two random
A SAS programmer wanted to compute the distribution of X-Y, where X and Y are two beta-distributed random variables. Pham-Gia and Turkkan (1993) derive a formula for the PDF of this distribution. Unfortunately, the PDF involves evaluating a two-dimensional generalized hypergeometric function, which is not available in all programming languages.
I previously discussed how to use the PUTLOG statement to write a message from the DATA step to the log in SAS. The PUTLOG statement is commonly used to write notes, warnings, and errors to the log. This article shows how to use the PRINTTOLOG subroutine in SAS IML software
A probabilistic card trick is a trick that succeeds with high probability and does not require any skill from the person performing the trick. I have seen a certain trick mentioned several times on social media. I call it "ladders" or the "ladders game" because it reminds me of the
Recently, I needed to know "how much" of a piecewise linear curve is below the X axis. The coordinates of the curve were given as a set of ordered pairs (x1,y1), (x2,y2), ..., (xn, yn). The question is vague, so the first step is to define the question better. Should
