Convert integers from base 10 to another base

An integer can be represented in many ways. This article shows how to represent a positive integer in any base b. The most common base is b=10, but other popular bases are b=2 (binary numbers), b=8 (octal), and b=16 (hexadecimal). Each base represents integers in different ways. Think of a "representation" as a name that is assigned to each integer. This article shows a mathematical algorithm for representing an integer in base b ≥ 2. It implements the algorithm by using the SAS DATA step.

This process is commonly called "converting" an integer from base 10 to base b, but that is a slight misnomer. An integer has an intrinsic value regardless of the base that you use to represent it. We aren't converting from base 10, although we typically use base 10 to input the number into a computer. I prefer to use the term "represent the integer" when discussing the process of writing it in a specified base.

Represent an integer in any base

The most common way to represent an integer is to use base 10, which represents each positive integer as a sum
$x = \sum\nolimits_{i=0}^p {c_i} 10^i$
where the $c_i$ are integers $0 \leq c_i < 10$ . Notice that this sum of powers looks like a polynomial, so the c_i are often called coefficients. (If you require the leading coefficient to be nonzero, the representation is unique.) For example, the number 675 (base 10) can be represented as 6*10² + 7*10¹ + 5*10⁰. So, the ordered tuple (6,7,5) represents the integer in base 10. We usually concatenate the tuple values and simply write 675 and optionally add "base 10" if the base in unclear.

We call this representation "base 10" because it represents a number as a sum of powers of 10. The phrase "change the base" means that we represent the same number as a sum of powers of some other positive integer. For example, the number 675 (base 10) can be represented as 1243 (base 8) because 675 = 1*8³ + 2*8² + 4*8¹ + 3*8⁰. Consequently, the tuple (1,2,4,3) represents the integer in base 8. Equivalently, the coefficients in base 8 are (1,2,4,3).

An algorithm to represent an integer in any base

There is a simple iterative algorithm to represent a positive integer, x, in any base b ≥ 2. The steps in the algorithm are indexed by an integer i=0, 1, 2, ..., k-1, where k is the smallest integer such that x < b^k.

The algorithm works by rewriting the "sum of powers" by using Horner's method. For example, the sum 1*8³ + 2*8² + 4*8¹ + 3*8⁰ can be rewritten as
((1*8 + 2)*8 + 4)*8 + 3.
In this representation, each nested term is some number times 8 (the base) plus a remainder. For a general base, you can write the Horner sum as
(((c[k-1]+...)*b + c[2])*b + c[1])*b + c[0]

The mathematical algorithm exploits Horner's representation, as follows:

Divide the integer, x, by b. In a computer language, the integer-part of the division is FLOOR(x/b) whereas the remainder is MOD(x,b). Write the remainder as the rightmost value in the base b representation of x.
Repeat this process as long as the integer-part of the division is positive. At each step, write the remainder to the left of the previous remainders. When the integer part becomes 0, the process terminates.

For example, let's represent the number 675 (base 10) in base 8. Use x=675 and b=8 as the values in the formulas. The algorithm is as follows:

For i=0: Divide the number 675 by the base, which is 8. You get 84 with 3 as the remainder. So c[0]=3. The number 84 is used in the next step.
For i=1: Divide the number 84 by 8. You get 10 with 4 as the remainder. So c[1]=4.
For i=2: Divide the number 10 by 8. You get 1 with 2 as the remainder. So c[2]=2.
For i=3: Divide the number 1 by 8. You get 0 with 1 as the remainder. So c[3]=1.
Because the integer-part of the previous division is 0, the algorithm terminates.

This process is summarized in the following table for base 8 and the base-10 integer 675:

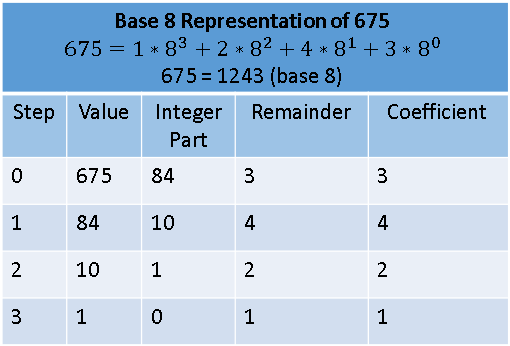
From the coefficients, you can build a string (such as '1243') that represents the number in the given base. For b ≤ 10, the symbols 0, 1, ..., b-1 are used to represent the coefficients. For 10 < b ≤ 36, the letters of the English alphabet represent the higher coefficients: A=10, B=11, C=12, ..., Z=35. The SAS program in the next section uses these symbols to represent the coefficients.

A SAS program for representing an integer in an arbitrary base

Let's put a set of base-10 numbers into a data set:

/* Example data: Base 10 integers to convert to other bases */
data Base10;
input x @@;      /* x >= 0 */
datalines;
2 3 4 5 8 15 31 32 33 49 63 675
;

Because we want to store the representation in a character variable, we set the length of the variable by using the parameter MAXCOEF=32. A string of length 32 is usually sufficient for representing a wide range of integers. The VALUELIST macro defines the set of characters to use to represent each integer as a string for bases b=2, 3, ..., 36. If you want to use a larger base, extend this set of values.

%let maxCoef = 32;    /* how many characters in a string that represents the number? */
%let valueList = ('0' '1' '2' '3' '4' '5' '6' '7' '8' '9' 
                  'A' 'B' 'C' 'D' 'E' 'F' 'G' 'H' 'I' 'J' 'K' 'L' 'M' 
                  'N' 'O' 'P' 'Q' 'R' 'S' 'T' 'U' 'V' 'W' 'X' 'Y' 'Z');

The following SAS DATA step implements the previous algorithm to represent the numbers in a new base. Let's begin by representing the numbers in binary (base 2).

%let base = 2;        /* positive integer. Usually 2 <= base <= 36 */
 
data NewBase;
array values[36] $ _temporary_ &valueList;     /* characters to use to encode values */
array c[0:%eval(&maxCoef-1)]  _temporary_ ;    /* integer coefficients c[0], c[1], ... */
length s $&maxCoef;                            /* string for base b */
b = &base;                                     /* base for representation */
 
set Base10;                                    /* x is a positive integer; represent in base b */
/* compute the coefficients that represent x in Base b */
y = x;
do k = 0 to &maxCoef while(y>0);
   c[k] = mod(y, b);                           /* remainder when r is divided by b */
   y = floor(y / b);                           /* whole part of division */
   substr(s,&maxCoef-k,1) = values[c[k]+1];    /* represent coefficients as string */
end;
keep s x k b;
run;
 
proc print data=NewBase noobs label;
   label x="Base 10" s="Base &base";
   var x s k;
run;

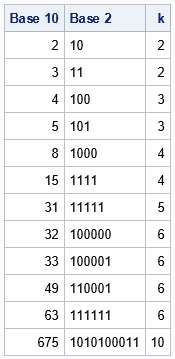
For each positive integer, x, the variable k specifies how many characters are required to represent the number in base 2. (This assumes that you do not want to use leading zeros in the representation.) For example, 31 (base 10) = 11111 (base 2) requires five characters, whereas 32 (base 10) = 100000 (base 2) requires six characters. The program set MAXCOEF = 32, which means that this program can compute the binary representation of any number up to 2³² – 1 = 4,294,967,295 (base 10).

Convert base 10 to octal or hexadecimal

To represent a positive integer in a different base, simply redefine the BASE macro variable and rerun the program. For example, the following statements enable you to convert the numbers to base 8:

%let base = 8;        /* positive integer 2 <= base <= 36 */

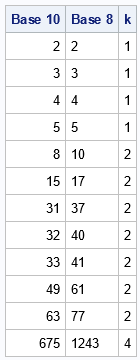
The last row of the table shows that 675 (base 10) = 1243 (base 8), as was shown previously.

For hexadecimal (base 16), you can use the letters 'A' through 'F' to represent the larger values of the coefficients:

%let base = 16;        /* positive integer 2 <= base <= 36 */

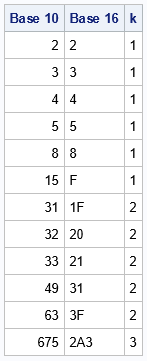
The hexadecimal numbers might be familiar to statistical programmers who use hexadecimal values for RGB colors in statistical graphics. In many programming languages, you can specify a color as a hexadecimal value such as 0x1F313F. The first two digits ('1F') specify the amount of red in the color, the next two digits ('31') specify the amount of green, and the last two digits specify the amount of blue. As an integer, this number is 2044,223 (base 10). You might have seen an advertisement for a computer monitor that claims that the monitor "displays more than 16 million colors." That number is used because FFFFFF (base 16) = 16,777,215 (base 10). In other words, if each red, green, and blue pixel can display 256 colors, the total number of colors is more than 16 million.

Summary

This article shows an algorithm that enables you to represent a positive integer in any base. This is commonly called "converting from base 10," although that is a misnomer. At each step of the algorithm, you use division by the base to find the integer part and remainder of an integer. This algorithm is demonstrated by using the SAS DATA step. As written, the program supports bases 2–36.

Blogs