Rank character variables in SAS

SAS supports many ways to compute the rank of a numeric variable and to handle tied values. However, sometimes I need to rank the values in a character categorical variable. For example, the values {"Male", "Female", "Male"} have ranks {2, 1, 2} because, in alphabetical order, "Female" is the first-ranked element and "Male" is the second-ranked element. Obtaining ranks can be useful in several applications, including graphing. Ranking is a way to obtain a numeric vector (the ranks) from a vector of strings in a way that preserves the relative ordering.

There are several ways to deal with tied values when ranking, but this article uses the "dense" method to assign ranks to tied values. The "dense" method is explained in the documentation of PROC RANK in Base SAS. In the dense ranking, the ranks are integers in the range 1–k, where k is the number of distinct categories.

In SAS, PROC RANK can produce ranks for numeric variables, but not for character variables. There are several ways that I can think of to generate ranks for character variables (see the Appendix), but the method in this article uses the design matrix for the character variable. This article shows a short (two-line) SAS IML function that you can use to generate a vector of integers that represent the alphabetical order (ranks) of the character values.

Statement of the problem

Here is the problem we want to solve. Suppose a character vector, C, has k distinct values. We want to identify the alphabetical rank of each element and use the TIES=DENSE method to break ties. The result is a vector of integers, v, such that 1 ≤ v[i]≤ k and such that C[i]is the v[i]th ranked value of C in alphabetical order.

An example will make things clearer. Suppose C contains the English letters
C = {'C','B','B','A','A','A','C'}.
There are k=3 unique values. If sorted, the first sorted value is 'A', so all 'A' elements are assigned the rank 1. The second ranked value is 'B', so all 'B' elements are assigned the rank 2. Finally, the 'C' elements are assigned the rank 3. The final ranks are
v = {3, 2, 2, 1, 1, 1, 3}.

Rank character values

The documentation for the RANKTIE function in SAS IML software includes a function (RANKTIEC) that can compute the (tied) ranks of a character vector. That function breaks ties by using the TIES=MEAN method. You could modify that function to support the TIES=DENSE method, but I decided to use a different approach. Recall that the design matrix of a character vector (when using a GLM parameterization) is an n x k matrix, D, which has the property that D[i,j]=1 if and only if the (tied) rank of C[i]is j. In other words, the first column in the design matrix is a binary indicator variable that indicates which elements of C are ranked first. The second column indicates which elements are ranked second, and so forth. Thus, the design matrix contains exactly the information you need to solve this problem! You could use IF-THEN-ELSE statements to extract the information from the design matrix, but matrix multiplication is more efficient. You can obtain the ranks by multiplying the vector b={1,2,3,..,k} by D. That is, the ranks are given by v = D*b.

Let's see how this works for a small example. First, let's look at the design matrix, which you can compute by using the DESIGN function in PROC IML:

proc iml;
/* convert letters A-B-C to ranks 1-2-3 */
C = {C,B,B,A,A,A,C};
D = design(C);
print D[rowname=C colname=('col1':'col3')];

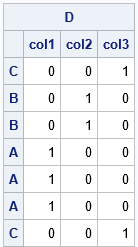
The output shows that the first column of the design matrix identifies the first-ranked elements of C. In general, the i_th column identifies elements that are ranked i_th. You can use this idea to create a function that ranks character values and breaks ties by using the TIES=DENSE method:

start Ranktiec_Dense(C);
   D = design(C); /* an n x k matrix, where k = ncol(unique(C)) */
   rank = D * T(1:ncol(D));
   return rank;   
finish;
 
rank = Ranktiec_Dense(C);
print C rank;

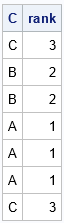
As promised, the vector v provides the tied ranks for the character values in C.

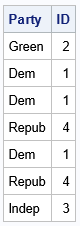
Let's run another small example. The following vector indicates the political parties for seven people. Alphabetically, "Dem" is the first value, and "Repub" is the fourth value. By calling the Ranktiec_Dense function, you obtain a vector that contains the ranks of the character values:

Party = {"Green", "Dem", "Dem", "Repub", "Dem", "Repub", "Indep"};
ID = Ranktiec_Dense(Party);
print Party ID;

Disadvantages of using the design matrix

The design matrix has k columns, where k is the number of unique values in the character vector. Thus, the design matrix is reasonably efficient when there are a small number of unique values, say 100 or less. If you have thousands of unique values, then the design matrix will require a lot of memory to store. In that case, you might want to use a different method. A few ideas are given in the Appendix.

Summary

This article shows how to rank a character vector by using the SAS IML language. The documentation for the RANKTIE function includes a function for ranking where ties are broken by using the TIES=MEAN method. This article provides a function for ranking character values where ties are broken by using the TIES=DENSE method. This method creates a new variable that contains the integers 1–k, where k is the number of unique character values. The alphabetical order of the character variable and the numeric order of the new variable are the same.

Appendix: Other ways to solve this problem

If you need to solve this problem but do not have access to PROC IML, you can solve this problem by using other methods. Some ideas are below. I leave the implementation as an exercise.

Sort the data by the character variable, then use a DATA step and a BY statement to assign ranks to the sorted values. Then "unsort" the data to restore the original order of the observations. This is probably the most natural implementation in SAS.
Use PROC FREQ to enumerate the unique categories. Assign ranks to the categories. Merge the ranks into the original data.
To reproduce the method in this article, use PROC GLMMOD to generate the design matrix and use PROC SCORE to perform the matrix multiplication.

Blogs