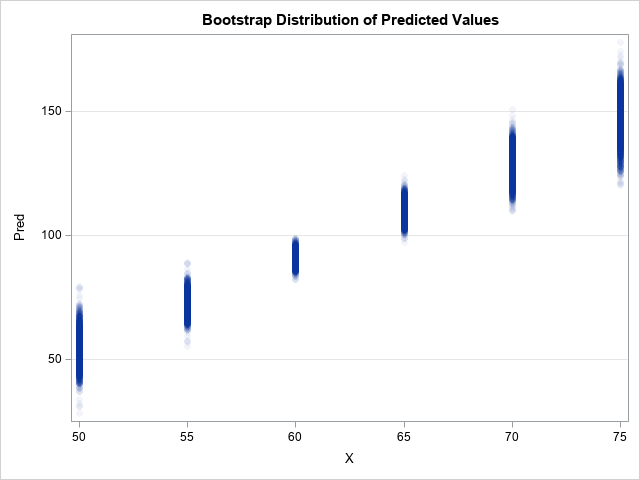
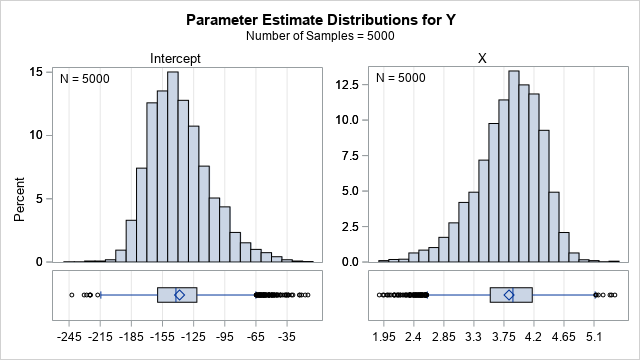
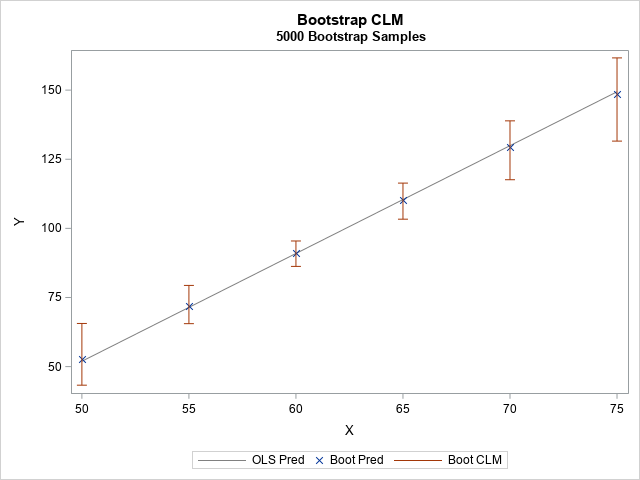
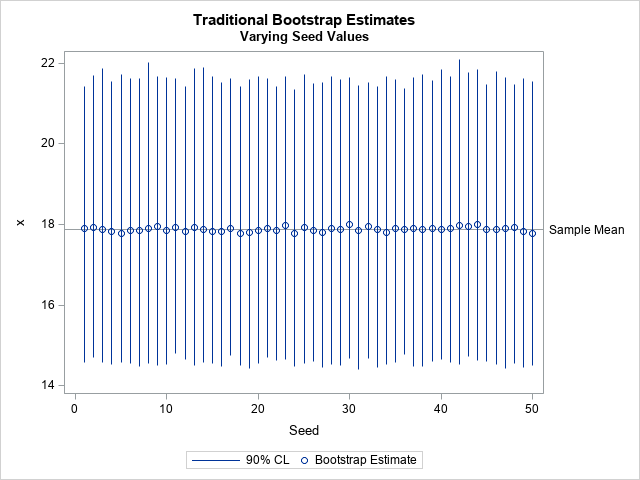
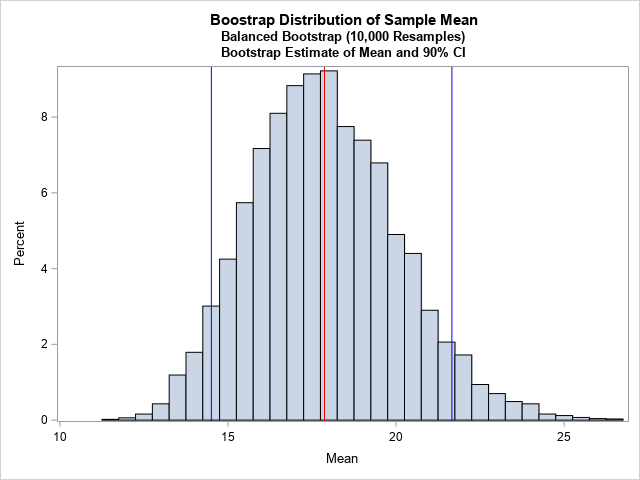
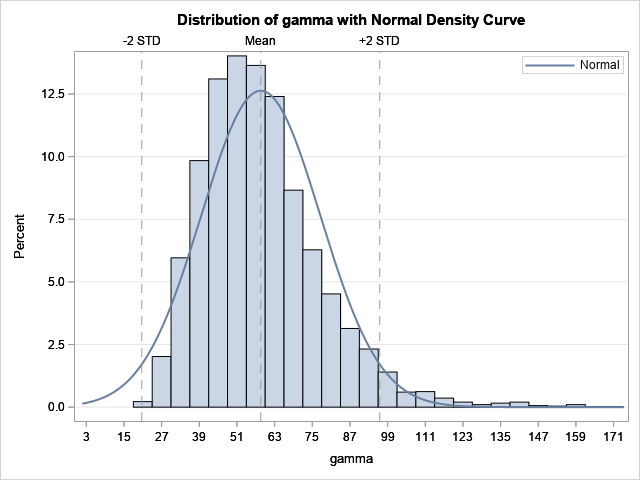
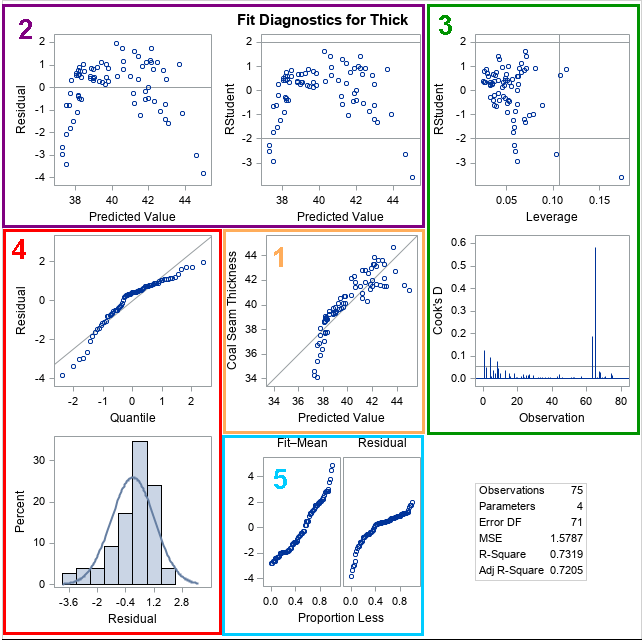
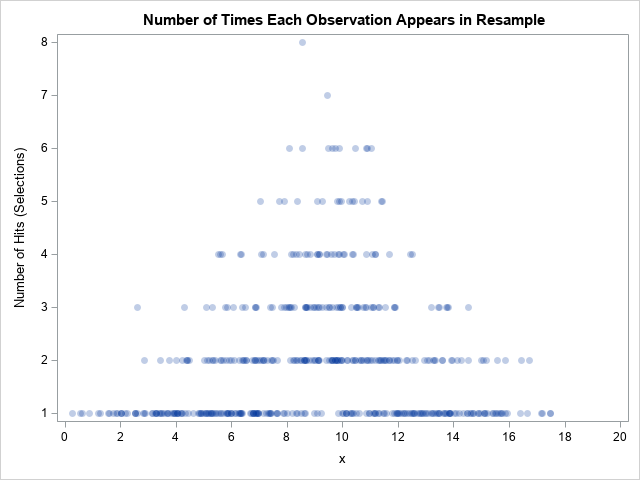
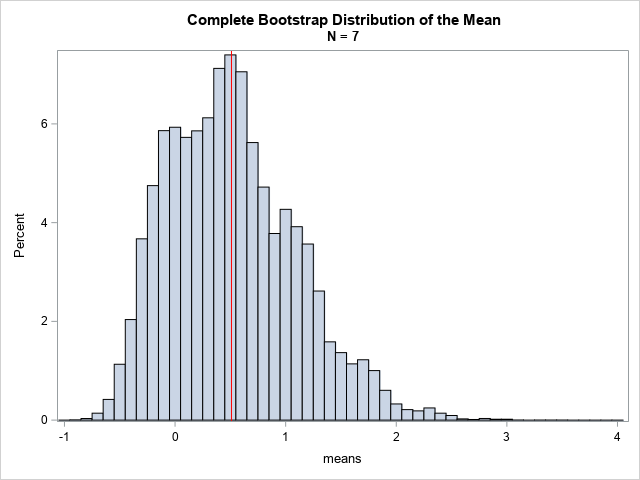
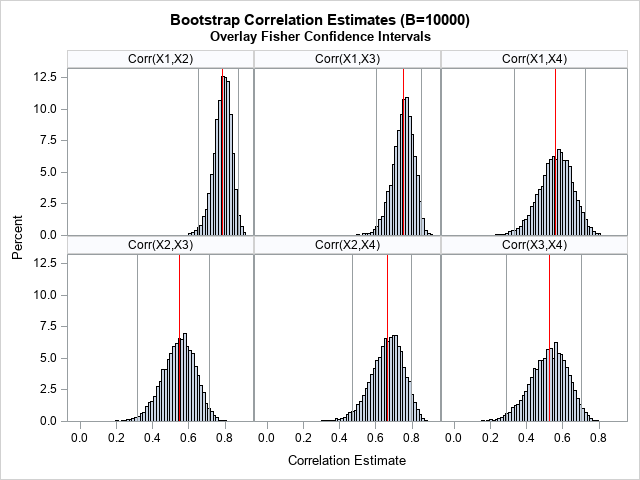
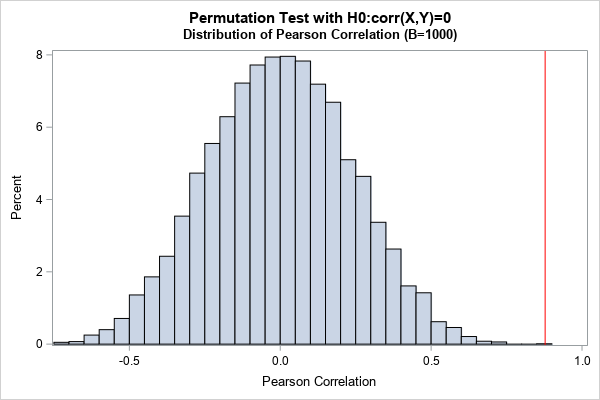
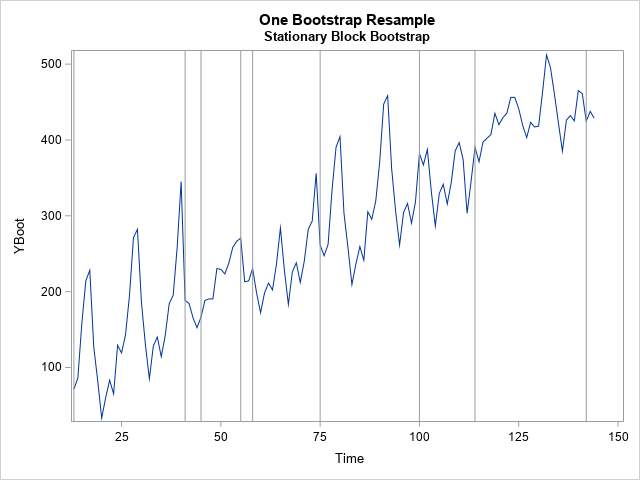
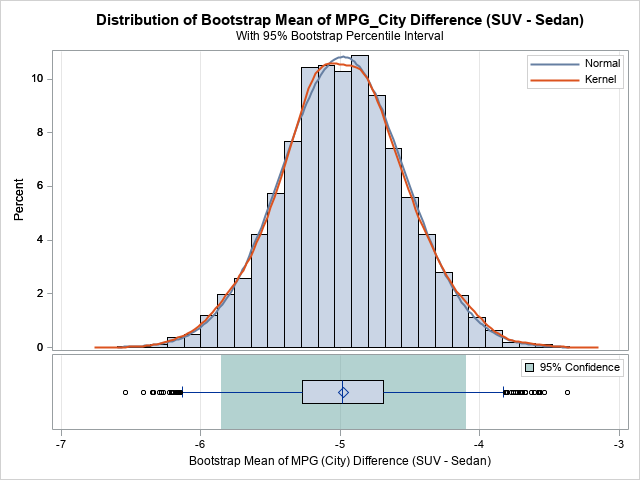
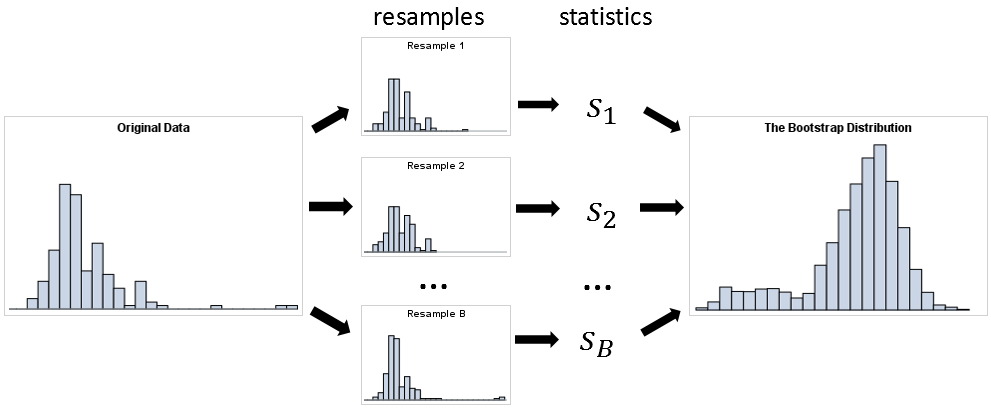
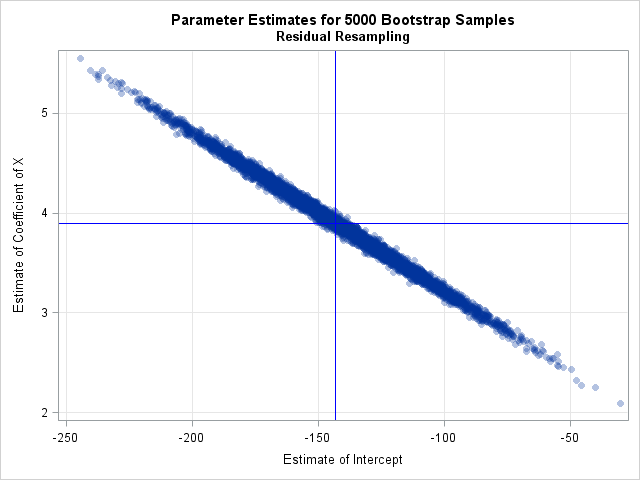
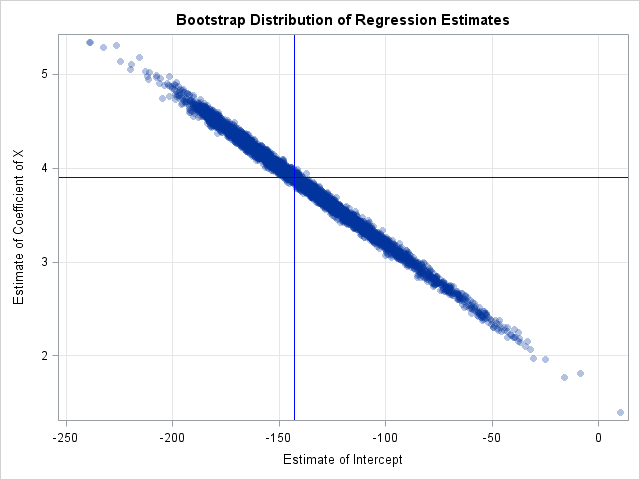
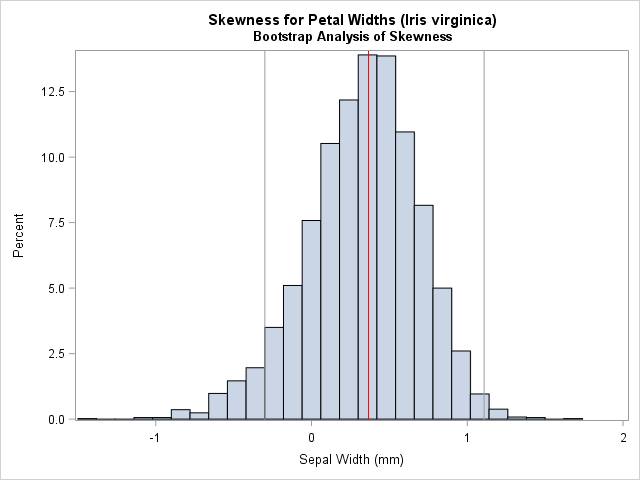
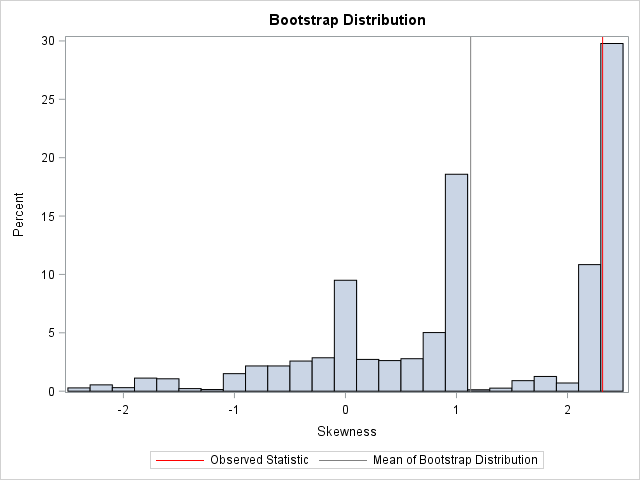
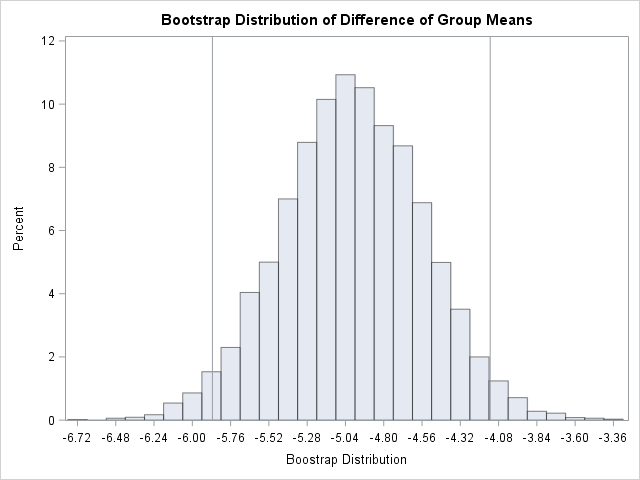
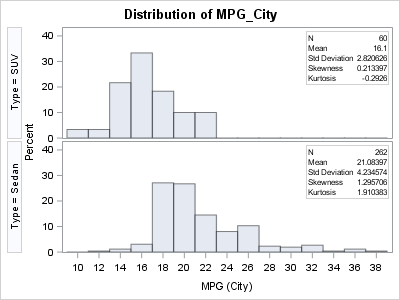
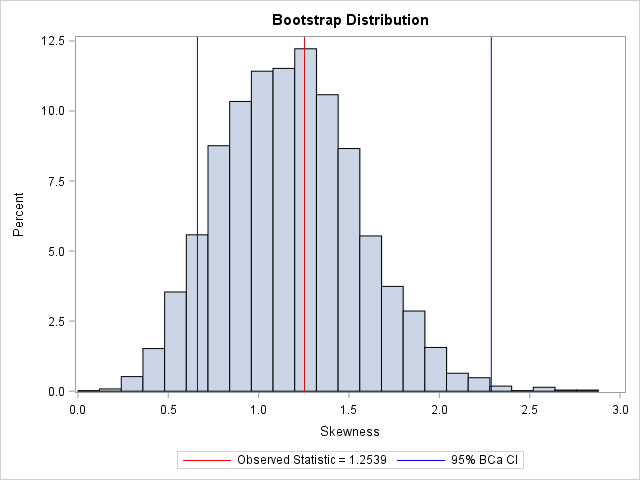
A previous article discusses a formula for a confidence interval for R-square in a linear regression model (Olkin and Finn (1995) "Correlations redux", Psychological Bulletin) The formula is useful for large data sets, but should be used with caution for small samples. At the end of the previous article, I
A previous article shows how to use the MODELAVERAGE statement in PROC GLMSELECT in SAS to perform a basic bootstrap analysis of the regression coefficients and fit statistics. A colleague asked whether PROC GLMSELECT can construct bootstrap confidence intervals for the predicted mean in a regression model, as described in
I've written many articles about bootstrapping in SAS, including several about bootstrapping in regression models. Many of the articles use a very general bootstrap method that can bootstrap almost any statistic that SAS can compute. The method uses PROC SURVEYSELECT to generate B bootstrap samples from the data, uses the
In ordinary least squares regression, there is an explicit formula for the confidence limit of the predicted mean. That is, for any observed value of the explanatory variables, you can create a 95% confidence interval (CI) for the predicted response. This formula assumes that the model is correctly specified and
Many modern statistical techniques incorporate randomness: simulation, bootstrapping, random forests, and so forth. To use the technique, you need to specify a seed value, which determines pseudorandom numbers that are used in the algorithm. Consequently, the seed value also determines the results of the algorithm. In theory, if you know
I have previously blogged about ways to perform balanced bootstrap resampling in SAS. I recently learned about an easier way: Since SAS/STAT 14.2 (SAS 9.4M4), the SURVEYSELECT procedure has supported balanced bootstrap sampling. This article reviews balanced bootstrap sampling and shows how to use the METHOD=BALBOOT option in PROC SURVEYSELECT
In The Essential Guide to Bootstrapping in SAS, I note that there are many SAS procedures that support bootstrap estimates without requiring the analyst to write a program. I have previously written about using bootstrap options in the TTEST procedure. This article discusses the NLIN procedure, which can fit nonlinear
Last year, I wrote almost 100 posts for The DO Loop blog. My most popular articles were about data visualization, statistics and data analysis, and simulation and bootstrapping. If you missed any of these gems when they were first published, here are some of the most popular articles from 2021:
A reader asked whether it is possible to find a bootstrap sample that has some desirable properties. I am using the term "bootstrap sample" to refer to the result of randomly resampling with replacement from a data set. Specifically, he wanted to find a bootstrap sample that has a specific
The number of possible bootstrap samples for a sample of size N is big. Really big. Recall that the bootstrap method is a powerful way to analyze the variation in a statistic. To implement the standard bootstrap method, you generate B random bootstrap samples. A bootstrap sample is a sample
You can use the bootstrap method to estimate confidence intervals. Unlike formulas, which assume that the data are drawn from a specified distribution (usually the normal distribution), the bootstrap method does not assume a distribution for the data. There are many articles about how to use SAS to bootstrap statistics
For many univariate statistics (mean, median, standard deviation, etc.), the order of the data is unimportant. If you sort univariate data, the mean and standard deviation do not change. However, you cannot sort an individual variable (independently) if you want to preserve its relationship with other variables. This statement is
This is the third and last introductory article about how to bootstrap time series in SAS. In the first article, I presented the simple block bootstrap and discussed why bootstrapping a time series is more complicated than for regression models that assume independent errors. Briefly, when you perform residual resampling
As I discussed in a previous article, the simple block bootstrap is a way to perform a bootstrap analysis on a time series. The first step is to decompose the series into additive components: Y = Predicted + Residuals. You then choose a block length (L) that divides the total
For ordinary least squares (OLS) regression, you can use a basic bootstrap of the residuals (called residual resampling) to perform a bootstrap analysis of the parameter estimates. This is possible because an assumption of OLS regression is that the residuals are independent. Therefore, you can reshuffle the residuals to get
A fundamental principle of data analysis is that a statistic is an estimate of a parameter for the population. A statistic is calculated from a random sample. This leads to uncertainty in the estimate: a different random sample would have produced a different statistic. To quantify the uncertainty, SAS procedures
I recently read an article that describes ways to compute confidence intervals for the difference in a percentile between two groups. In Eaton, Moore, and MacKenzie (2019), the authors describe a problem in hydrology. The data are the sizes of pebbles (grains) in rivers at two different sites. The authors
At SAS Global Forum 2019, Daymond Ling presented an interesting discussion of binary classifiers in the financial industry. The discussion is motivated by a practical question: If you deploy a predictive model, how can you assess whether the model is no longer working well and needs to be replaced? Daymond
Many SAS procedures support the BY statement, which enables you to perform an analysis for subgroups of the data set. Although the SAS/IML language does not have a built-in "BY statement," there are various techniques that enable you to perform a BY-group analysis. The two I use most often are
When I run a bootstrap analysis, I create graphs to visualize the distribution of the bootstrap statistics. For example, in my article about how to bootstrap the difference of means in a two-sample t test, I included a histogram of the bootstrap distribution and added reference lines to indicate a
This article describes best practices and techniques that every data analyst should know before bootstrapping in SAS. The bootstrap method is a powerful statistical technique, but it can be a challenge to implement it efficiently. An inefficient bootstrap program can take hours to run, whereas a well-written program can give
If you want to bootstrap the parameters in a statistical regression model, you have two primary choices. The first, case resampling, is discussed in a previous article. This article describes the second choice, which is resampling residuals (also called model-based resampling). This article shows how to implement residual resampling in
If you want to bootstrap the parameters in a statistical regression model, you have two primary choices. The first is case resampling, which is also called resampling observations or resampling pairs. In case resampling, you create the bootstrap sample by randomly selecting observations (with replacement) from the original data. The
Since the late 1990s, SAS has supplied macros for basic bootstrap and jackknife analyses. This article provides an example that shows how to use the %BOOT and %BOOTCI macros. The %BOOT macro generates a bootstrap distribution and computes basic statistics about the bootstrap distribution, including estimates of bias, standard error,
This article shows how to implement balanced bootstrap sampling in SAS. The basic bootstrap samples with replacement from the original data (N observations) to obtain B new samples. This is called "uniform" resampling because each observation has a uniform probability of 1/N of being selected at each step of the
A previous article provides an example of using the BOOTSTRAP statement in PROC TTEST to compute bootstrap estimates of statistics in a two-sample t test. The BOOTSTRAP statement is new in SAS/STAT 14.3 (SAS 9.4M5). However, you can perform the same bootstrap analysis in earlier releases of SAS by using
Bootstrap resampling is a powerful way to estimate the standard error for a statistic without making any parametric assumptions about its sampling distribution. The bootstrap method is often implemented by using a sequence of calls to resample from the data, compute a statistic on each sample, and analyze the bootstrap
The SURVEYSELECT procedure in SAS 9.4M5 supports the OUTRANDOM option, which causes the selected items in a simple random sample to be randomly permuted after they are selected. This article describes several statistical tasks that benefit from this option, including simulating card games, randomly permuting observations in a DATA step,
I wrote more than 100 posts for The DO Loop blog in 2017. The most popular articles were about SAS programming tips, statistical data analysis, and simulation and bootstrap methods. Here are the most popular articles from 2017 in each category. General SAS programming techniques INTCK and INTNX: Do you
I recently showed how to compute a bootstrap percentile confidence interval in SAS. The percentile interval is a simple "first-order" interval that is formed from quantiles of the bootstrap distribution. However, it has two limitations. First, it does not use the estimate for the original data; it is based only
