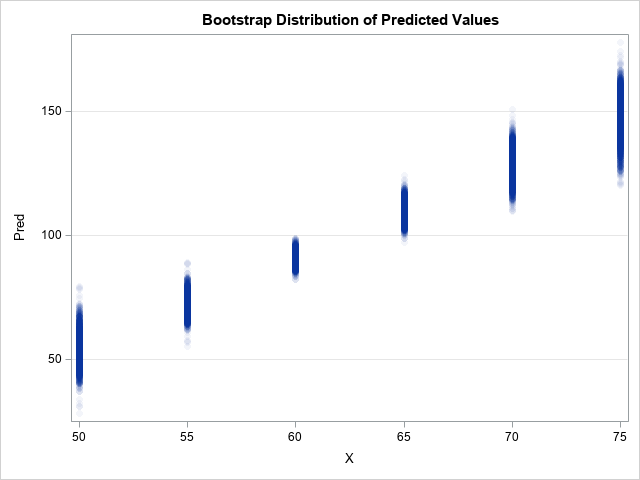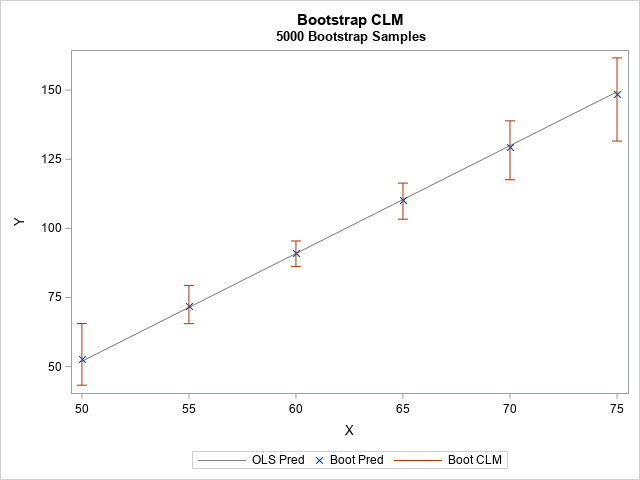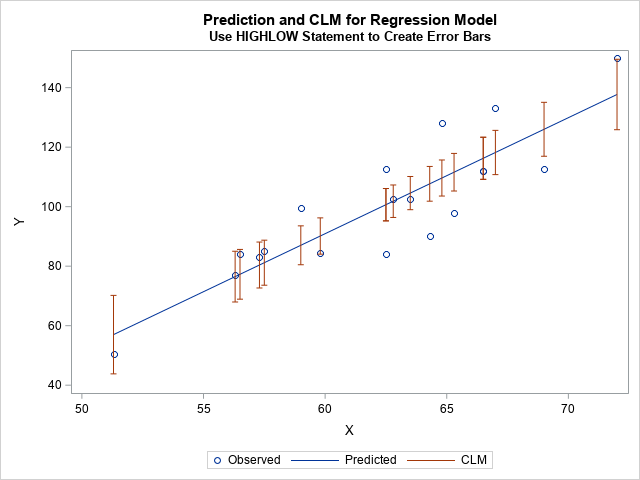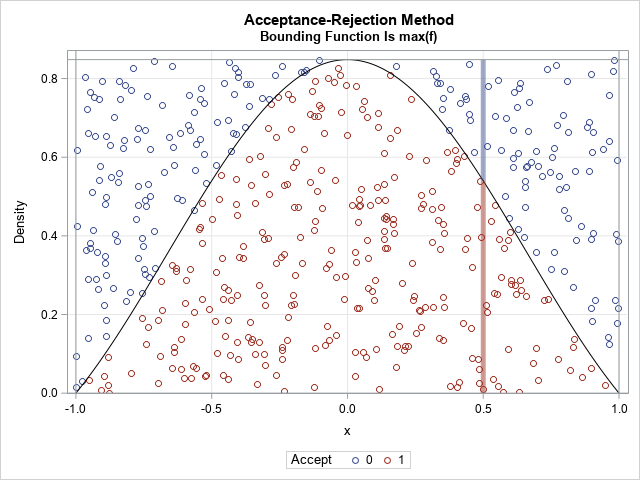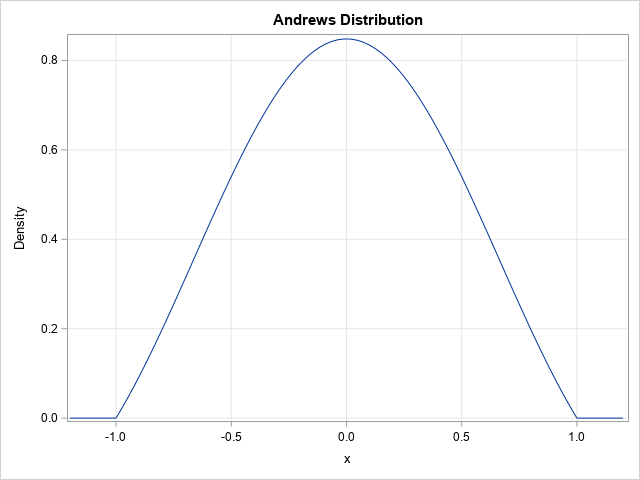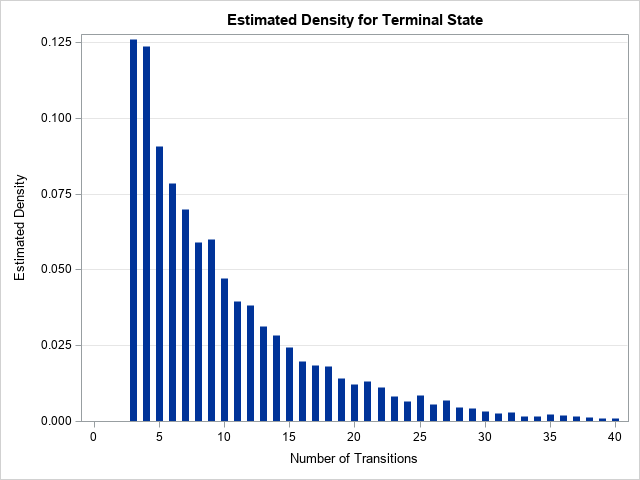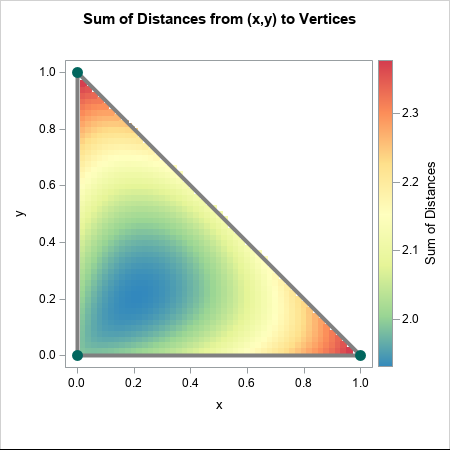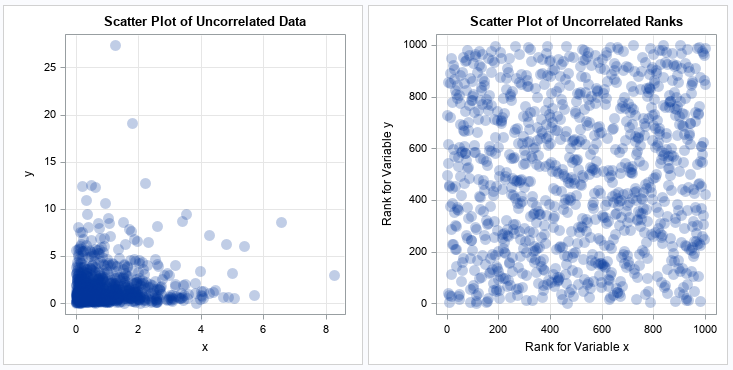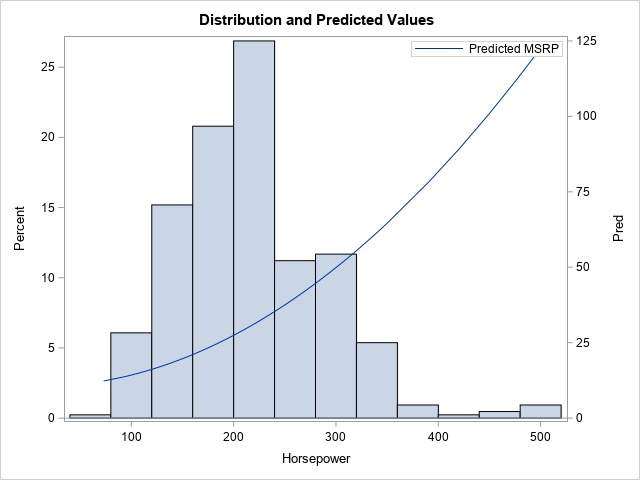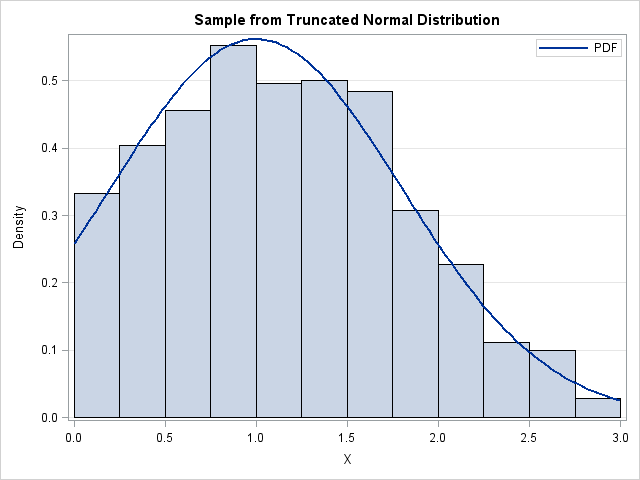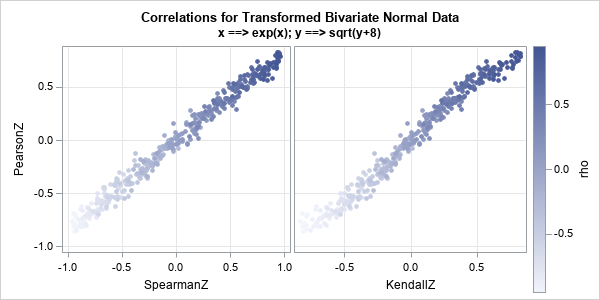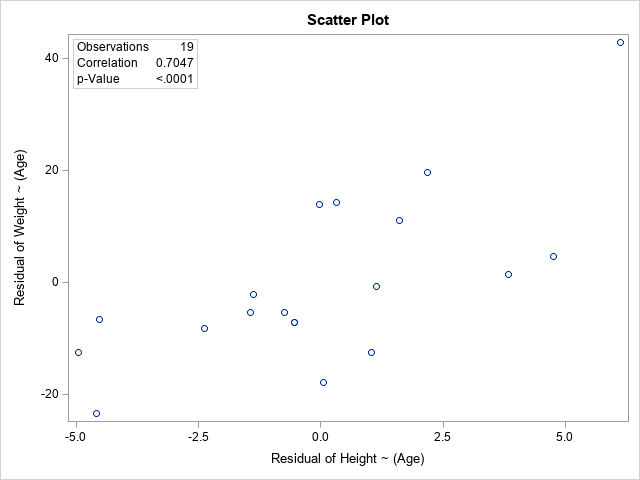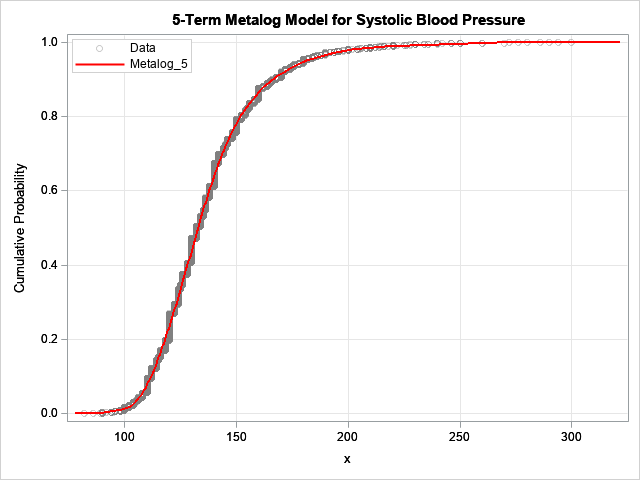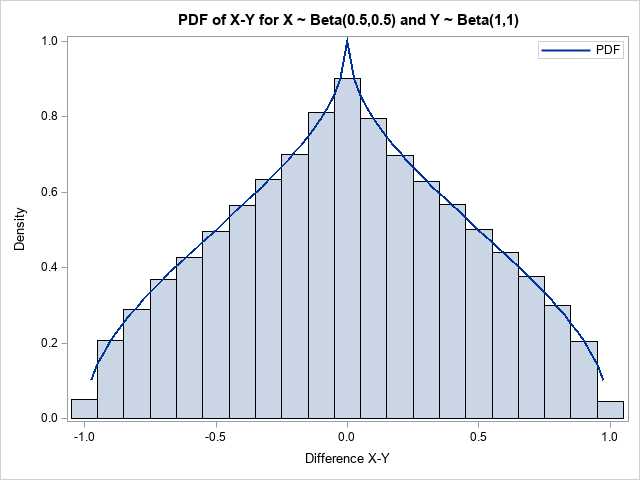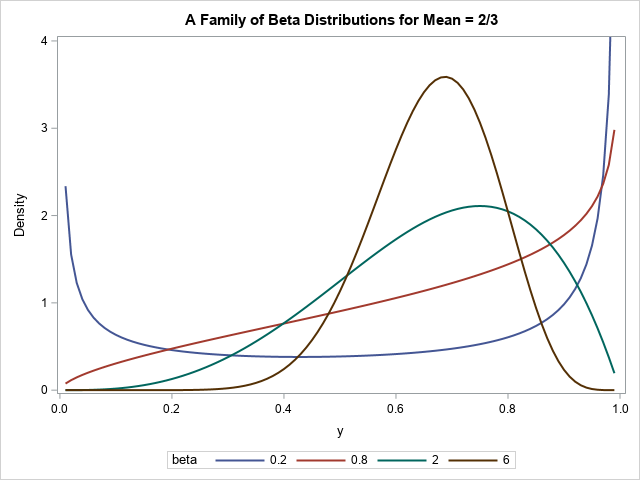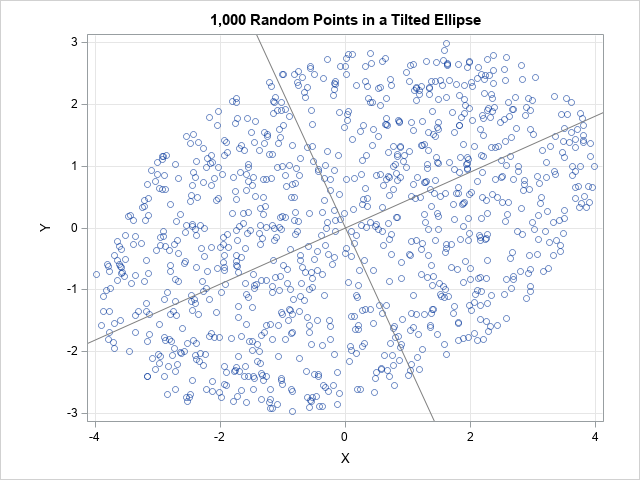
I have previously written about how to efficiently generate points uniformly at random inside a sphere (often called a ball by mathematicians). The method uses a mathematical fact from multivariate statistics: If X is drawn from the uncorrelated multivariate normal distribution in dimensiond, then S = r*X / ||X|| has
A previous article shows how to use the MODELAVERAGE statement in PROC GLMSELECT in SAS to perform a basic bootstrap analysis of the regression coefficients and fit statistics. A colleague asked whether PROC GLMSELECT can construct bootstrap confidence intervals for the predicted mean in a regression model, as described in
In ordinary least squares regression, there is an explicit formula for the confidence limit of the predicted mean. That is, for any observed value of the explanatory variables, you can create a 95% confidence interval (CI) for the predicted response. This formula assumes that the model is correctly specified and
A SAS programmer wanted to use PROC SGPLOT in SAS to visualize a regression model. The programmer wanted to visualize confidence limits for the predicted mean at certain values of the explanatory variable. This article shows two options for adding confidence limits to a scatter plot. You can use a
The acceptance-rejection method (sometimes called rejection sampling) is a method that enables you to generate a random sample from an arbitrary distribution by using only the probability density function (PDF). This is in contrast to the inverse CDF method, which uses the cumulative distribution function (CDF) to generate a random
There are dozens of common probability distributions for a continuous univariate random variable. Familiar examples include the normal, exponential, uniform, gamma, and beta distributions. Where did these distributions come from? Well, some mathematician needed a model for a stochastic process and wrote down the equation for the distribution, typically by
A previous article shows an example of a Markov chain model and computes the probability that the system ends up in a terminal state (called an absorbing state). As explained previously, you can often compute exact probabilities for questions about Markov chains. Nevertheless, it can be useful to know how
A previous article shows how to model the probabilities in a discrete-time Markov chain by using a Markov transition matrix. A Markov chain is a discrete-time stochastic process for which the current state of the system determines the probability of the next state. In this process, the probabilities for transitioning
While writing an article about labeling a polygon by using the centroid, I almost made a false claim about the centroid. I almost claimed that that the centroid is the point in a polygon that minimizes the sum of the distances to the vertices. It is not. The point that
A previous article explains the Spearman rank correlation, which is a robust cousin to the more familiar Pearson correlation. I've also discussed why you might want to use rank correlation, and how to interpret the strength of a rank correlation. This article gives a short example that helps you to
Since the COVID-19 pandemic began, video presentations and webcasts have become a regular routine for many of us. On days that I will be using my webcam, I wear a solid-color shirt. If I don't plan to be on camera, I can wear a pinstripe Oxford shirt. Why the difference?
Real-world data often exhibits extreme skewness. It is not unusual to have data span many orders of magnitude. Classic examples are the distributions of incomes (impoverished and billionaires) and population sizes (small countries and populous nations). The readership of books and blog posts show a similar distribution, which is sometimes
A previous article defines the silhouette statistic (Rousseeuw, 1987) and shows how to use it to identify observations in a cluster analysis that are potentially misclassified. The article provides many graphs, including the silhouette plot, which is a bar chart or histogram that displays the distribution of the silhouette statistic
In SAS, you can approximate the exponential of a matrix by using the EXPMATRIX function in SAS IML software. This article discusses the exponential of a matrix: what it is, how to compute it, why it is useful, and why you should think of it as a linear map that
In a previous article, I showed how to overlay a density estimate on a histogram by using the Graph Template Language (GTL). However, a SAS programmer asked how to overlay a curve on a histogram when the curve is not a density estimate. In this case, the vertical axis for
When the SAS statistical graphics (SG) procedures were designed in the early 2000s, a goal was to create a comprehensive Graph Template Language (GTL) and leverage the GTL by using SG procedures that perform common tasks easily without having to write any GTL. This project was hugely successful, and "ODS
A previous article discusses how to compute the union, intersection, and other subsets of a pair of sets. In that article, I displayed a simple Venn diagram (reproduced to the right) that illustrates the intersection and difference between two sets. The diagram uses a red disk for one set, a
The "Teacher’s Corner" of The American Statistician enables statisticians to discuss topics that are relevant to teaching and learning statistics. Sometimes, the articles have practical relevance, too. Andersson (2023) "The Wald Confidence Interval for a Binomial p as an Illuminating 'Bad' Example," is intended for professors and masters-level students in
A SAS user asked how to interpret a rank-based correlation such as a Spearman correlation or a Kendall correlation. These are alternative measures to the usual Pearson product-moment correlation, which is widely used. The programmer knew that words like "weak," "moderate," and "strong" are sometimes used to describe the Pearson
A previous article discusses the issue of a confounding variable and uses correlation to give an example. The example shows that the correlation between two variables might be affected by a third variable, which is called a confounding variable. The article mentions that you can use the PARTIAL statement in
A data analyst wanted to estimate the correlation between two variables, but he was concerned about the influence of a confounding variable that is correlated with them. The correlation might affect the apparent relationship between main two variables in the study. A common confounding variable is age because young people
A previous article describes the metalog distribution (Keelin, 2016). The metalog distribution is a flexible family of distributions that can model a wide range of shapes for data distributions. The metalog system can model bounded, semibounded, and unbounded continuous distributions. This article shows how to use the metalog distribution in
A SAS programmer wanted to compute the distribution of X-Y, where X and Y are two beta-distributed random variables. Pham-Gia and Turkkan (1993) derive a formula for the PDF of this distribution. Unfortunately, the PDF involves evaluating a two-dimensional generalized hypergeometric function, which is not available in all programming languages.
A SAS programmer asked for help to simulate data from a distribution that has certain properties. The distribution must be supported on the interval [a, b] and have a specified mean, μ, where a < μ < b. It turns out that there are infinitely many distributions that satisfy these
SAS programmers love to make special graphs for Valentine's Day. In fact, there is a long history of heart-shaped graphs and love-inspired programs written in SAS! Last year, I added to the collection by showing how a ball bounces on a heart-shaped billiards table. This year, I create a similar
Did you know that about 8% of the world's men are colorblind? (More correctly, 8% of men are "color vision deficient," since they see colors, but not all colors.) Because of the "birthday paradox," in a room that contains eight men, the probability is 50% that at least one is
A previous article shows that you can use the Intercept parameter to control the ratio of events to nonevents in a simulation of data from a logistic regression model. If you decrease the intercept parameter, the probability of the event decreases; if you increase the intercept parameter, the probability of
This article shows that you can use the intercept parameter to control the probability of the event in a simulation study that involves a binary logistic regression model. For simplicity, I will simulate data from a logistic regression model that involves only one explanatory variable, but the main idea applies
SAS' Sylvia Kabisa shows you how an online media company might use SAS to offer targeted discounts through personalized pricing.
Last year, I wrote almost 90 articles for The DO Loop blog. My most popular articles were about SAS programming, data visualization, statistics and data analysis, and matrix computations. If you missed these articles when I published them—or if you want to read them again!— here is the "Reader's Choice
