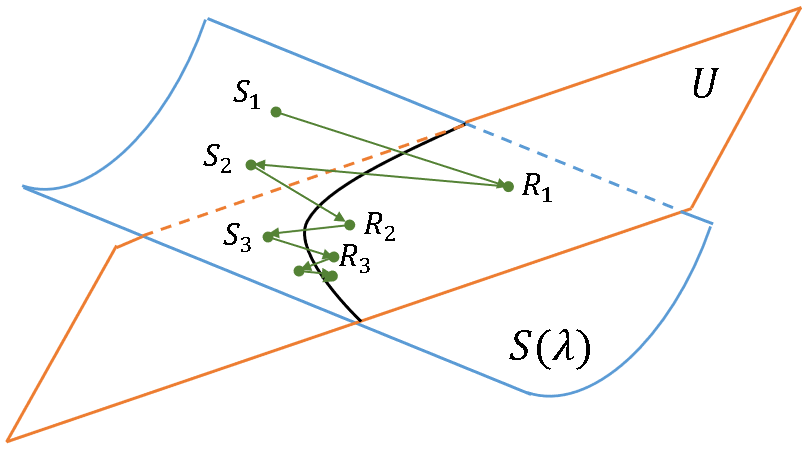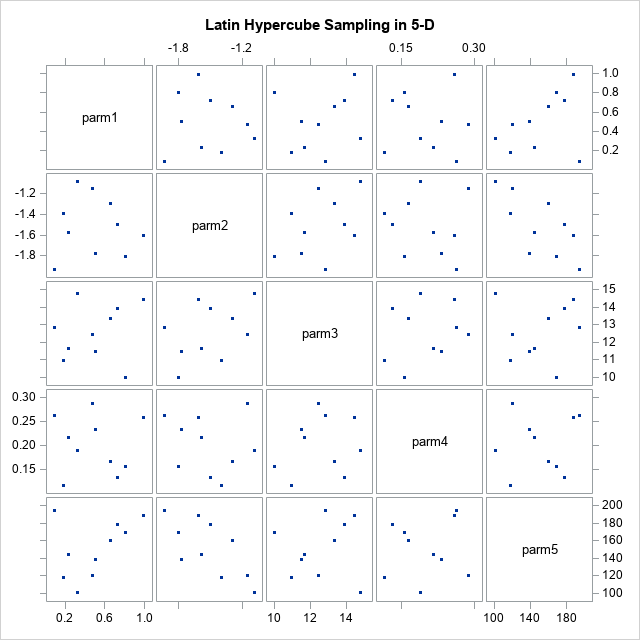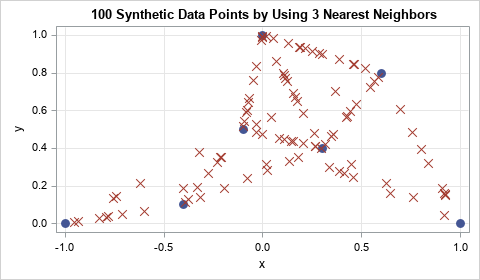
The Synthetic Minority Over-sampling Technique (SMOTE) was created to address class-imbalance problems in machine learning algorithms. The idea is to oversample from the rare events prior to running a machine learning classification algorithm. However, at its heart, the SMOTE algorithm (Chawla et al., 2002) is essentially a way to simulate