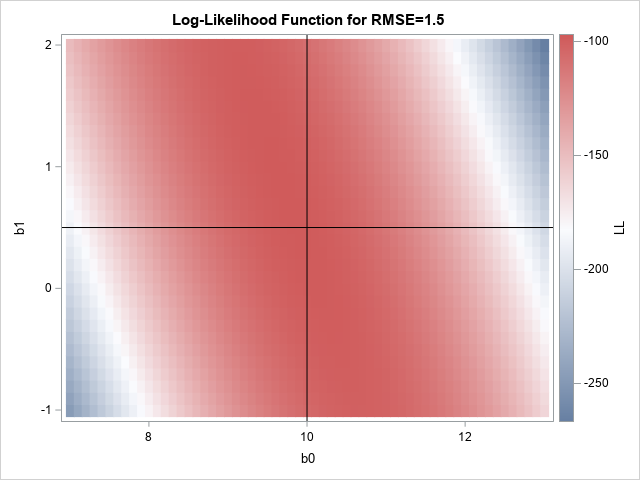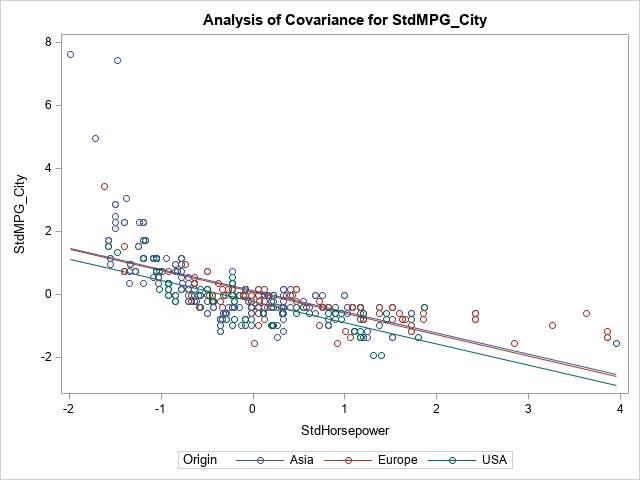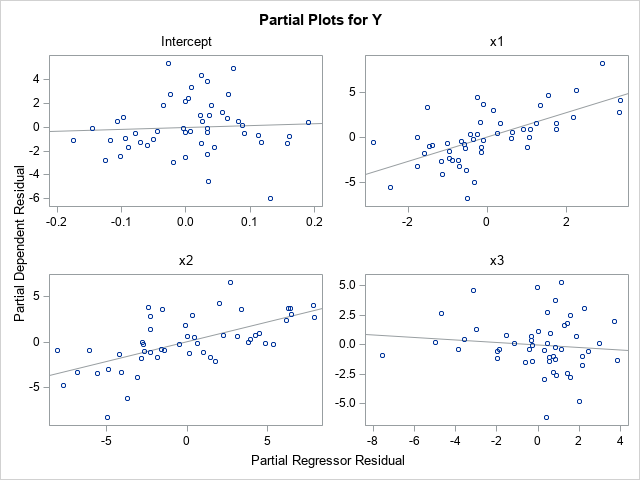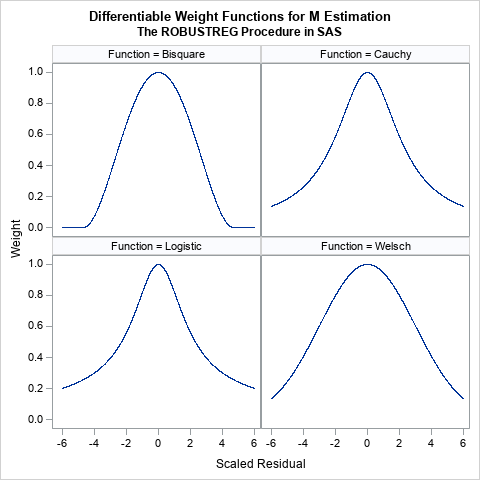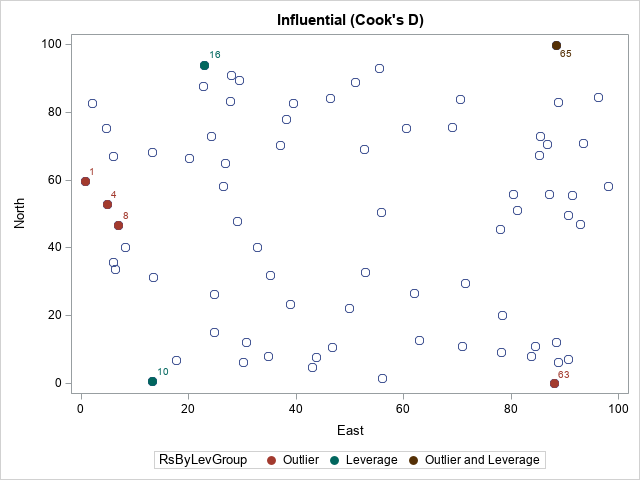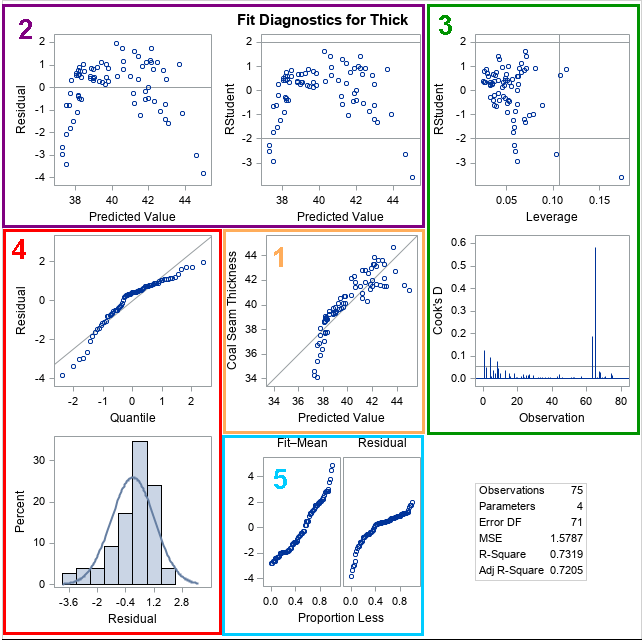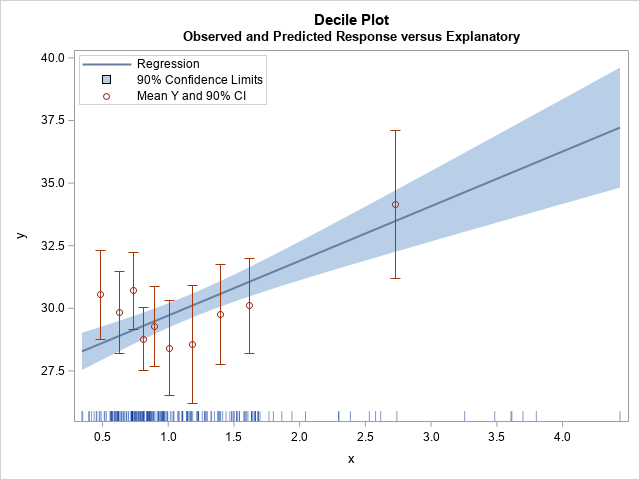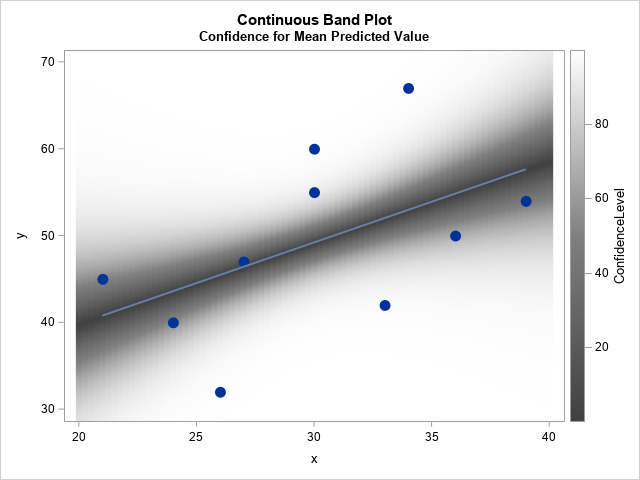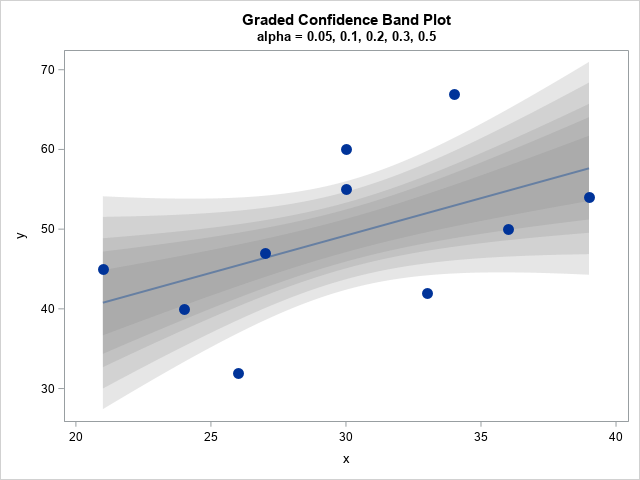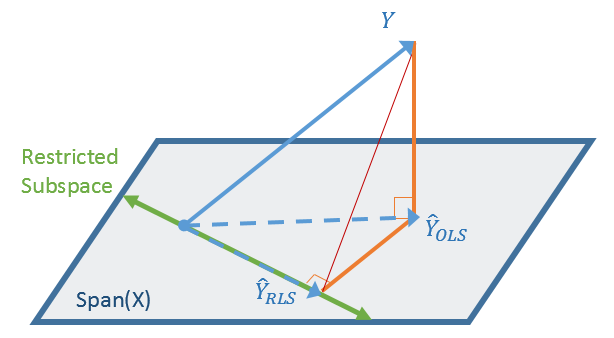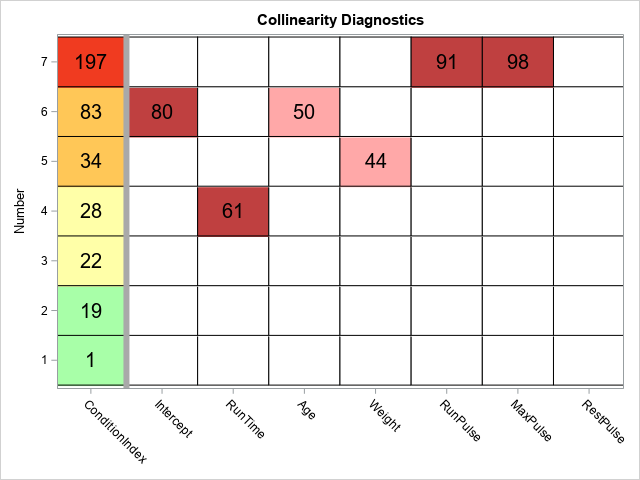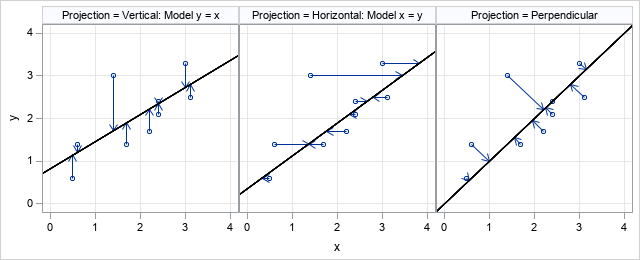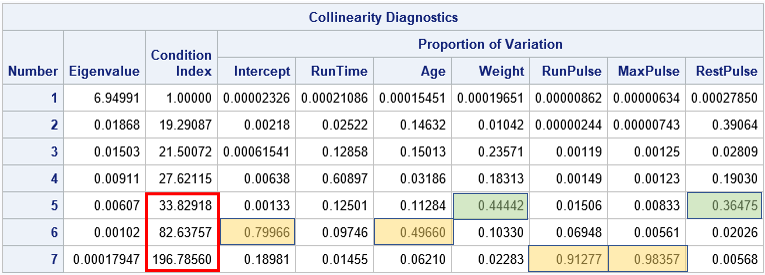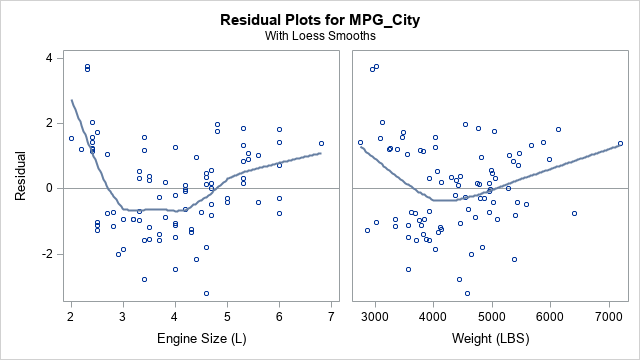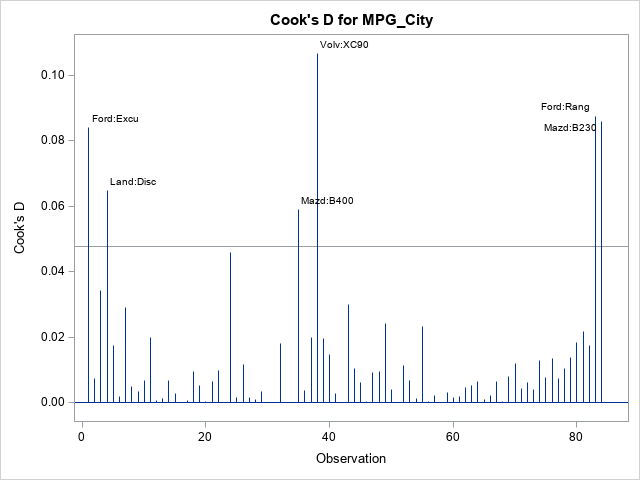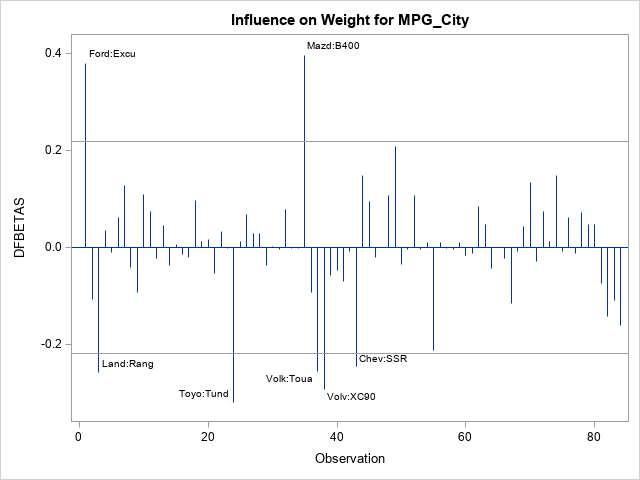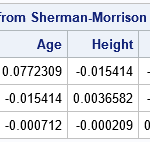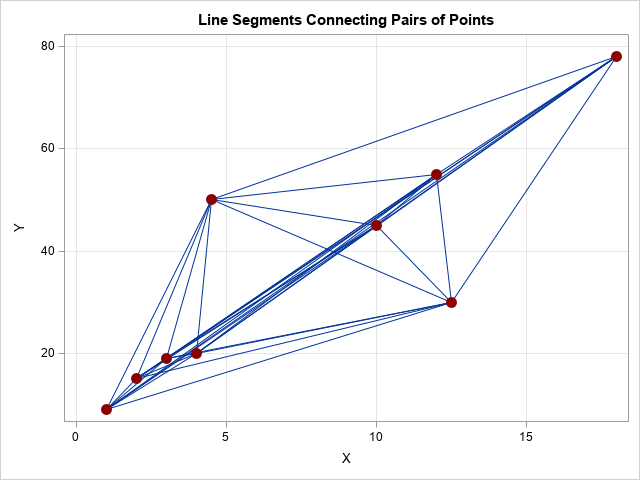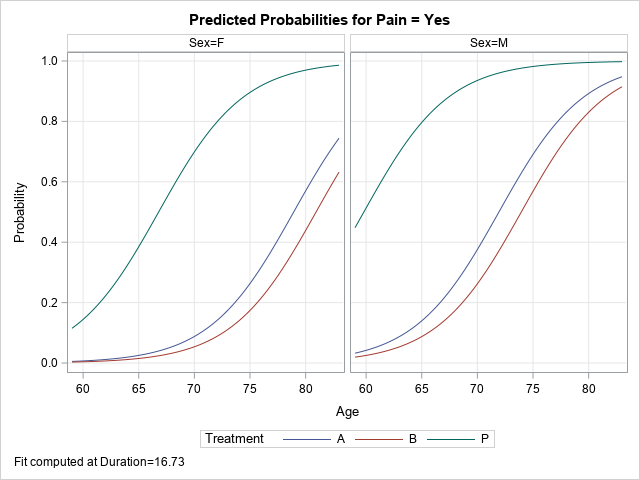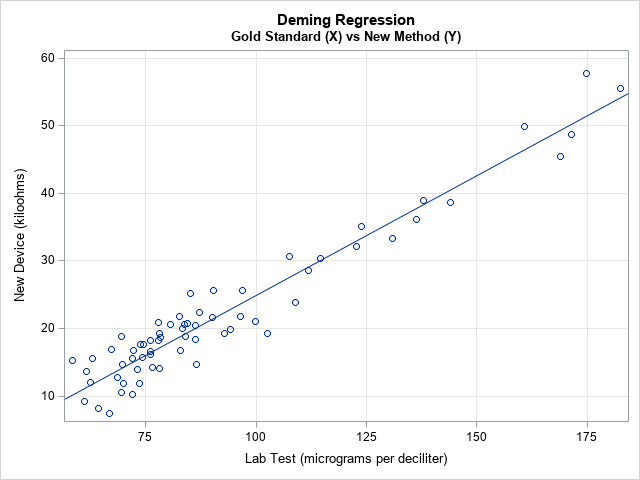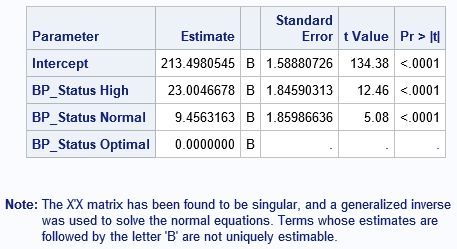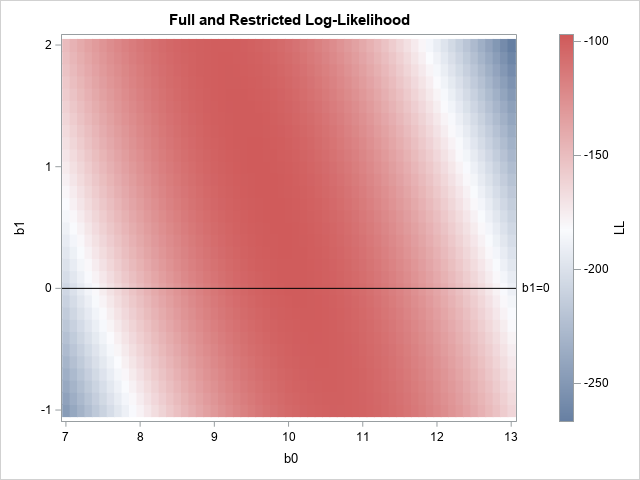
A recent article describes how to estimate coefficients in a simple linear regression model by using maximum likelihood estimation (MLE). One of the nice properties of an MLE formulation is that you can compare a large model with a nested submodel in a natural way. For example, if you can
A statistical analyst used the GENMOD procedure in SAS to fit a linear regression model. He noticed that the table of parameter estimates has an extra row (labeled "Scale") that is not a regression coefficient. The "scale parameter" is not part of the parameter estimates table produced by PROC REG
A previous article discusses standardized coefficients in linear regression models and shows how to compute standardized regression coefficients in SAS by using the STB option on the MODEL statement in PROC REG. It also discusses how to interpret a standardized regression coefficient. Recently, a SAS user wanted to know how
