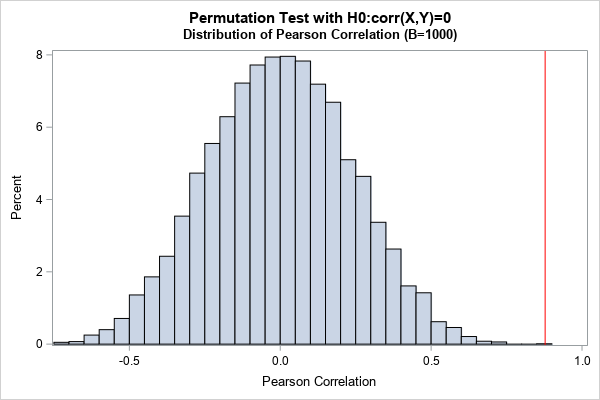
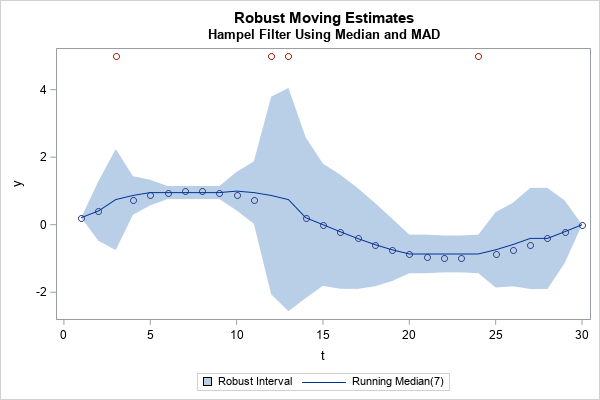
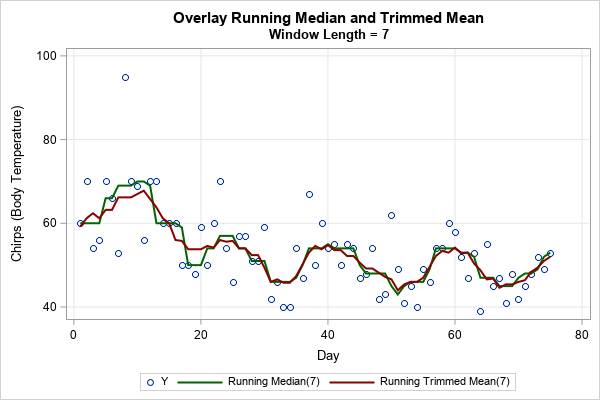
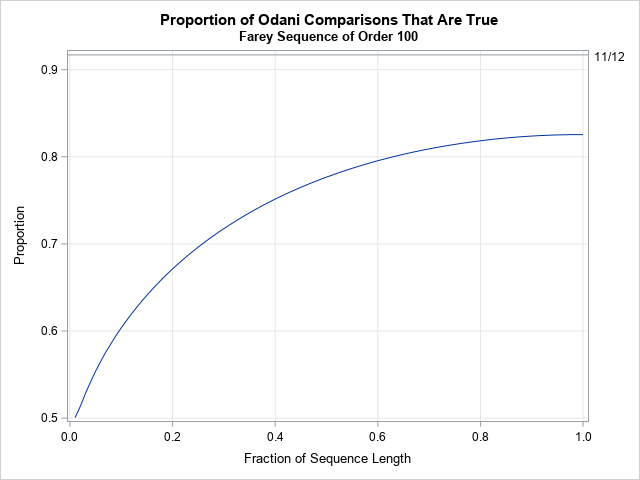
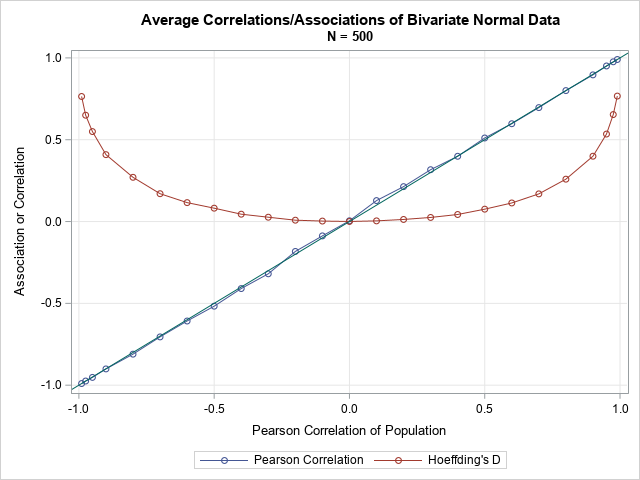
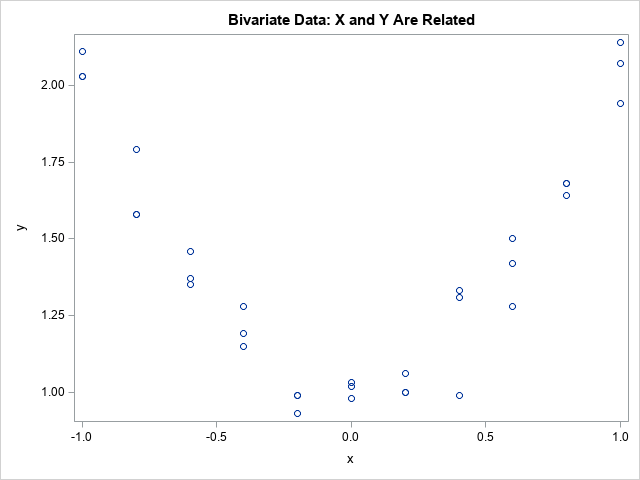
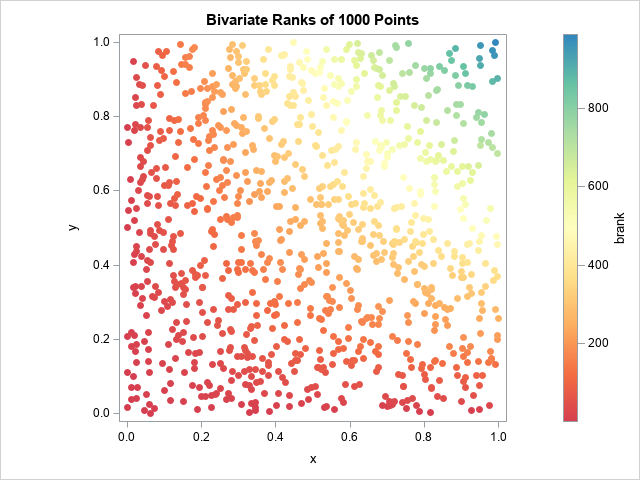
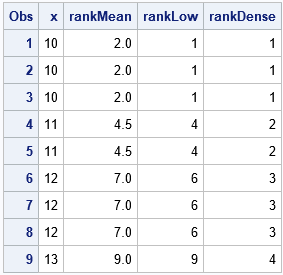
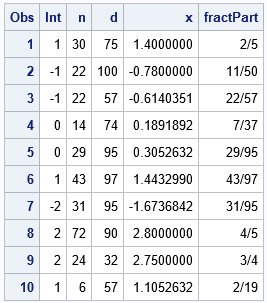
Many nonparametric statistical methods use the ranks of observations to compute distribution-free statistics. In SAS, two procedures that use ranks are PROC NPAR1WAY and PROC CORR. Whereas the SPEARMAN option in PROC CORR (which computes rank correlation) uses only the "raw" tied ranks, PROC NPAR1WAY uses transformations of the ranks,