The SAS Data Science Blog
Advanced analytics from SAS data scientists
Authors: Steven Harenberg and Amy Becker The total solar eclipse taking place across a thin band of the United States on April 8, 2024, is going to be a stellar event. In this post, we will help plan a journey to see the total solar eclipse. We will use algorithms
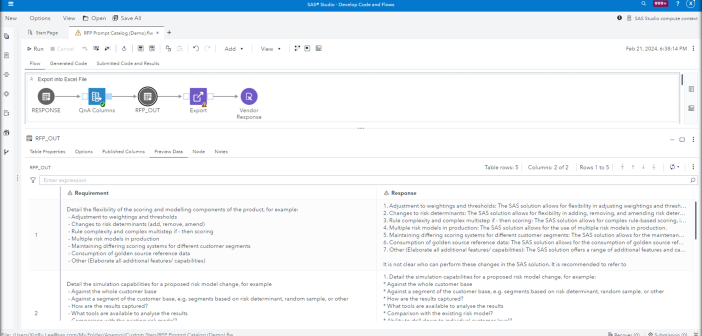
SAS Viya can allow users and organizations to more easily interface with the LLM application, build better prompts and evaluate systematically which of these prompts leads to the best responses to ensure the best outcomes.

SAS' Varun Valsaraj demonstrates how to build a digital assistant for a warehouse space optimization use case.

SAS' Julia Moreno shows you how to use generative AI to build a digital assistant that interacts with a model using natural language conversation.

The National Institute of Standards and Technology (NIST) has released a set of standards and best practices within their AI Risk Management Framework for building responsible AI systems. NIST sits under the U.S. Department of Commerce and their mission is to promote innovation and industrial competitiveness. NIST offers a portfolio

Can we use Computer Vision (CV) to recognize the identity of over 500 Galapagos sea turtles by using just an image? This was the question asked of SAS by researchers at the Galapagos Science Center (GSC), a joint partnership between the University of North Carolina at Chapel Hill’s (UNC) Center for





