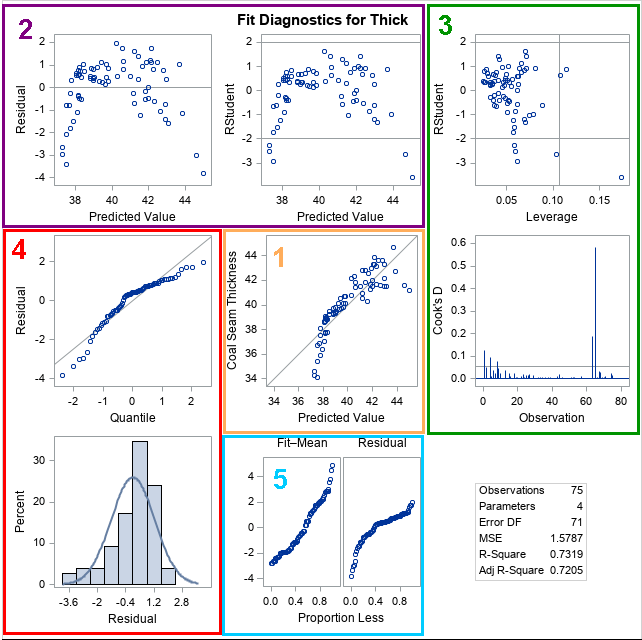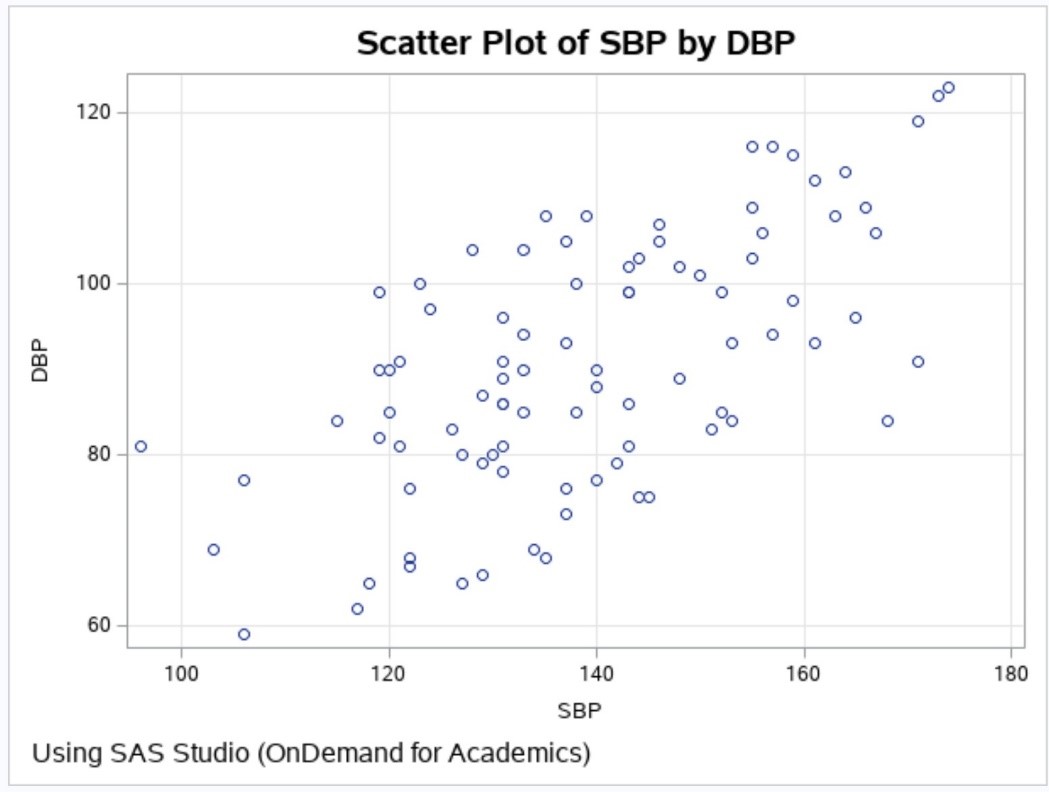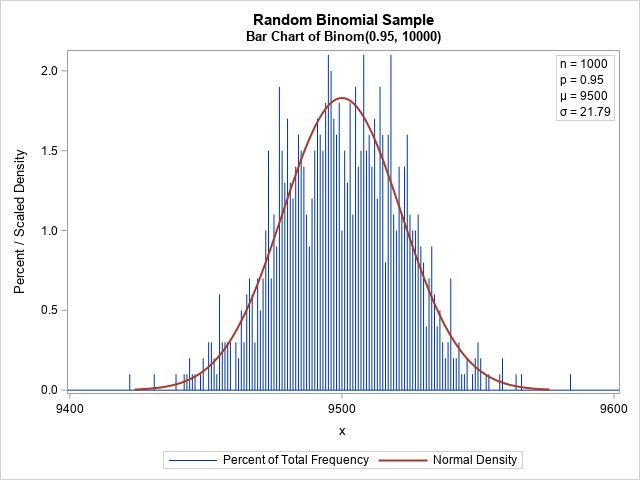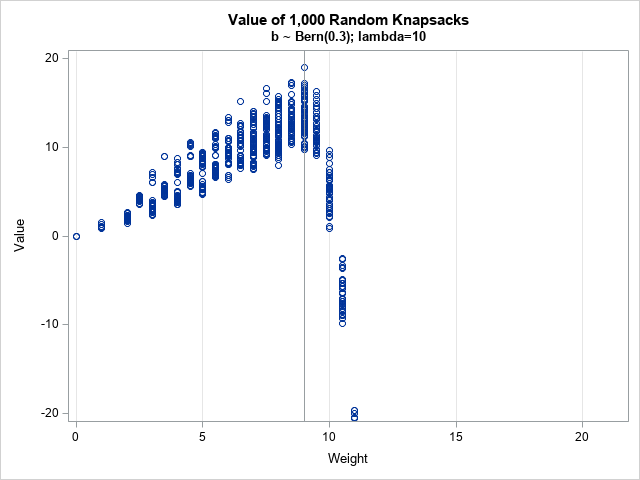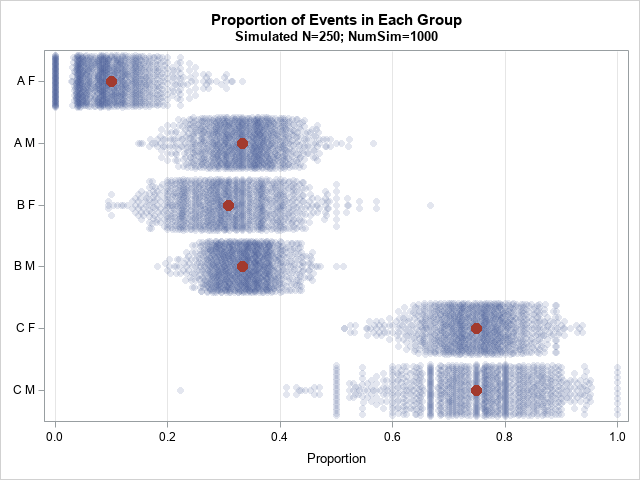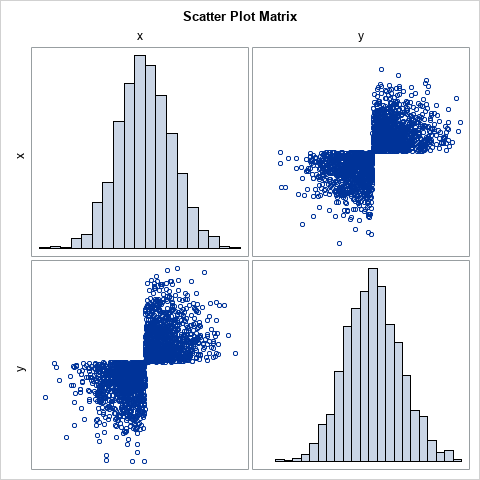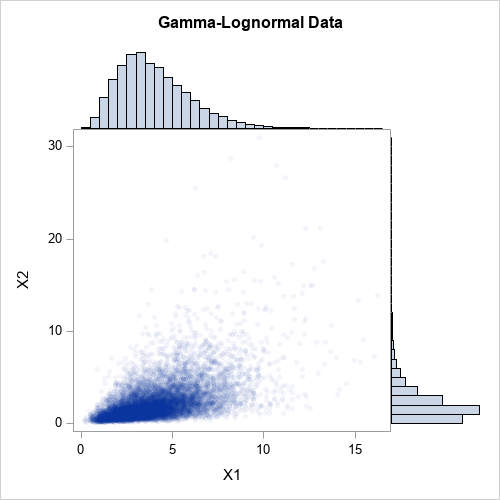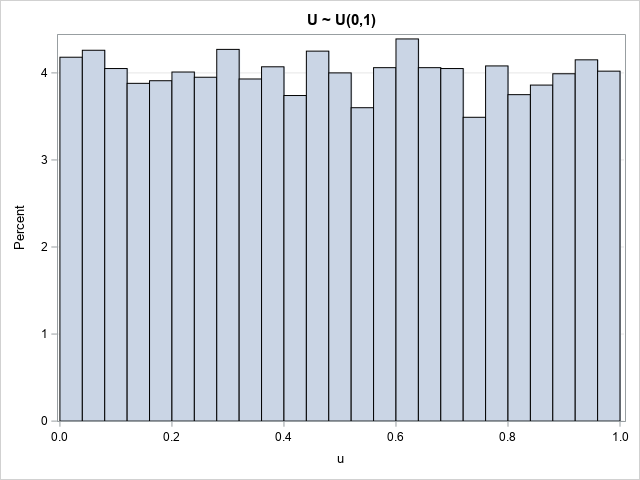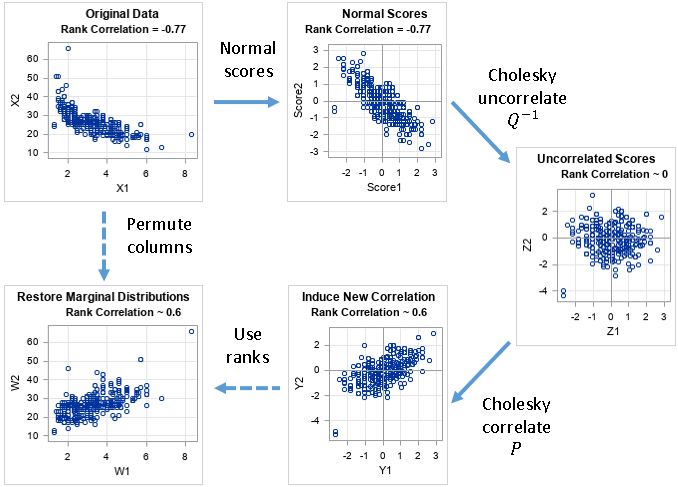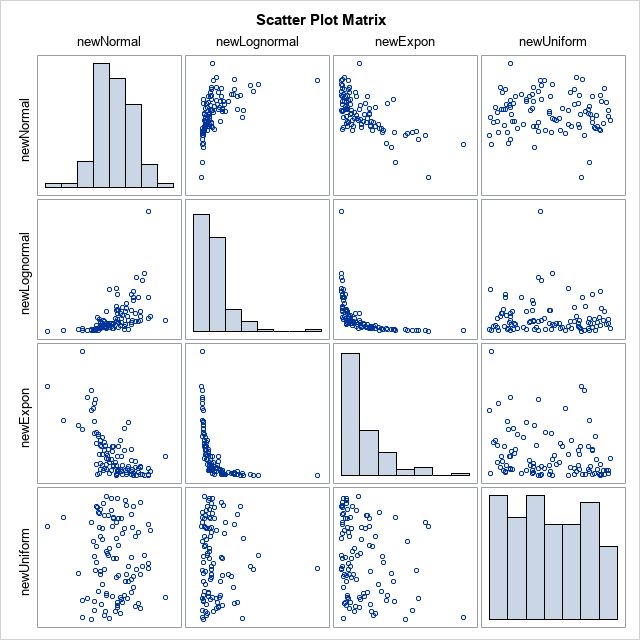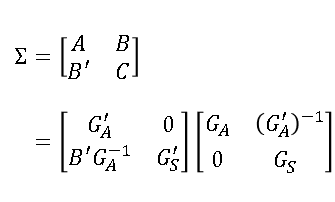
You can use the Cholesky decomposition of a covariance matrix to simulate data from a correlated multivariate normal distribution. This method is encapsulated in the RANDNORMAL function in SAS/IML software, but you can also perform the computations manually by calling the ROOT function to get the Cholesky root and then
Last year, I wrote almost 100 posts for The DO Loop blog. My most popular articles were about data visualization, statistics and data analysis, and simulation and bootstrapping. If you missed any of these gems when they were first published, here are some of the most popular articles from 2021:
There is no shortage of challenges associated with the deployment of AI: a lack of access to infrastructure, a lack of skills, and new legislation meant to enforce the responsible use of this evolving technology. But the most consequential questions facing us are innately human. Namely, ensuring human agency, safety
While discussing how to compute convex hulls in SAS with a colleague, we wondered how the size of the convex hull compares to the size of the sample. For most distributions of points, I claimed that the size of the convex hull is much less than the size of the
This blog is a continuation of a previous blog that discussed creating simulated data sets. If you have not seen it, you might want to review it, especially if you are not familiar with the RAND function. The program that I'm going to show you simulates a drug study with
Recall that the binomial distribution is the distribution of the number of successes in a set of independent Bernoulli trials, each having the same probability of success. Most introductory statistics textbooks discuss the approximation of the binomial distribution by the normal distribution. The graph to the right shows that the
There are times when it is useful to simulate data. One of the reasons I use simulated data sets is to demonstrate statistical techniques such as multiple or logistic regression. By using SAS random functions and some DATA step logic, you can create variables that follow certain distributions or are
A previous article discusses how to use SAS regression procedures to fit a two-parameter Weibull distribution in SAS. The article shows how to convert the regression output into the more familiar scale and shape parameters for the Weibull probability distribution, which are fit by using PROC UNIVARIATE. Although PROC UNIVARIATE
SAS' Bahar Biller, an operations researcher, details how to develop a supply chain digital twin.
Sometimes we can learn as much from our mistakes as we do from our successes. Recently, I needed to solve an optimization problem for which the solution vector was a binary vector subject to a constraint. I was in a hurry. Without thinking much about what I was doing, I
Tropical Storm Ana, which formed in May this year, officially made 2021 the seventh consecutive year that a storm formed before the season's designated start. Since then we have seen a number of storms, representative of an increase of severe weather over the past few years, especially as we remember
A statistical programmer asked how to simulate event-trials data for groups. The subjects in each group have a different probability of experiencing the event. This article describes one way to simulate this scenario. The simulation is similar to simulating from a mixture distribution. This article also shows three different ways
As an example, when using ordinary least squares regression (OLS), if your response or dependent attribute’s residuals are not normally distributed, your analysis is likely going to be affected and typically not in a good way. The farther away your input data is from normality, the impact on your model
A conversation with BASF, Damien Caby, Senior Vice President, who is responsible for the global business unit Oilfield & Mining Solutions.
After my recent articles on simulating data by using copulas, many readers commented about the power of copulas. Yes, they are powerful, and the geometry of copulas is beautiful. However, it is important to be aware of the limitations of copulas. This article creates a bizarre example of bivariate data,
In general, it is hard to simulate multivariate data that has a specified correlation structure. Copulas make that task easier for continuous distributions. A previous article presented the geometry behind a copula and explained copulas in an intuitive way. Although I strongly believe that statistical practitioners should be familiar with
Do you know what a copula is? It is a popular way to simulate multivariate correlated data. The literature for copulas is mathematically formidable, but this article provides an intuitive introduction to copulas by describing the geometry of the transformations that are involved in the simulation process. Although there are
This article uses simulation to demonstrate the fact that any continuous distribution can be transformed into the uniform distribution on (0,1). The function that performs this transformation is a familiar one: it is the cumulative distribution function (CDF). A continuous CDF is defined as an integral, so the transformation is
Le développement de l’intelligence artificielle dans les différents secteurs d’activité fait de plus en plus l'objet d'une surveillance accrue en raison de l’aptitude des algorithmes à amplifier les bonnes et les mauvaises décisions. En parallèle, les discussions sur l'éthique (règles de conduite reflétant nos croyances sur ce qui est juste
A previous article showed how to simulate multivariate correlated data by using the Iman-Conover transformation (Iman and Conover, 1982). The transformation preserves the marginal distributions of the original data but permutes the values (columnwise) to induce a new correlation among the variables. When I first read about the Iman-Conover transformation,
Simulating univariate data is relatively easy. Simulating multivariate data is much harder. The main difficulty is to generate variables that have given univariate distributions but also are correlated with each other according to a specified correlation matrix. However, Iman and Conover (1982, "A distribution-free approach to inducing rank correlation among
It’s not too late to register for Tuesday’s (May 18) SAS Global Forum kickoff. And there are so many online sessions it’s going to be hard to choose which to attend. Business and analytics experts are leading dozens of virtual session for industries, from agtech, banking and financial services, goverment,
Odani's truism is a mathematical result that says that if you want to compare the fractions a/b and c/d, it often is sufficient to compare the sums (a+d) and (b+c) rather than the products a*d and b*c. (All of the integers a, b, c, and d are positive.) If you
Quick! Which fraction is bigger, 40/83 or 27/56? It's not always easy to mentally compare two fractions to determine which is larger. For this example, you can easily see that both fractions are a little less than 1/2, but to compare the numbers you need to compare the products 40*56
As mentioned in my article about Monte Carlo estimate of (one-dimensional) integrals, one of the advantages of Monte Carlo integration is that you can perform multivariate integrals on complicated regions. This article demonstrates how to use SAS to obtain a Monte Carlo estimate of a double integral over rectangular and
A previous article shows how to use Monte Carlo simulation to estimate a one-dimensional integral on a finite interval. A larger random sample will (on average) result in an estimate that is closer to the true value of the integral than a smaller sample. This article shows how you can
Ein Gespräch mit Broetje-Automation: Dirk Eickhorst, Leiter Robotik.
I recently learned about a new feature in PROC QUANTREG that was added in SAS/STAT 15.1 (part of SAS 9.4M6). Recall that PROC QUANTREG enables you to perform quantile regression in SAS. (If you are not familiar with quantile regression, see an earlier article that describes quantile regression and provides
I've previously written about how to generate all pairwise interactions for a regression model in SAS. For a model that contains continuous effects, the easiest way is to use the EFFECT statement in PROC GLMSELECT to generate second-degree "polynomial effects." However, a SAS programmer was running a simulation study and
Note from Udo Sglavo on mathematical optimization: When data scientists look at the essence of analytics and wonder about their daily endeavor, it often comes down to supporting better decisions. Peter F. Drucker, the founder of modern management, stated: "Whenever you see a successful business, someone once made a courageous decision."
