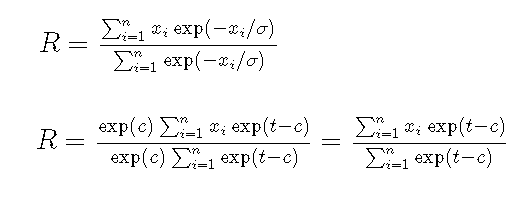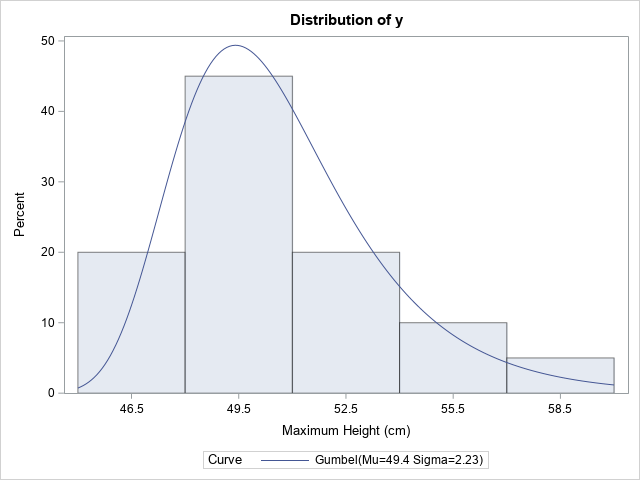
SAS provides procedures to fit common probability distributions to sample data. You can use PROC UNIVARIATE in Base SAS or PROC SEVERITY in SAS/ETS software to estimate the distribution parameters for approximately 20 common distributions, including normal, lognormal, beta, gamma, and Weibull. Since there are infinitely many distributions, you may