The Raleigh News & Observer published a front-page article about the effect of wealth and poverty on high school athletics in North Carolina. In particular, the article concluded that "high schools with a high percentage of poor students rarely win titles in the so-called country club sports—tennis, golf and swimming—and
My colleague Robert Allison finds the most interesting data sets to visualize! Yesterday he posted a visualization of toothless seniors in the US. More precisely, he created graphs that show the estimated prevalence of adults (65 years or older) who have had all their natural teeth extracted. The dental profession
My son is in high school and plans to take the ACT, a standardized test to assess college aptitude and readiness. My wife asked, "What is a good score for the ACT?" I didn't know, but I did a quick internet search and discovered a tabulation of scores for the
Recently a SAS customer asked how to Winsorize data in SAS. Winsorization is best known as a way to construct robust univariate statistics. The Winsorized mean is a robust estimate of location. The Winsorized mean is similar to the trimmed mean, and both are described in the documentation for PROC
When you count the outcomes of an experiment, you do not always observe all of the possible outcomes. For example, if you roll a six-sided die 10 times, it might be that the "1" face does not appear in those 10 rolls. Obviously, this situation occurs more frequently with small
"Daddy, help! Help me! Come quick!" I heard my daughter's screams from the upstairs bathroom and bounded up the stairs two at a time. Was she hurt? Bleeding? Was the toilet overflowing? When I arrived in the doorway, she pointed at the wall and at the floor. The wall was
I was reading a statistics book when I encountered a histogram that caught my eye. The histogram looked similar to the one at the left. It contained a normal density estimate overlaid on a histogram, but the height of the density curve seemed too short when compared to the heights
A SAS programmer asked for a list of SAS/IML functions that operate on the columns of an n x p matrix and return a 1 x p row vector of results. The functions that behave this way tend to compute univariate descriptive statistics such as the mean, median, standard deviation, and quantiles. The following
Perhaps you saw the headlines earlier this week about the fact that it has been nine years since the last major hurricane (category 3, 4, or 5) hit the US coast. According to a post on the GeoSpace blog, which is published by the American Geophysical Union (AGU), researchers ran
Suppose that you compute the correlation matrix (call it R1) for a set of variables x1, x2, ..., x8. For some reason, you later want to compute the correlation matrix for the variables in a different order, maybe x2, x1, x7,..., x6. Do you need to go back to the
Imagine that you have one million rows of numerical data and you want to determine if a particular "target" value occurs. How might you find where the value occurs? For univariate data, this is an easy problem. In the SAS DATA step you can use a WHERE clause or a
Saturday, March 14, 2015, is Pi Day, and this year is a super-special Pi Day! This is your once-in-a-lifetime chance to celebrate the first 10 digits of pi (π) by doing something special on 3/14/15 at 9:26:53. Apologies to my European friends, but Pi Day requires that you represent dates
I recently wrote about how to overlay multiple curves on a single graph by reshaping wide data (with many variables) into long data (with a grouping variable). The implementation used PROC TRANSPOSE, which is a procedure in Base SAS. When you program in the SAS/IML language, you might encounter data
Data. To a statistician, data are the observed values. To a SAS programmer, analyzing data requires knowledge of the values and how the data are arranged in a data set. Sometimes the data are in a "wide form" in which there are many variables. However, to perform a certain analysis
I published 118 blog posts in 2014. This article presents my most popular posts from 2014 and late 2013. 2014 will always be a special year for me because it was the year that the SAS University Edition was launched. The University Edition means that SAS/IML is available to all
My colleagues at the SAS & R blog recently posted an example of how to program a permutation test in SAS and R. Their SAS implementation used Base SAS and was "relatively cumbersome" (their words) when compared with the R code. In today's post I implement the permutation test in
My colleague Robert Allison has a knack for finding fascinating data. Last week he did it again by locating data about how blood types and Rh factors vary among countries. He produced a series of eight world maps, each showing the prevalence of a blood type (A+, A-, B+, B-,
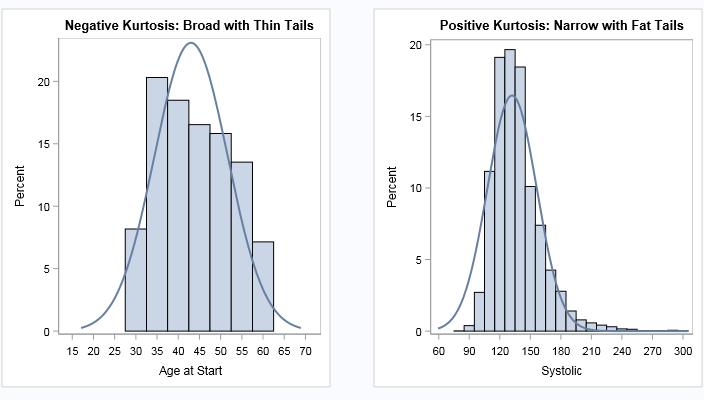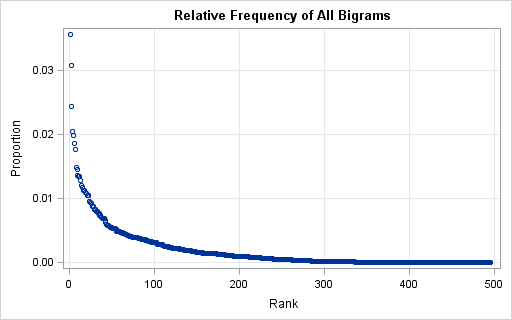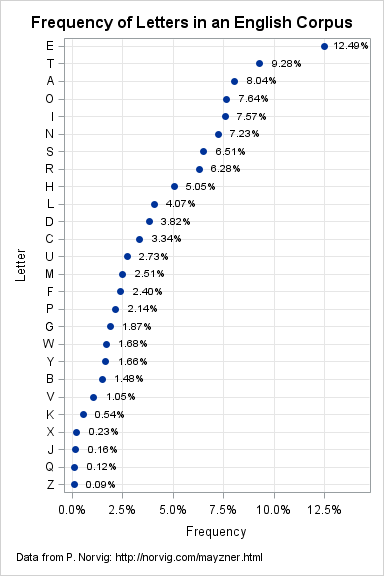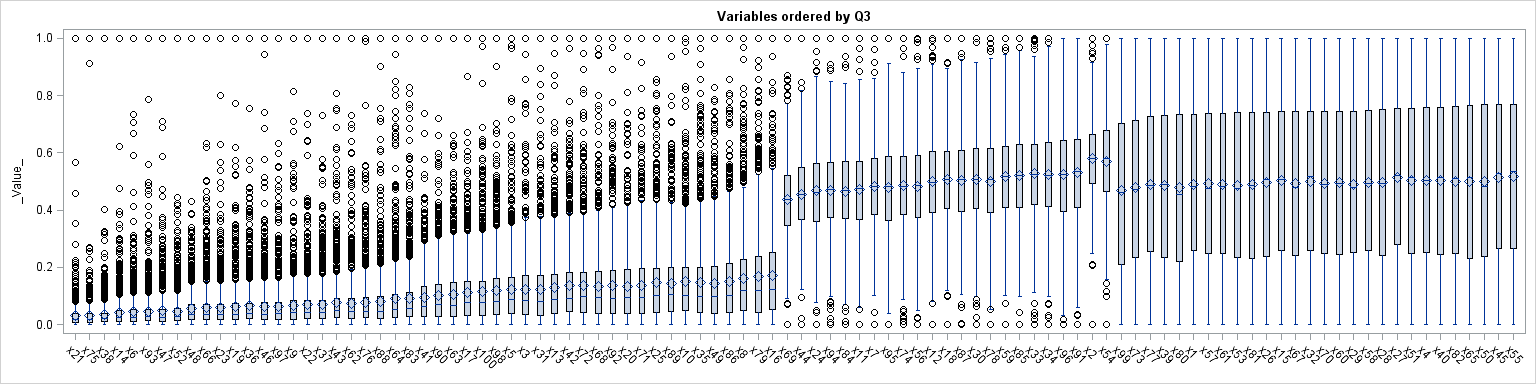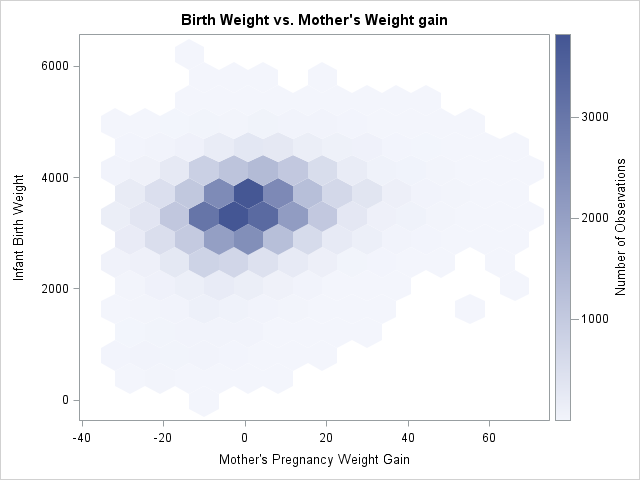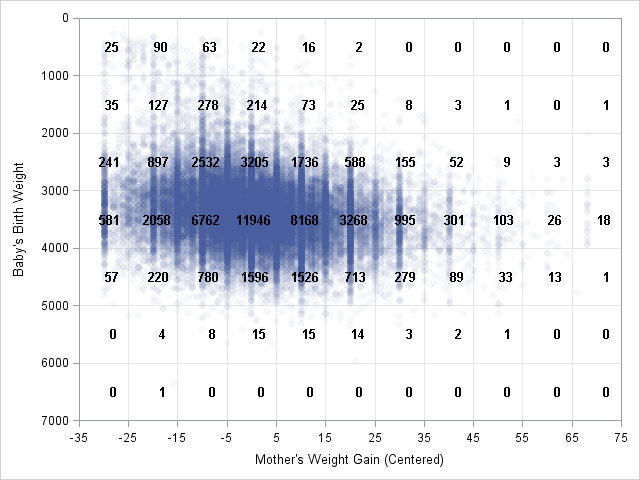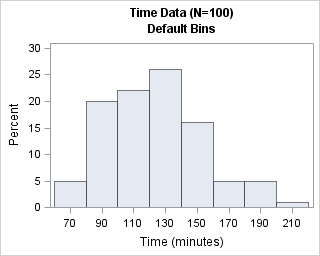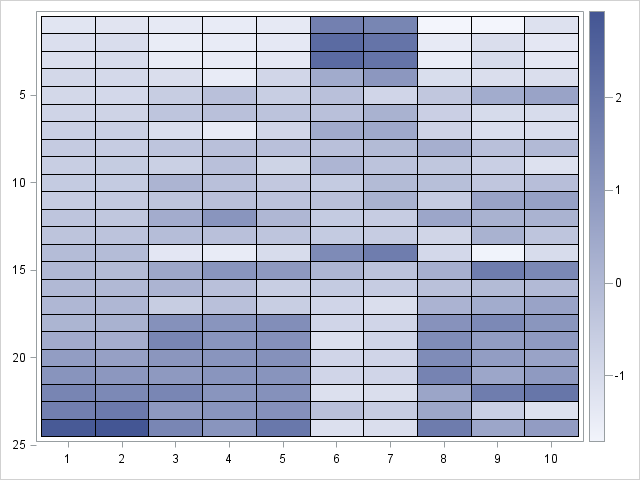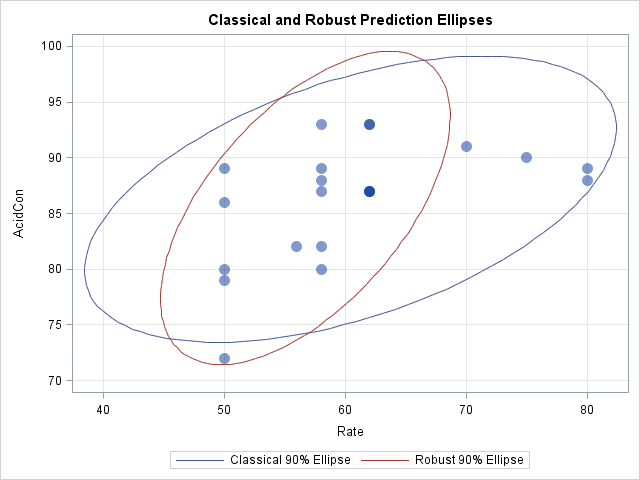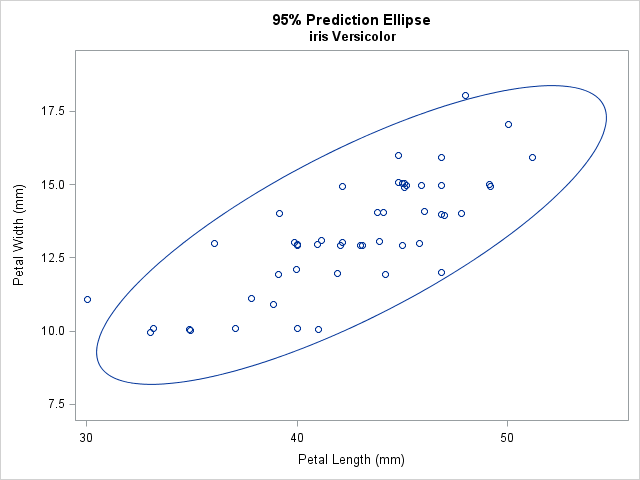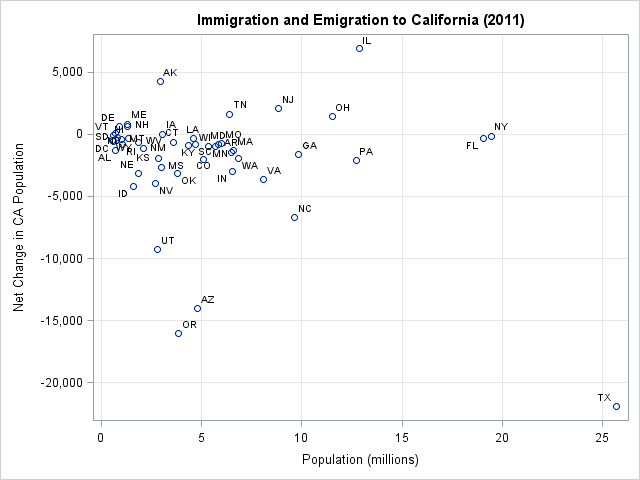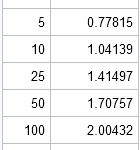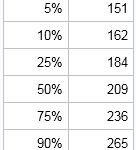
In my article about how to create a quantile plot, I chose not to discuss a theoretical issue that occasionally occurs. The issue is that for discrete data (which includes rounded values), it might be impossible to use quantile values to split the data into k groups where each group
What is kurtosis? What does negative or positive kurtosis mean, and why should you care? How do you compute kurtosis in SAS software? It is not clear from the definition of kurtosis what (if anything) kurtosis tells us about the shape of a distribution, or why kurtosis is relevant to
It usually takes more than three weeks to prepare a good impromptu speech. --Mark Twain In the popular Cryptoquote puzzle, you are presented with an enciphered version of a quote by a famous person. One of the appeals of the puzzle for me is reading the deciphered quote, such
Double, double toil and trouble; Fire burn, and caldron bubble. Macbeth, Act IV, Scene I For the cyptanalyst or recreational puzzle solver, "double double" does not lead to toil or trouble. Just the opposite: The occurrence of a double-letter bigram in an enciphered word puzzle is quite fortunate. Certain double
In a previous article I introduced the HEATMAPCONT subroutine in SAS/IML 13.1, which makes it easy to visualize matrices by using heat maps with continuous color ramps. This article introduces a companion subroutine. The HEATMAPDISC subroutine, which also requires SAS/IML 13.1, is designed to visualize matrices that have a small
In last week's article about the distribution of letters in an English corpus, I presented research results by Peter Norvig who used Google's digitized library and tabulated the frequency of each letter. Norvig also tabulated the frequency of bigrams, which are pairs of letters that appear consecutively within a word.
While at JSM 2014 in Boston, a statistician asked me whether it was possible to create a "customized bin plot" in SAS. When I asked for more information, she told me that she has a large data set. She wants to visualize the data, but a scatter plot is not
The skewness of a distribution indicates whether a distribution is symmetric or not. A distribution that is symmetric about its mean has zero skewness. In contrast, if the right tail of a unimodal distribution has more mass than the left tail, then the distribution is said to be "right skewed"
It's time for another blog post about ciphers. As I indicated in my previous blog post about substitution ciphers, the classical substitution cipher is no longer used to encrypt ultra-secret messages because the enciphered text is prone to a type of statistical attack known as frequency analysis. At the root
In a previous blog post I showed how to order a set of variables by a statistic. After reshaping data, you can create a graph that contains box plots for many variables. Ordering the variables by some statistic (mean, median, variance,...) helps to differentiate and distinguish the variables. You can
While I was working on my recent blog post about two-dimensional binning, a colleague asked whether I would be discussing "the new hexagonal binning method that was added to the SURVEYREG procedure in SAS/STAT 13.2." I was intrigued: I was not aware that hexagonal binning had been added to a
Last Monday I discussed how to choose the bin width and location for a histogram in SAS. The height of each histogram bar shows the number of observations in each bin. Although my recent article didn't mention it, you can also use the IML procedure to count the number of
When you create a histogram with statistical software, the software uses the data (including the sample size) to automatically choose the width and location of the histogram bins. The resulting histogram is an attempt to balance statistical considerations, such as estimating the underlying density, and "human considerations," such as choosing
