My wife got one of those electronic activity trackers a few months ago and has been diligently walking every day since then. At the end of the day she sometimes reads off how many steps she walked, as measured by her activity tracker. I am always impressed at how many
In a previous blog post, I showed how to use the graph template language (GTL) in SAS to create heat maps with a continuous color ramp. SAS/IML 13.1 includes the HEATMAPCONT subroutine, which makes it easy to create heat maps with continuous color ramps from SAS/IML matrices. Typical usage includes
In a previous blog post, I showed how to overlay a prediction ellipse on a scatter plot in SAS by using the ELLIPSE statement in PROC SGPLOT. The ELLIPSE statement draws the ellipse by using a standard technique that assumes the sample is bivariate normal. Today's article describes the technique
It is common in statistical graphics to overlay a prediction ellipse on a scatter plot. This article describes two easy ways to overlay prediction ellipses on a scatter plot by using SAS software. It also describes how to overlay multiple prediction ellipses for subpopulations. What is a prediction ellipse? A
An empty matrix is a matrix that has zero rows and zero columns. At first "empty matrix" sounds like an oxymoron, but when programming in a matrix language such as SAS/IML, empty matrices arise surprisingly often. Sometimes empty matrices occur because of a typographical error in your program. If you
In my four years of blogging, the post that has generated the most comments is "How to handle negative values in log transformations." Many people have written to describe data that contain negative values and to ask for advice about how to log-transform the data. Today I describe a transformation
In my previous blog post, I showed how to use log axes on a scatter plot in SAS to better visualize data that range over several orders of magnitude. Because the data contained counts (some of which were zero), I used a custom transformation x → log10(x+1) to visualize the
If you are trying to visualize numerical data that range over several magnitudes, conventional wisdom says that a log transformation of the data can often result in a better visualization. This article shows several ways to create a scatter plot with logarithmic axes in SAS and discusses some of the
A few years ago I blogged about how to expand a data set by using a frequency variable. The DATA step in the article was simple, but the SAS/IML function was somewhat complicated and used a DO loop to expand the data. (Although a reader later showed how to avoid
Last week I showed how to use the SUBMIT and ENDSUBMIT statements in the SAS/IML language to call the SGPLOT procedure to create ODS graphs of data that are in SAS/IML vectors and matrices. I also showed how to create a SAS/IML module that hides the details and enables you
As you develop a program in the SAS/IML language, it is often useful to create graphs to visualize intermediate results. The language supports basic statistical graphics such as bar charts, histograms, scatter plots, and so on. However, you can create more advanced graphics without leaving PROC IML by using the
A colleague asked me an interesting question: I have a journal article that includes sample quantiles for a variable. Given a new data value, I want to approximate its quantile. I also want to simulate data from the distribution of the published data. Is that possible? This situation is common.
A colleague sent me an interesting question: What is the best way to abort a SAS/IML program? For example, you might want to abort a program if the data is singular or does not contain a sufficient number of observations or variables. As a first attempt would be to try
My last blog post described three ways to add a smoothing spline to a scatter plot in SAS. I ended the post with a cautionary note: From a statistical point of view, the smoothing spline is less than ideal because the smoothing parameter must be chosen manually by the user.
In 2013 I published 110 blog posts. Some of these articles were more popular than others, often because they were linked to from a SAS newsletter such as the SAS Statistics and Operations Research News. In no particular order, here are some of my most popular posts from 2013, organized
The mosaic plot is a graphical visualization of a frequency table. In a previous post, I showed how to use the FREQ procedure to create a mosaic plot. This article shows how to create a mosaic plot by using the MOSAICPARM statement in the graph template language (GTL). (The MOSAICPARM
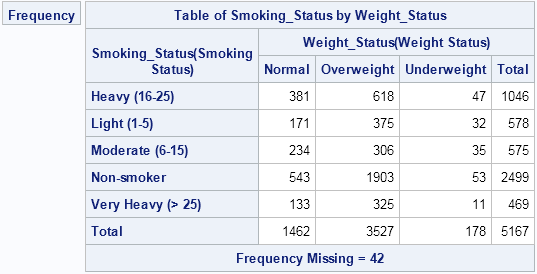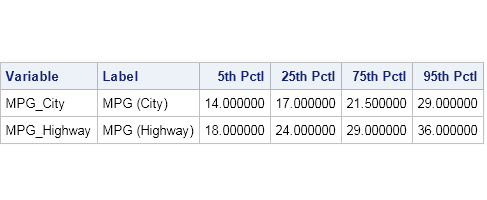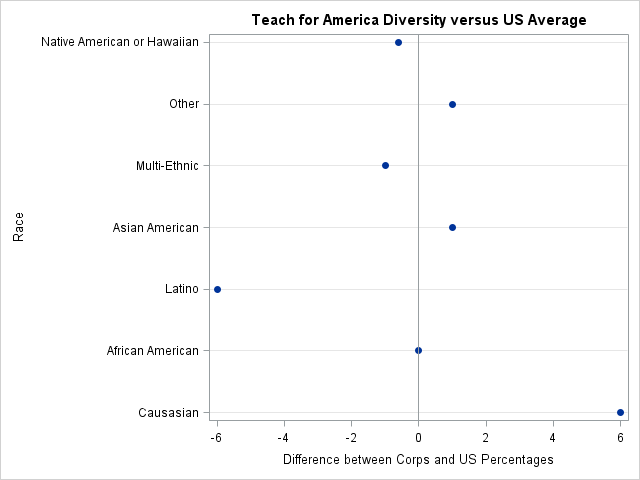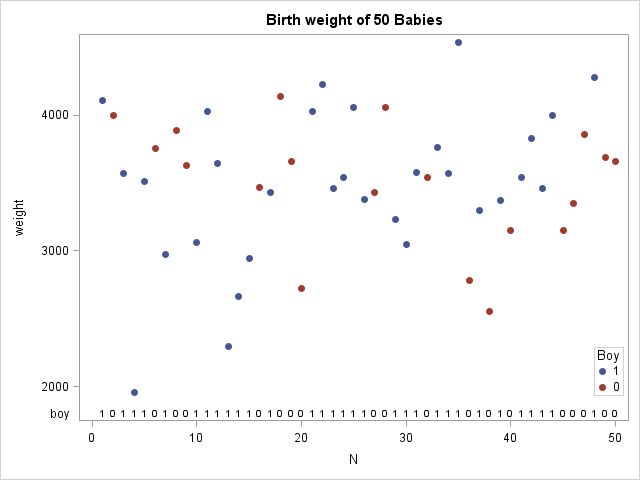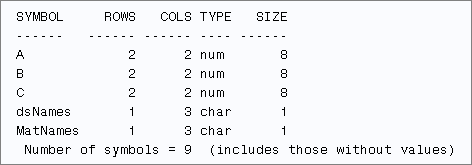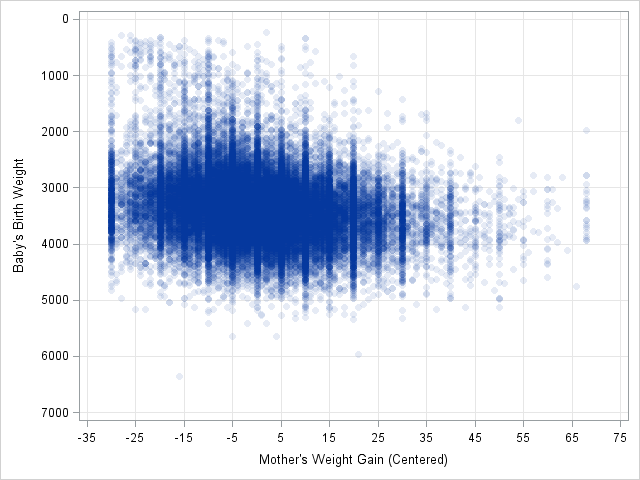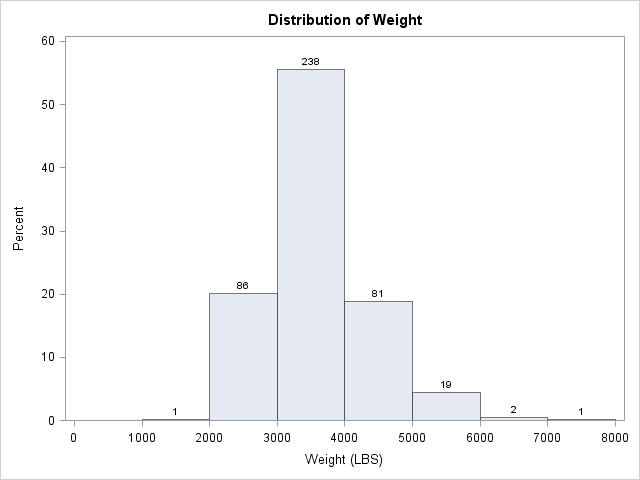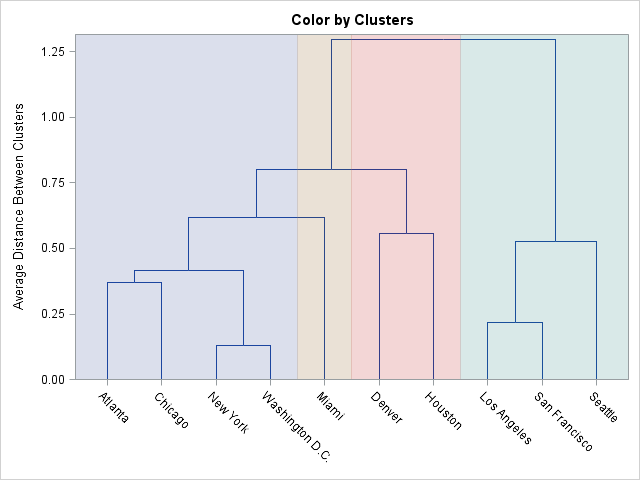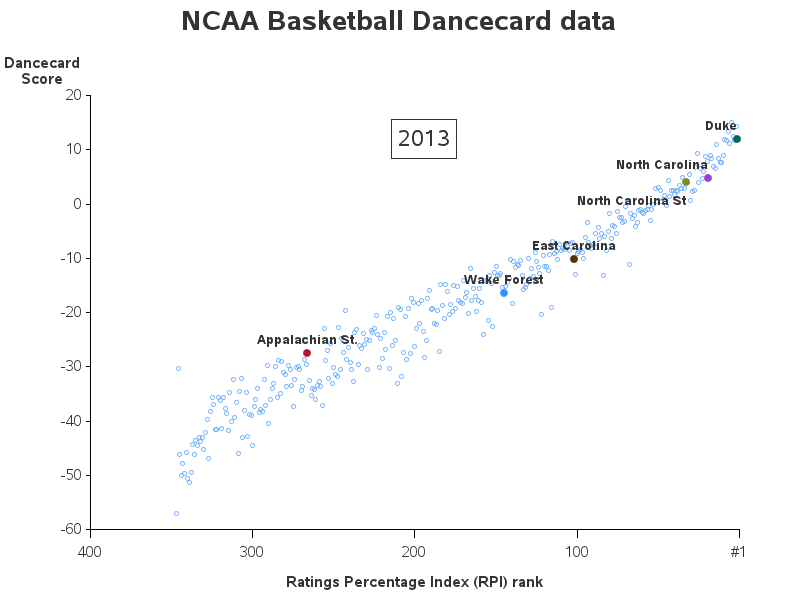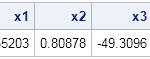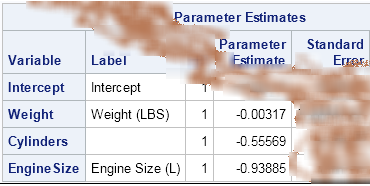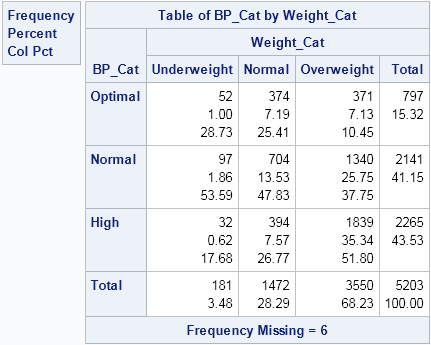
Mosaic plots (Hartigan and Kleiner, 1981; Friendly, 1994, JASA) are used for exploratory data analysis of categorical data. Mosaic plots have been available for decades in SAS products such as JMP, SAS/INSIGHT, and SAS/IML Studio. However, not all SAS customers have access to these specialized products, so I am pleased
If you've ever tried to use PROC FREQ to create a frequency table of two character variables, you know that by default the categories for each variable are displayed in alphabetical order. A different order is sometimes more useful. For example, consider the following two-way table for the smoking status
A challenge for statistical programmers is getting data into the right form for analysis. For graphing or analyzing data, sometimes the "wide format" (each subject is represented by one row and many variables) is required, but other times the "long format" (observations for each subject span multiple rows) is more
On Kaiser Fung's Junk Charts blog, he showed a bar chart that was "published by Teach for America, touting its diversity." Kaiser objected to the chart because the bar lengths did not accurately depict the proportions of the Teach for America corps members. The chart bothers me for another reason:
In my last blog post I described how to implement a "runs test" in the SAS/IML language. The runs test determines whether a sequence of two values (for example, heads and tails) is likely to have been generated by random chance. This article describes two applications of the runs test.
While walking in the woods, a statistician named Goldilocks wanders into a cottage and discovers three bears. The bears, being hungry, threaten to eat the young lady, but Goldilocks begs them to give her a chance to win her freedom. The bears agree. While Mama Bear and Papa Bear block
"It's a floor wax, and a dessert topping" - this pretty much describes SAS/Graph! (bonus points if you know where this quote came from!) Some people think of SAS as just a quality control tool. Others think of it as just a sales & marketing tool. And yet others think
SAS 9 has supported calling R from the SAS/IML language since 2009. The interface to R is part of the SAS/IML language. However, there have been so many versions of SAS and R since 2009, that it is hard to remember which SAS release supports which versions of R. The
A common visualization is to compare characteristics of two groups. This article emphasizes two tips that will help make the comparison clear. First, consider graphing the differences between the groups. Second, in any plot that has a categorical axis, sort the categories by a meaningful quantity. This article is motivated
Earlier this week I posted a "guest blog" in which my 8th grade son described a visualization of data for the 2013 ASA Poster Competition. The purpose of today's blog post is to present a higher-level statistical analysis of the same data. I will use a t test and a
Editor's Note: My 8th grade son, David, created a poster that he submitted to the 2013 ASA Poster Competition. The competition encourages students to display "two or more related graphics that summarize a set of data, look at the data from different points of view, and answer specific questions about
Do you have dozens (or even hundreds) of SAS data sets that you want to read into SAS/IML matrices? In a previous blog post, I showed how to iterate over a series of data sets and analyze each one. Inside the loop, I read each data set into a matrix
In a previous article I discussed how to bin univariate observations by using the BIN function, which was added to the SAS/IML language in SAS/IML 9.3. You can generalize that example and bin bivariate or multivariate data. Over two years ago I wrote a blog post on 2D binning in
It is often useful to partition observations for a continuous variable into a small number of intervals, called bins. This familiar process occurs every time that you create a histogram, such as the one on the left. In SAS you can create this histogram by calling the UNIVARIATE procedure. Optionally,
