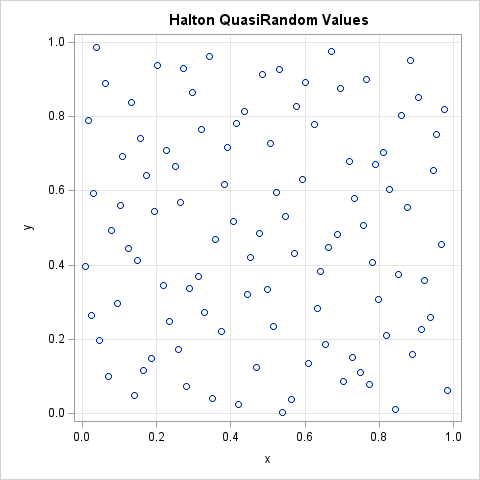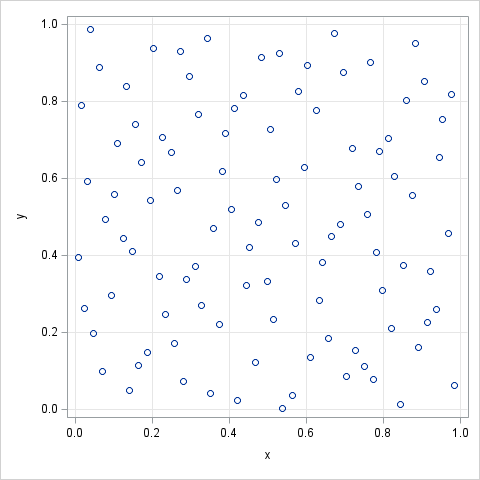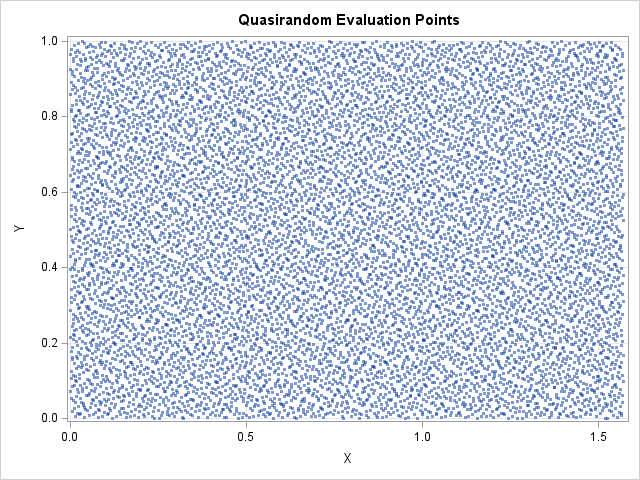
It is difficult to evaluate high-dimensional integrals. One numerical technique that can be useful is quasi-Monte Carlo integration. In this article, I show how you can generate quasirandom points in SAS and use them to evaluate a definite integral on a compact region. For simplicity, the example in this article