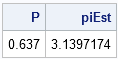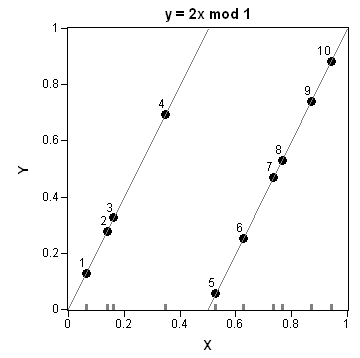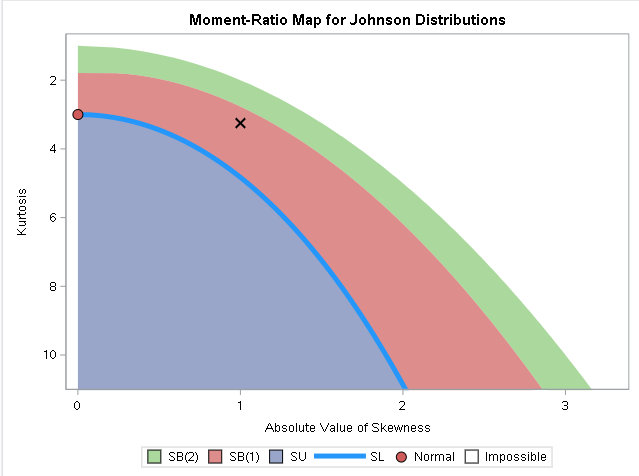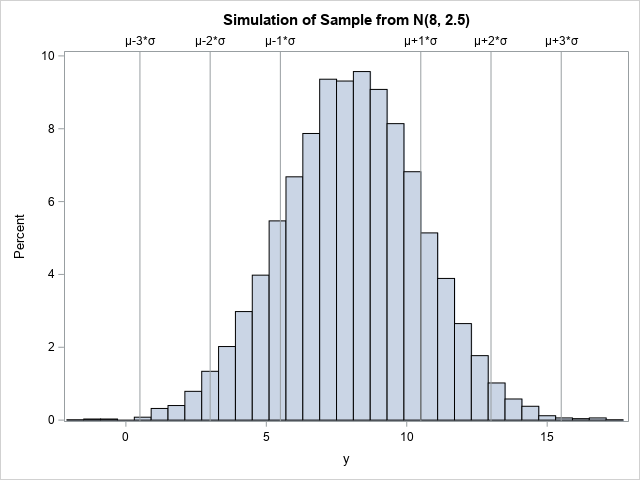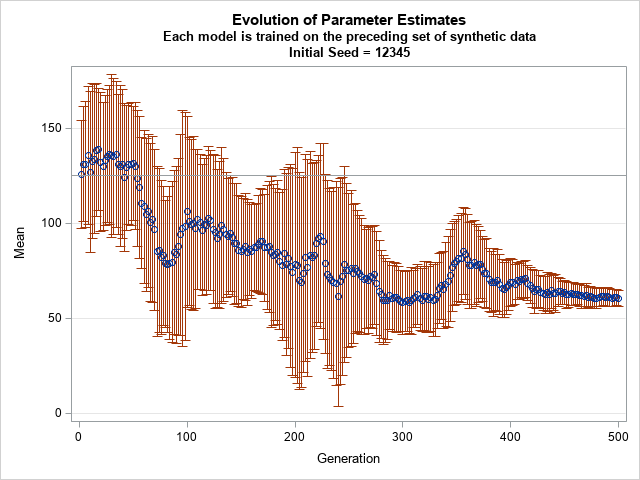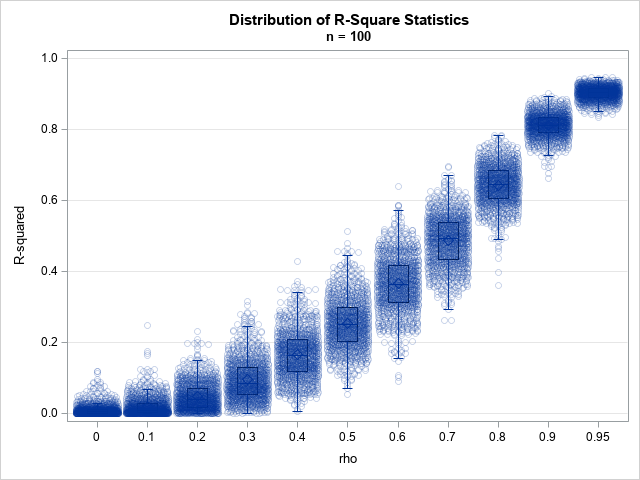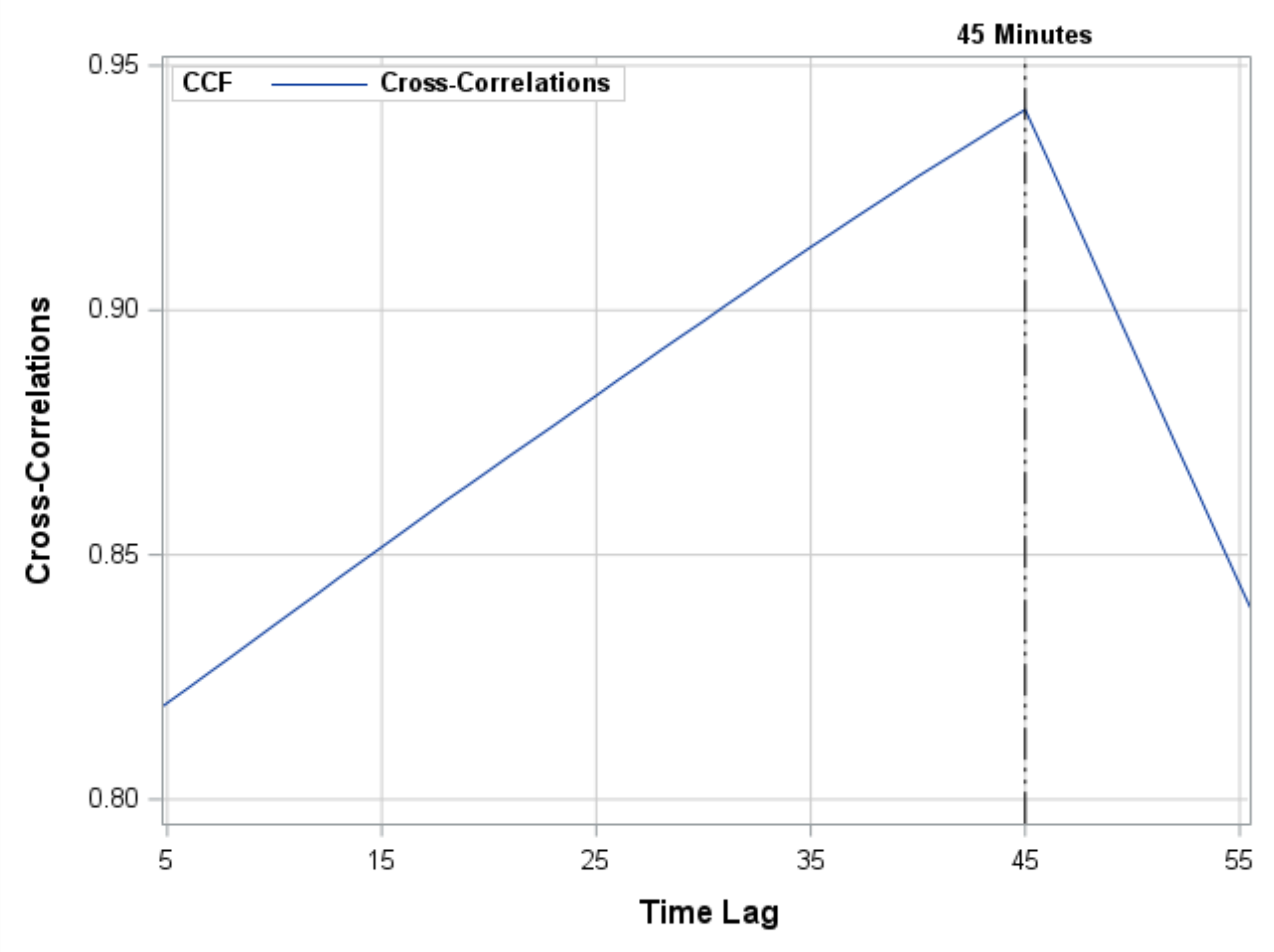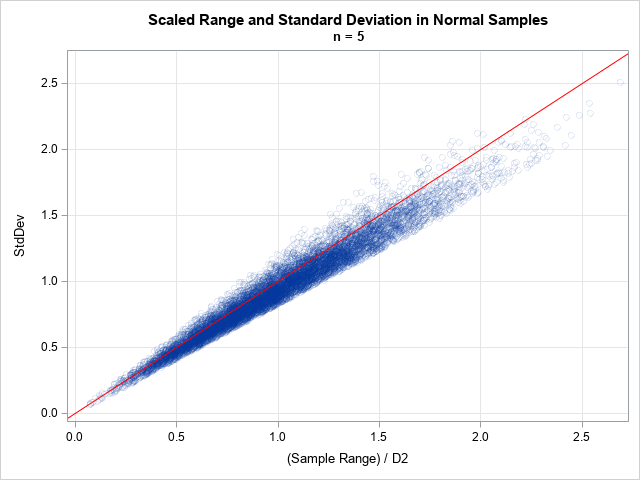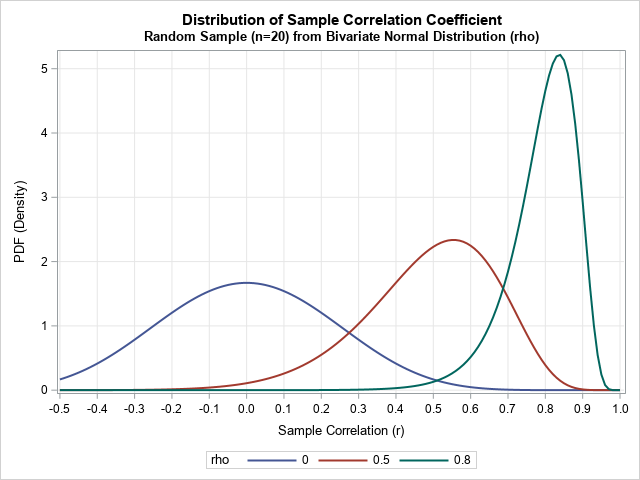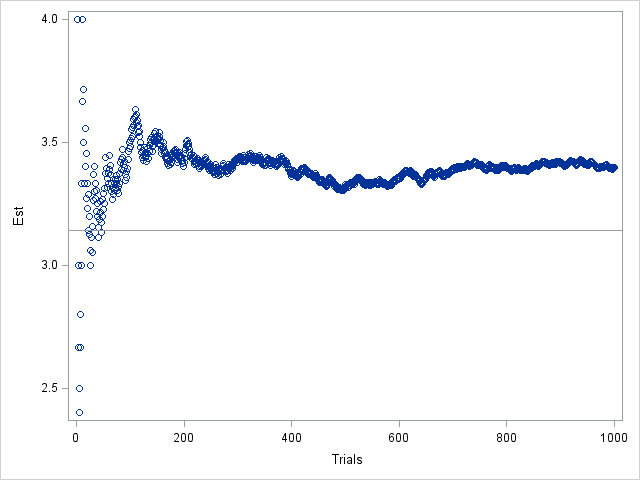
In my article on Buffon's needle experiment, I showed a graph that converges fairly nicely and regularly to the value π, which is the value that the simulation is trying to estimate. This graph is, indeed, a typical graph, as you can verify by running the simulation yourself. However, notice
Buffon's needle experiment for estimating π is a classical example of using an experiment (or a simulation) to estimate a probability. This example is presented in many books on statistical simulation and is famous enough that Brian Ripley in his book Stochastic Simulation states that the problem is "well known
Last week I presented the GSR algorithm, a statistical model of a riffle shuffle. In the model, a deck of n cards is split into two parts according to the binomial distribution. Each piece has roughly n/2 cards. Then cards are dropped from the two stacks according to the number
If you haven't signed up for SAS Global Forum 2011 in Las Vegas, you'd better get moving: February 28 is the last day for early registration and the discounted hotel prices. You should also sign up for the pre-conference statistical tutorials, which are filling up fast! I was tempted to
Digital twins are revolutionizing manufacturing by providing real-time, virtual representations of physical assets. The ability to create and refine digital replicas using live sensor data is optimizing efficiency, reducing downtime and unlocking new levels of innovation. While many organizations are still operating with “digital shadows” – historical data models that
Navigating the interpretability paradox of autonomous AI: Can we maintain trust and transparency without sacrificing performance? AI has rapidly evolved from simple, rule-based systems into sophisticated autonomous agents capable of making decisions without direct human oversight. These advanced systems, known as "agentic AI," go beyond basic automation to independently sense
SAS/STAT offers a principled treatment of missing data in a frequentist paradigm. SAS' Michael Senter reveals how with a few code tweaks, you can seamlessly transition to a Bayesian analysis.
Once a bastion of stability, the banking industry now finds itself navigating a complex world of evolving risks. From economic uncertainty and geopolitical tensions to AI advancements and climate crises, the industry is navigating a whirlwind of risks that show no signs of slowing down. What worked in the past
In a previous article, I presented some of the most popular blog posts from The DO Loop in 2024. In general, popular articles deal with elementary topics that have broad appeal. However, I also write technical articles about advanced topics, which typically do not make it onto a Top 10
What does the path to a fully AI-integrated government look like? “Figure out where you want to be and then take the steps to get there.” I remember my dad giving me that advice when I was growing up, and I think about it now as I watch the unfolding
SAS' Danny Sprukulis walks through how he developed a model theme park to simulate attraction wait times for operational decision-making.
A previous article discusses how to generate a random covariance matrix with a specified set of (positive) eigenvalues. A SAS programmer asked whether it is possible to produce a correlation matrix that has a specified set of eigenvalues. After discussing the problem with a friend, I am happy to report
Fairness, transparency, integrity and competition are essential for managing public funds. We rely on departments to choose the best value from the private sector. Efficient public procurement improves services, infrastructure, and the economy. It must also be accountable to the public by protecting financial loss from fraud, waste, abuse, and
When the SAS Global Forum 2020 conference was cancelled by the global COVID-19 pandemic, I felt sorry for the customers and colleagues who had spent months preparing their presentations. One presentation I especially wanted to attend was by Bucky Ransdell and Randy Tobias: "Introducing PROC SIMSYSTEM for Systematic Nonnormal Simulation".
Data science continues to be a pivotal force driving innovation across industries. From enhancing customer experiences to optimizing operational efficiencies, the role of data science is expanding, bringing with it new challenges and opportunities. This article explores the emerging trends and technologies that are shaping the future of data science
A remarkable result in probability theory is the "three-sigma rule," which is a generic name for theorems that bound the probability that a univariate random variable will appear near the center of its distribution. This article discusses the familiar three-sigma rule for the normal distribution, a less-familiar rule for unimodal
This article shows how to simulate data from a Poisson regression model, including how to account for an offset variable. If you are not familiar with how to run a Poisson regression in SAS, see the article "Poisson regression in SAS." A Poisson regression model is a specific type of
An article published in Nature has the intriguing title, "AI models collapse when trained on recursively generated data." (Shumailov, et al., 2024). The article is quite readable, but I also recommend a less technical overview of the result: "AI models fed AI-generated data quickly spew nonsense" (Gibney, 2024). The Gibney
A SAS analyst ran a linear regression model and obtained an R-square statistic for the fit. However, he wanted a confidence interval, so he posted a question to a discussion forum asking how to obtain a confidence interval for the R-square parameter. Someone suggested a formula from a textbook (Cohen,
Batch manufacturing involves producing goods in batches rather than in a continuous stream. This approach is common in industries such as pharmaceuticals, chemicals, and materials processing, where precise control over the production process is essential to ensure product quality and consistency. One critical aspect of batch manufacturing is the need to manage and understand inherent time delays that occur at various stages of the process.
A SAS statistical programmer recently asked a theoretical question about statistics. "I've read that 'p-values are uniformly distributed under the null hypothesis,'" he began, "but what does that mean in practice? Is it important?" I think data simulation is a great way to discuss the conditions for which p-values are
In a recent article, I graphed the PDF of a few Beta distributions that had a variety of skewness and kurtosis values. I thought that I had chosen the parameter values to represent a wide variety of Beta shapes. However, I was surprised to see that the distributions were all
The moment-ratio diagram is a tool that is useful when choosing a distribution that models a sample of univariate data. As I show in my book (Simulating Data with SAS, Wicklin, 2013), you first plot the skewness and kurtosis of the sample on the moment-ratio diagram to see what common
A SAS programmer wanted to simulate samples from a family of Beta(a,b) distributions for a simulation study. (Recall that a Beta random variable is bounded with values in the range [0,1].) She wanted to choose the parameters such that the skewness and kurtosis of the distributions varied over range of
Imagine a not-so-distant future where quantum computing reshapes our approach to solving some of businesses’ and society’s most pressing issues. This isn’t fantasy. Just as nuclear energy, 3D printing and gene therapy transitioned from science fiction to scientific reality, quantum computing is on the brink of becoming the next transformative
As the old saying goes, “You wait ages for a bus and then two [or possibly three]come along at once.” This saying can be updated to reflect life in our increasingly digital world: "You wait ages for a genuine disruptive technology and then two [or possibly three]arrive simultaneously." This phrase
Careers in risk management can be rewarding. The disciplines are key to a broad range of industries. Risk management teases the analytical side of the brain and there is a clear line of contribution between the work and the organization's performance. Careers in risk management are also shrouded in mystery
Rare diseases, often called orphan diseases, affect a small percentage of the population. Despite their rarity, these diseases collectively impact millions worldwide. Being a health care professional who cares deeply about overall patient care, the challenges in diagnosing and treating rare diseases resonate profoundly with me. Limited data availability, dispersed
In statistical quality control, practitioners often estimate the variability of products that are being produced in a manufacturing plant. It is important to estimate the variability as soon as possible, which means trying to obtain an estimate from a small sample. Samples of size five or less are not uncommon
I read a journal article in which a researcher used a formula for the probability density function (PDF) of the sample correlation coefficient. The formula was rather complicated, and presented with no citation, so I was curious to learn more. I found the distribution for the correlation coefficient in the
