An article published in Nature has the intriguing title, "AI models collapse when trained on recursively generated data." (Shumailov, et al., 2024). The article is quite readable, but I also recommend a less technical overview of the result: "AI models fed AI-generated data quickly spew nonsense" (Gibney, 2024). The Gibney article includes a wonderful sequence of images that shows the effect on a generative AI when it is iteratively trained on its own output for several generations.

This blog post discusses the concept of "model collapse" and illustrates it by using a simple example: fitting a normal distribution to data.

Model collapse: meaning and causes

Today's large language models (LLMs) have been trained on human-created content. However, as more and more people (and magazines and newspapers) use AI to generate articles and web pages, future generations of LLMs will be trained on some content that was generated by previous generations of AI models. The Shumailov et al (2024) article discusses generative AI models and explores an intriguing question: What might be the effect on future AI models if they are trained on the input of previous generative AI models?

In short, this kind of "inbreeding" can cause future AI to generate less diverse output. The reason is that a LLM tends to over-predict events that have high probability and under-predict rare events. Consequently, if this process repeats itself over several generations of AI models, the models of the future will increasingly generate high-probability events and rarely generate low-probability events. This kind of model evolution is known as "model collapse."

To quote Shumailov et al (2024), "Model collapse is a degenerative process ... in which the data [that the models] generate end up polluting the training set of the next generation. Being trained on polluted data, they then mis-perceive reality. ... The model begins losing information about the tails of the distribution, [and eventually] converges to a distribution that carries little resemblance to the original one, often with substantially reduced variance."

Is this something that users of today's generative AI should worry about? Probably not, but it is important for individuals and companies that are training AI models. As newspapers, magazines, and websites begin to publish AI-generated content, we all must be aware of the potential impact that AI-generated content has on future generations of AI models.

A simple statistical example

It's not difficult to come up with a simplified model that illustrates the concepts in the paper. You don't need to use complex LLM models with millions of parameters. In fact, the basic concepts can be illustrated by using univariate data and familiar probability distributions. This section illustrates model drift and collapse by using a toy example.

Suppose you have some data, X⁰ = {x⁰_i | i=1..n}, and you decide to model it by using a normal distribution. You fit the model to the data and obtain estimates for the mean (m₀) and standard deviation (s₀) so that the model is N(m₀, s₀). Now, generate synthetic data X¹ = {x¹_i | i=1..n} as a sample of size n that is distributed as N(m₀, s₀).

So far, these are the standard steps for a simulation study. But suppose you decide to build a new model, and you fit the model by using only the synthetic data instead of the real data. You are now building a model of the model, rather than a model of reality! The new model contains the parameters m₁ and s₁, which are computed from the synthetic data.

Obviously, you can continue this process. At each generation, create new synthetic data X^k+1 based on the model built from the synthetic data from the previous generation, which is N(m_k, s_k).

This is a random process, but the following graph shows one possible evolution of the parameters (m_i, s_i) for 500 generations of this process:

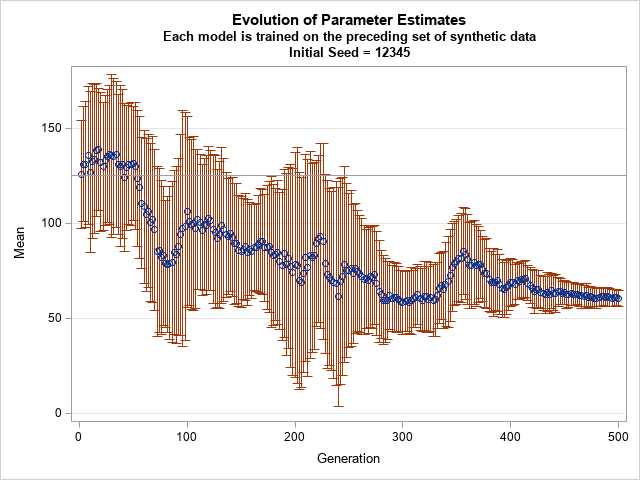
In the graph, a blue dot is placed at the mean of the distribution. Reddish bars indicate the standard deviation. The original data had a mean equal to 125 and a standard deviation of 30. After many generations, the mean drifts away from its original value and the standard deviation decreases. After 500 generations, the mean is less than half its original value, and the standard deviation has shrunk to about 4. The smaller standard deviation implies that the model for the 500th generation is much less diverse that the original data. Synthetic data generated by this 500th model is quite different from the original data.

Does the process always evolve in this way? No. The parameters evolve as part of a random process. If you use a different set of random number seeds, the evolution will be different. At each generation, the standard deviation can grow or shrink, but Shumailov et al (2024) claim that the standard deviation will probably shrink after many generations. I haven't read their proof, but here's another run for the normal model. The initial model is the same as before, but the evolution uses a different set of random numbers to generate the synthetic data at each step of the fit-generate-fit sequence:

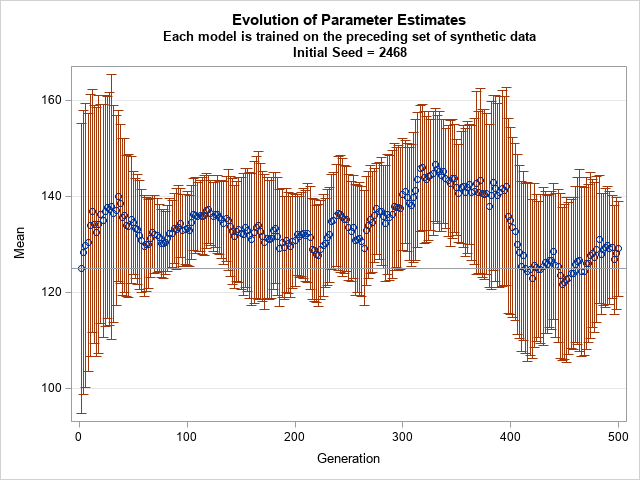
In this new graph, the mean of the sample has not drifted very much. The standard deviation shrinks dramatically after about 100 generations but increases slightly in later generations. After 500 generations, the standard deviation is about 10, as compared to the initial value of 30.

SAS programmers can download and run the SAS program that I used to generate these graphs. Feel free to run your own experiments to get an intuitive feel for the range of possible evolutions of the parameters.

Too simple?

The normal model has a very nice statistical property: the estimation process is unbiased. This is not always the case for more complex models. For example, the usual sample estimates for skewness and kurtosis are biased, so any parameter estimates that use high-order moments will be biased as well.

For fun, I performed some additional simulations with the three-parameter lognormal family of distributions. My experiments indicate that some parameters can change rapidly from generation to generation. For example, the estimate of the threshold parameter in a lognormal model is much more sensitive to the fit-simulate-fit process than for the log-location or log-scale parameters. The important fact is that it might take only a few generations before the model distribution no longer looks like the original data. The program for the three-parameter lognormal family is also available for download.

Summary

The Shumailov et al (2024) article discusses generative AI models and what might happen if you train a large language model on content that was itself generated from an LLM. They performed an experiment that shows if you train an AI model by using only synthetic data generated from a previous generative AI model, you can get model collapse after a small number of generations. Although LLMs have millions of parameters, you can observe similar behavior in toy examples such as simulation from a normal or lognormal distribution. Hopefully, these overly simple examples give some perspective into model collapse, and why researchers worry about it.

In practice, future AI models are likely to be trained on a combination of real and synthetic data. "When Shumailov and his team fine-tuned each model on 10% real data, alongside synthetic data, collapse occurred more slowly." (Gibney, 2024)

This blog post reminds us that synthetic data is, by definition, generated from a model. When you use synthetic data to build a model, you a building a model of a model. There are times when this is useful. However, a model built from real data is usually more diverse in its predictions because real data tends to be messier than synthetic data.