Last week I presented the GSR algorithm, a statistical model of a riffle shuffle. In the model, a deck of n cards is split into two parts according to the binomial distribution. Each piece has roughly n/2 cards. Then cards are dropped from the two stacks according to the number of cards remaining in each stack. I lamented at the end of the post that the algorithm is not easily vectorized because the probabilities of cards falling from the left and right stack change during the riffle.
An Equivalent Model
The GSR model has an equivalent geometric formulation (see "Bayer and Diaconis (1992)", p. 299), as follows:
- Generate n random points from the uniform distribution on [0,1] and label them in order x1 < x2 < ... < xn.
- Transform these points under the mapping y = 2x mod 1.
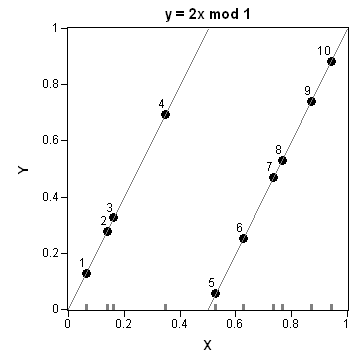
The mapping transforms the points by breaking them into two groups. Points less than 0.5 are stretched out and mapped into [0,1]. Points greater than 0.5 are also stretched out and mapped into [0,1]. Thus the mapping does two things: it separates the points into two groups (a left group and a right group) and it interleaves the two groups.
Bayer and Diaconis prove that this simple geometric transformation is equivalent to the GSR model and therefore describes a riffle shuffle. For example, the image on this page shows ten points in [0,1]. The initial X-axis ordering (1, 2, .., 10) is mapped into a new ordering on the Y axis. The shuffled order is 5, 1, 6, 2, 3, 7, 8, 4, 9, 10.
The Geometric GSR Algorithm
This algorithm is easily implemented as a SAS/IML function. The RANDGEN subroutine is used to generate random numbers from the uniform distribution. The SORT and SORTNDX subroutines are used sort the points and to rearrange the cards in the deck according to the "2x mod 1" transformation. (See a previous blog post for more information on sorting.)
The following SAS/IML module implements the geometric algorithm:
proc iml;
/** Gilbert-Shannon-Reeds statistical model
of a riffle shuffle (geometric version). **/
start RiffleShuffle(deck);
n = nrow(deck);
x = j(n,1);
call randgen(x, "Uniform");
call sort(x, 1);
/** cut into two stacks by binomial distribution **/
y = mod(2 * x, 1);
call sortndx(idx, y, 1);
return(deck[idx]);
finish; |
You can test the algorithm by starting with a deck of cards in a known order and observing how the cards are mixed by consecutive riffle shuffles. The following statements riffle the cards seven times and store the results of each shuffle. To save space, a 20-card deck is used. The original order of the cards is denoted 1, 2, 3, ..., 20.
call randseed(1234); n = 20; deck = T(1:n); s = j(n, 8); s[,1] = deck; do i = 1 to 7; s[,i+1] = RiffleShuffle( s[,i] ); end; names = "s0":"s7"; print s[colname=names]; |
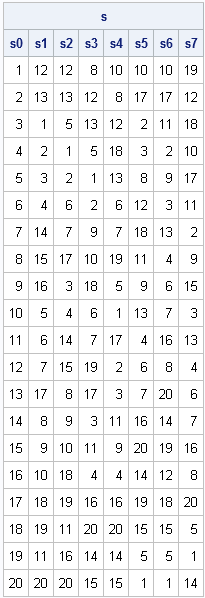
Timing the performance of the two GSR algorithms indicates that the geometric RiffleShuffle algorithm is about six times faster than the original implementation. Consequently, if you intend to simulate how cards are mixed during shuffling, use this algorithm instead of the initial straightforward implementation of the GSR model.
References
- D. Bayer and P. Diaconis (1992), "Trailing the Dovetail Shuffle to Its Lair," Annals of Applied Probablity 2(2) 294-313

2 Comments
I never would have guessed that you could "shuffle" cards with a simple piecewise function!
Pingback: Readers’ choice 2011: The DO Loop’s 10 most popular posts - The DO Loop