
When I was at SAS Global Forum last week, a SAS user asked my advice regarding a SAS/IML program that he wrote. One step of the program was taking too long to run and he wondered if I could suggest a way to speed it up. The long-running step was

When I was at SAS Global Forum last week, a SAS user asked my advice regarding a SAS/IML program that he wrote. One step of the program was taking too long to run and he wondered if I could suggest a way to speed it up. The long-running step was
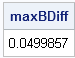
In statistical programming, I often test a program by running it on a problem for which I know the correct answer. I often use a single expression to compute the maximum value of the absolute difference between the vectors: maxDiff = max( abs( z-correct ) ); /* largest absolute difference
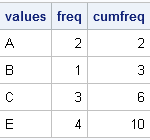
A reader asked: I want to create a vector as follows. Suppose there are two given vectors x=[A B C] and f=[1 2 3]. Here f indicates the frequency vector. I hope to generate a vector c=[A B B C C C]. I am trying to use the REPEAT function
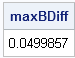
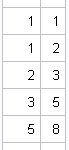
To a statistician, the DIF function (which was introduced in SAS/IML 9.22) is useful for time series analysis. To a numerical analyst and a statistical programmer, the function has many other uses, including computing finite differences. The DIF function computes the difference between the original vector and a shifted version
To a statistician, the LAG function (which was introduced in SAS/IML 9.22) is useful for time series analysis. To a numerical analyst and a statistical programmer, the function provides a convenient way to compute quantitites that involve adjacent values in any vector. The LAG function is essentially a "shift operator."

I blog about a lot of topics, but the following five categories represent some of my favorite subjects. Judging by the number of readers and comments, these articles have struck a chord with SAS users. If you haven't read them, check them out. (If you HAVE read them, some are
SAS software provides many run-time functions that you can call from your SAS/IML or DATA step programs. The SAS/IML language has several hundred built-in statistical functions, and Base SAS software contains hundreds more. However, it is common for statistical programmers to extend the run-time library to include special user-defined functions.
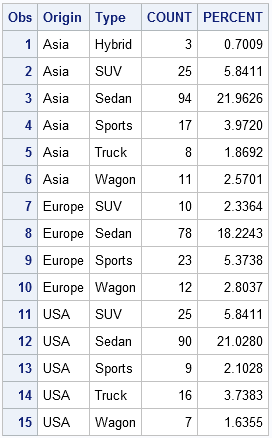
Because the SAS/IML language is a general purpose programming language, it doesn't have a BY statement like most other SAS procedures (such as PROC REG). However, there are several ways to loop over categorical variables and perform an analysis on the observations in each category. One way is to use
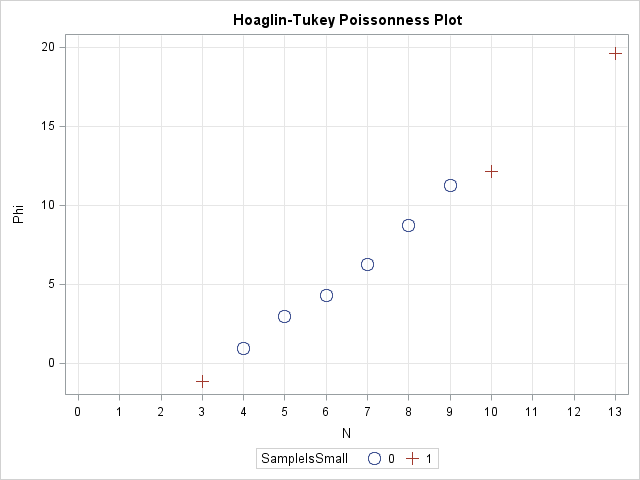
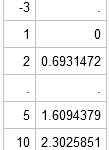
Last week I discussed how to fit a Poisson distribution to data. The technique, which involves using the GENMOD procedure, produces a table of some goodness-of-fit statistics, but I find it useful to also produce a graph that indicates the goodness of fit. For continuous distributions, the quantile-quantile (Q-Q) plot
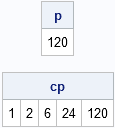
The birthday matching problem is a classic problem in probability theory. The part of it that people tend to remember is that in a room of 23 people, there is greater than 50% chance that two people in the room share a birthday. But the birthday matching problem is also
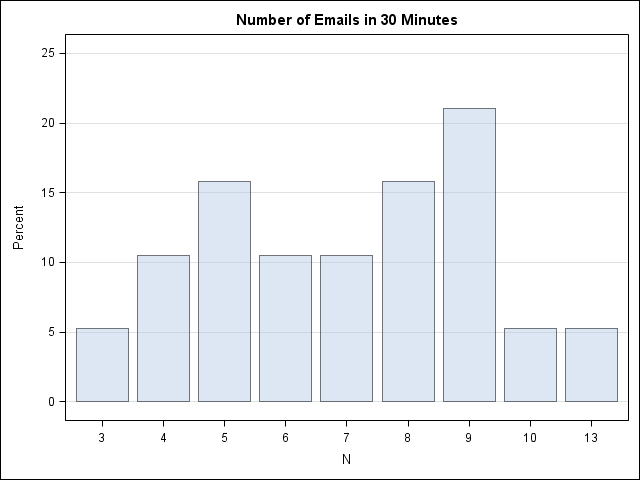
Over at the SAS Discussion Forums, someone asked how to use SAS to fit a Poisson distribution to data. The questioner asked how to fit the distribution but also how to overlay the fitted density on the data and to create a quantile-quantile (Q-Q) plot. The questioner mentioned that the
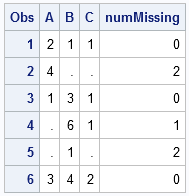
Locating missing values is important in statistical data analysis. I've previously written about how to count the number of missing values for each variable in a data set. In Base SAS, I showed how to use the MEANS or FREQ procedures to count missing values. In the SAS/IML language, I
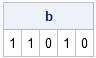
The fundamental units in the SAS/IML language are matrices and vectors. Consequently, you might wonder about conditional expression such as if v>0 then.... What does this expression mean when v contains more than a single element? Evaluating vector expressions When you test a vector for some condition, expressions like v>0
Covariance, correlation, and distance matrices are a few examples of symmetric matrices that are frequently encountered in statistics. When you create a symmetric matrix, you only need to specify the lower triangular portion of the matrix. The VECH and SQRVECH functions, which were introduced in SAS/IML 9.3, are two functions

The SAS/IML language supports both row vectors and column vectors. This is useful for performing linear algebra, but it can cause headaches when you are writing a SAS/IML module. I want my modules to be able to handle both row vectors and column vectors. I don't want the user to
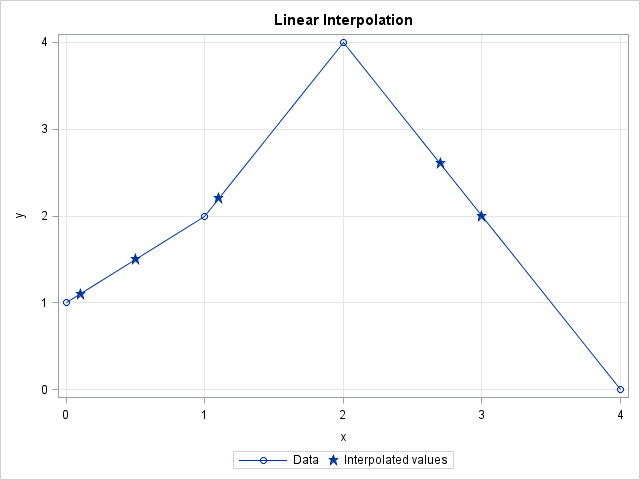
A recent discussion on the SAS-L discussion forum concerned how to implement linear interpolation in SAS. Some people suggested using PROC EXPAND in SAS/ETS software, whereas others proposed a DATA step solution. For me, the SAS/IML language provides a natural programming environment to implement an interpolation scheme. It also provides
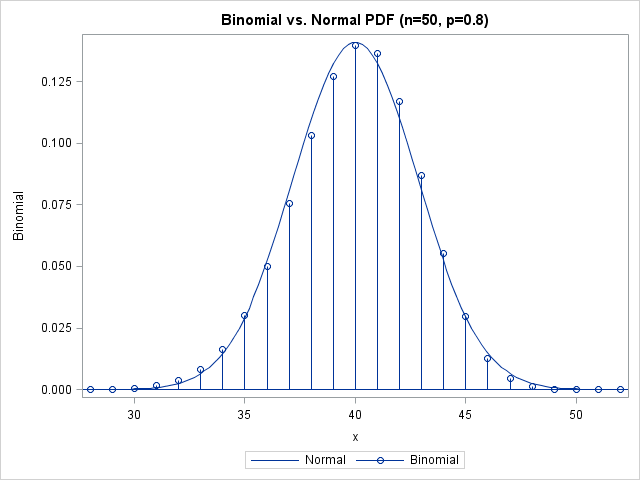
Most statistical programmers have seen a graph of a normal distribution that approximates a binomial distribution. The figure is often accompanied by a statement that gives guidelines for when the approximation is valid. For example, if the binomial distribution describes an experiment with n trials and the probability of success
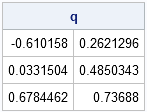
SAS provides several ways to compute sample quantiles of data. The UNIVARIATE procedure can compute quantiles (also called percentiles), but you can also compute them in the SAS/IML language. Prior to SAS/IML 9.22 (released in 2010) statistical programmers could call a SAS/IML module that computes sample quantiles. With the release
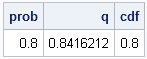
I work with continuous distributions more often than with discrete distributions. Consequently, I am used to thinking of the quantile function as being an inverse cumulative distribution function (CDF). (These functions are described in my article, "Four essential functions for statistical programmers.") For discrete distributions, they are not. To quote
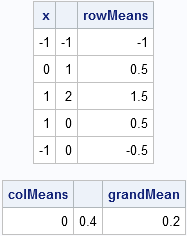
As a SAS developer, I am always looking ahead to the next release of SAS. However, many SAS customer sites migrate to new releases slowly and are just now adopting versions of SAS that were released in 2010 or 2011. Consequently, I want to write a few articles that discuss
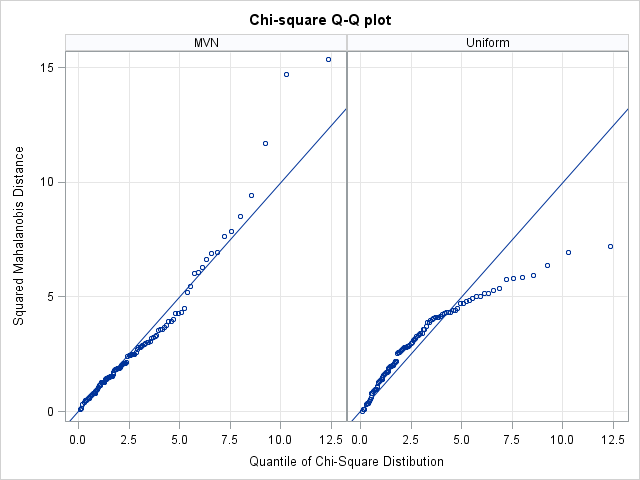
I've blogged several times about multivariate normality, including how to generate random values from a multivariate normal distribution. But given a set of multivariate data, how can you determine if it is likely to have come from a multivariate normal distribution? The answer, of course, is to run a goodness-of-fit

I recently saw a SAS Knowledge Base article called "How to stop processing your code if a certain condition is met." The article discusses the use of the %RETURN macro statement to abort the execution of a SAS program if some condition occurs. The "condition" is usually an error that
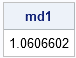
I recently blogged about Mahalanobis distance and what it means geometrically. I also previously showed how Mahalanobis distance can be used to compute outliers in multivariate data. But how do you compute Mahalanobis distance in SAS? Computing Mahalanobis distance with built-in SAS procedures and functions There are several ways to
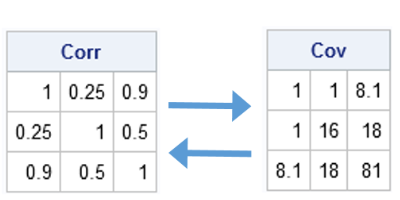
I have previously blogged about how to convert a covariance matrix into a correlation matrix in SAS (and the other way around). However, I still get questions about it, perhaps because my previous post demonstrated more than one way to accomplish each transformation. To eliminate all confusion, the following SAS/IML
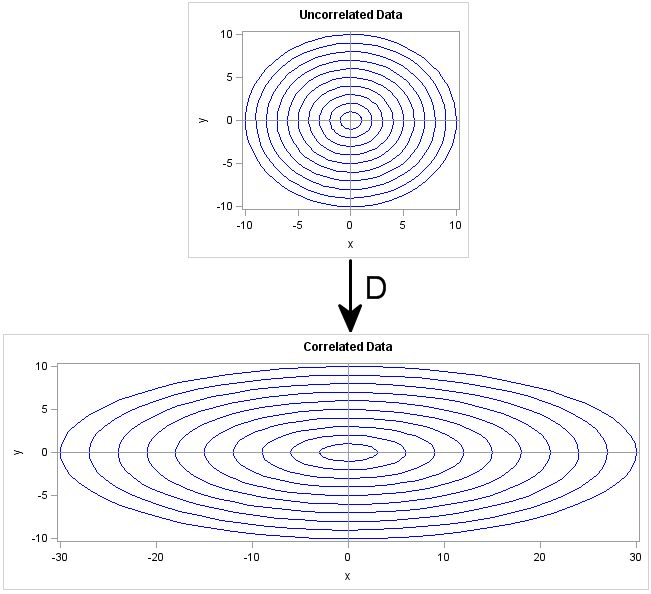
A variance-covariance matrix expresses linear relationships between variables. Given the covariances between variables, did you know that you can write down an invertible linear transformation that "uncorrelates" the variables? Conversely, you can transform a set of uncorrelated variables into variables with given covariances. The transformation that works this magic is
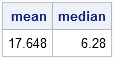
In two previous blog posts I worked through examples in the survey article, "Robust statistics for outlier detection," by Peter Rousseeuw and Mia Hubert. Robust estimates of location in a univariate setting are well-known, with the median statistic being the classical example. Robust estimates of scale are less well-known, with
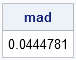
In a previous blog post on robust estimation of location, I worked through some of the examples in the survey article, "Robust statistics for outlier detection," by Peter Rousseeuw and Mia Hubert. I showed that SAS/IML software and PROC UNIVARIATE both support the robust estimators of location that are mentioned
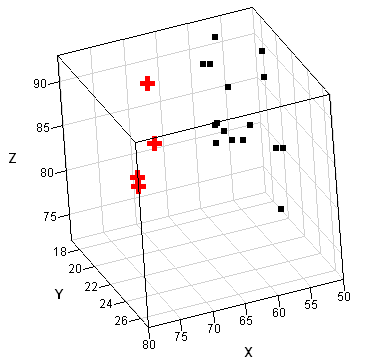
I encountered a wonderful survey article, "Robust statistics for outlier detection," by Peter Rousseeuw and Mia Hubert. Not only are the authors major contributors to the field of robust estimation, but the article is short and very readable. This blog post walks through the examples in the paper and shows
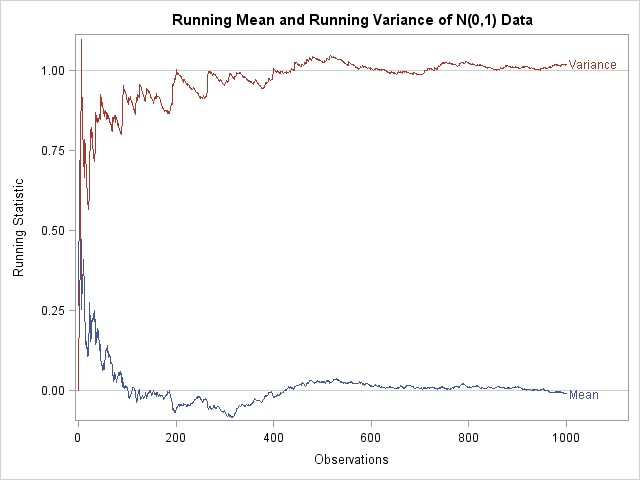
In my recent article on simulating Buffon's needle experiment, I computed the "running mean" of a series of values by using a single call to the CUSUM function in the SAS/IML language. For example, the following SAS/IML statements define a RunningMean function, generate 1,000 random normal values, and compute the
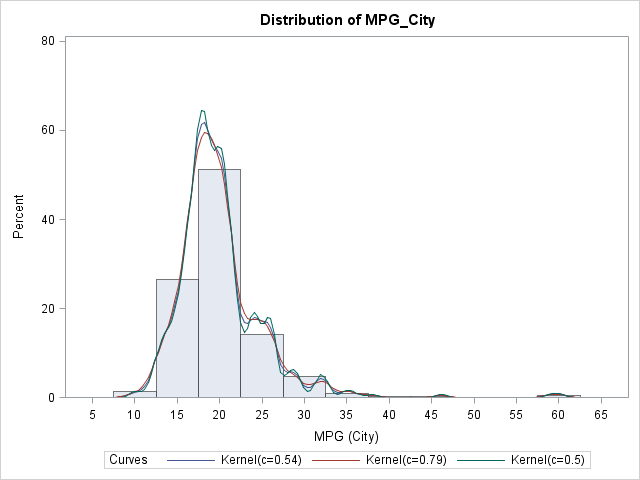
A recent question on a SAS Discussion Forum was "how can you overlay multiple kernel density estimates on a single plot?" There are three ways to do this, depending on your goals and objectives. Overlay different estimates of the same variable Sometimes you have a single variable and want to