I have previously blogged about how to convert a covariance matrix into a correlation matrix in SAS (and the other way around). However, I still get questions about it, perhaps because my previous post demonstrated more than one way to accomplish each transformation.
To eliminate all confusion, the following SAS/IML program implements a function that converts a covariance matrix into the associated correlation matrix. For an explanation of why this works, see my previous article.
proc iml;
/* convert a covariance matrix, S, to a correlation matrix */
start Cov2Corr(S);
D = sqrt(vecdiag(S));
return( S / D` / D ); /* divide columns, then divide rows */
finish;
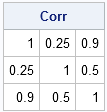
S = {1.0 1.0 8.1, /* test it */
1.0 16.0 18.0,
8.1 18.0 81.0 };
Corr = Cov2Corr(S);
print Corr; |
There are many covariance matrices that produce the same correlation matrix, therefore the inverse operation (which produces a covariance matrix from a correlation matrix) is not uniquely defined. However, if you specify the standard deviations for each variable, you can write a SAS/IML function that converts a correlation matrix to a covariance matrix:
/* R = correlation matrix
sd = (vector of) standard deviations for each variable
Return covariance matrix with sd##2 on the diagonal */
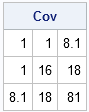
start Corr2Cov(R, sd);
std = colvec(sd);
return( std` # R #std );
finish;
/* convert correlation matrix to covariance matrix */
sd = {1 4 9}; /* std devs = sqrt(vecdiag(S)) */
Cov = Corr2Cov(Corr, sd);
print Cov; |
New in SAS/IML 12.3 software
Update: As of SAS/IML 12.3, these functions are now built into SAS/IML software. See the documentation for the CORR2COV function and the COV2CORR function.
Converting a covariance matrix to a correlation matrix with SAS/STAT software
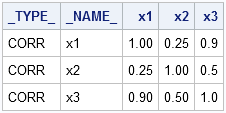
You can, of course, use the DATA step to convert a covariance matrix to a correlation matrix (and the other way around), but here's a neat trick that you can do in SAS/STAT software: the FACTOR procedure can read a covariance matrix (technically, a TYPE=COV data set) and write the corresponding correlation matrix to a SAS data set, as shown in the following example.
/* define covariance matrix as TYPE=COV data set (lower triangular) */ data cov(type=cov); _type_='COV'; input x1-x3; cards; 1 . . 1 16 . 8.1 18 81 ; run; /* convert covariance matrix to correlation matrix */ proc factor data=cov outstat=outstat noprint; run; proc print data=outstat noobs; where _TYPE_="CORR"; run; |
Does anyone know of a slick trick that converts a correlation matrix (and standard deviations) into a covariance matrix without using SAS/IML software? Post your solution in the comments.

6 Comments
Pingback: Computing the nearest correlation matrix - The DO Loop
Pingback: Overview of new features in SAS/IML 12.3 - The DO Loop
Love this blog!
I have a question about singular covariance matrices! I seem to have run into one...and my understanding is that this should not be the case. I am considering a 189x189 covariance matrix produced by a major ratings agency. I tried to use this covariance matrix to produce a correlation matrix, but the covariance matrix appears to be non-invertible, or singular, or have a determinant = 0.
Does your IML text or your simulation text address this scenario?
Thanks
Brian
Yes, this can happen. It occurs when a variable (column of a matrix) is a linear combination of the other variables (columns). For example:
x = shape(1:12, 4);
cov = cov(x);
d = det(cov);
print d;
The workaround is to identify the collinearities in the data. Alternatively, run PROC PRINCOMP or PROC VARCLUS on the data to obtain a lower dimensional set of variables that nevertheless captures most (or all) of the variance.
Pingback: A simple way to construct a large correlation matrix - The DO Loop
Pingback: Generate correlation matrices with specified eigenvalues - The DO Loop