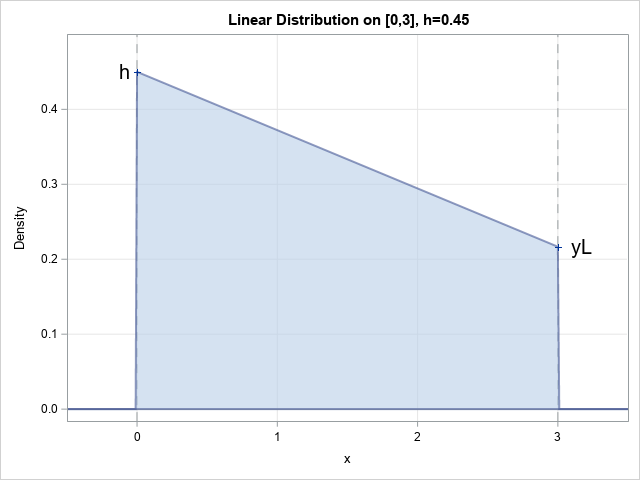
In a recent Monte Carlo project, I needed to simulate numbers on an interval by using a continuous linear probability density function (PDF). An example is shown to the right. In this example, the linear density function is decreasing on the interval, but the function could also be constant or