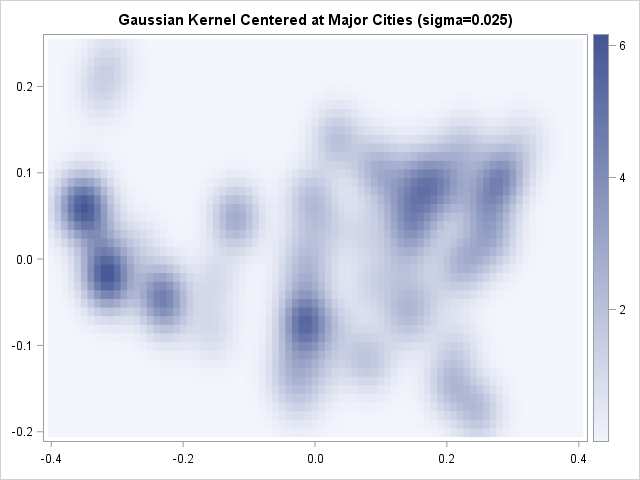
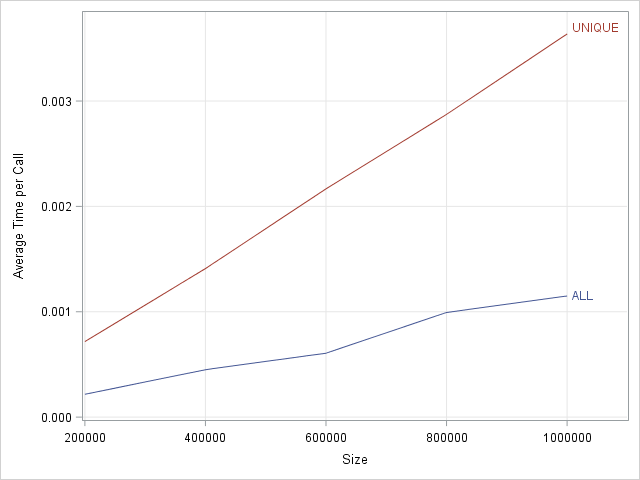
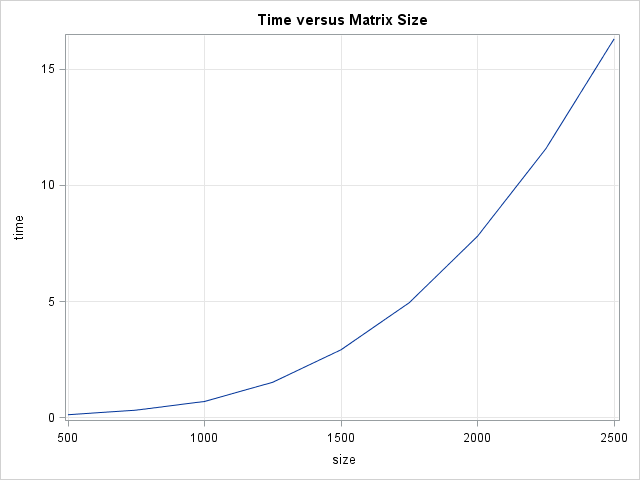
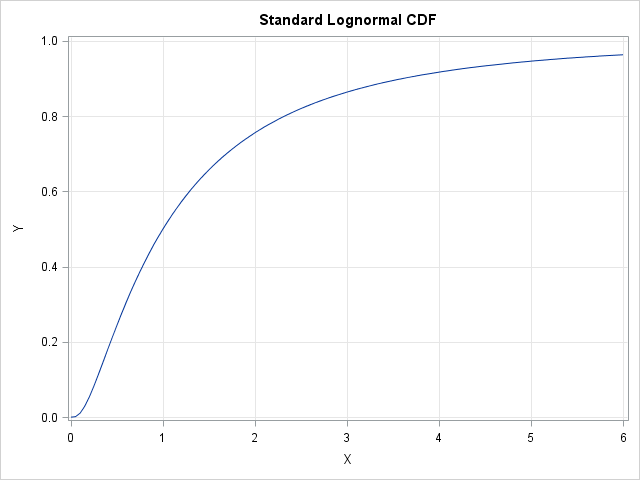
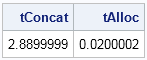
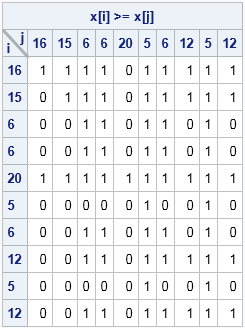
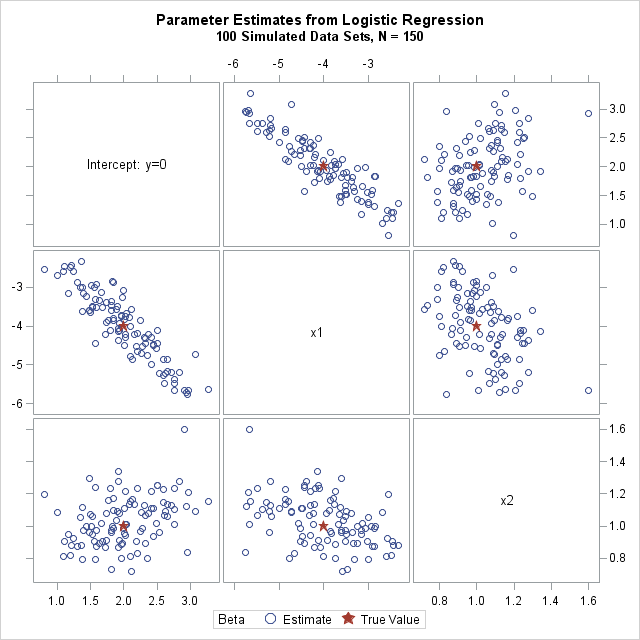
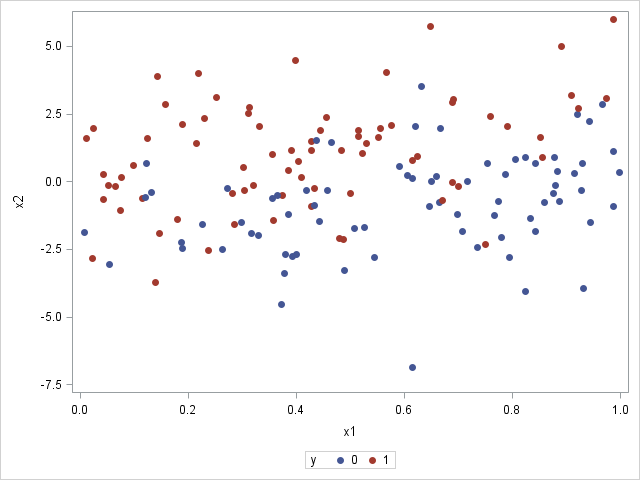
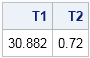
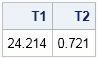
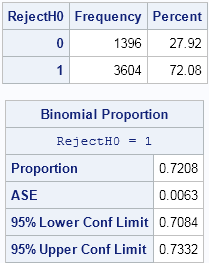
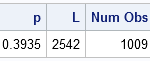
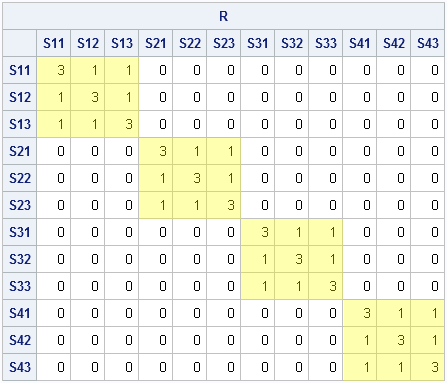
The role of Chief Operating Officer (COO) is interesting. It’s a relatively new role—and there is also relatively little consensus about the job description. In some organisations, the COO is the de facto deputy CEO. They have their fingers in most pies, from operational to strategic initiatives. In others, the
More digital channels are bringing greater connectivity and more data is bringing added complexity to organizations. All this can feel chaotic or like a fog of information warfare. As a result, the pace of disruption and data expansion require visual tools that accelerate data wrangling and modeling. To overcome complexity,
The partition problem has many variations, but recently I encountered it as an interactive puzzle on a computer. (Try a similar game yourself!) The player is presented with an old-fashioned pan-balance scale and a set of objects of different weights. The challenge is to divide (or partition) the objects into
