The April 2012 issue of ORMS Today contains a piece on "How analytics enhance the guest experience at Walt Disney World," by Pete Buczkowski and Hai Chu. While many of us are used to forecasting just one or two things (such as unit sales or revenue), Pete and Hai illustrate
I blog about a lot of topics, but the following five categories represent some of my favorite subjects. Judging by the number of readers and comments, these articles have struck a chord with SAS users. If you haven't read them, check them out. (If you HAVE read them, some are
The birthday matching problem is a classic problem in probability theory. The part of it that people tend to remember is that in a room of 23 people, there is greater than 50% chance that two people in the room share a birthday. But the birthday matching problem is also
The topic of cluster groups comes up often. By cluster group I am referring to the feature in bar charts where the group values are displayed side by side. With SAS 9.3, SG Procedures support stack or cluster grouping for Bar Charts and overlay or cluster grouping for all other
In a previous post I showed how to implement Stewart's (1980) algorithm for generating random orthogonal matrices in SAS/IML software. By using the algorithm, it is easy to generate a random matrix that contains a specified set of eigenvalues. If D = diag(λ1, ..., λp) is a diagonal matrix and
When you begin your career your most important skills are your hard, technical skills; the finance and accounting, the statistics and economics, the physics and chemistry, the engineering and calculus. But as I tell my business school mentees, as your career progresses, the emphasis changes such that much sooner than
Because I am writing a new book about simulating data in SAS, I have been doing a lot of reading and research about how to simulate various quantities. Random integers? Check! Random univariate samples? Check! Random multivariate samples? Check! Recently I've been researching how to generate random matrices. I've blogged
SAS Global Forum 2012 is right around the corner. If you will be in Orlando, too, be sure to say hello! If you have ideas for improving SAS/IML software or you would like to discuss my blog, please visit me during my hours at the SAS/IML booth in the Demo
After my post on detecting outliers in multivariate data in SAS by using the MCD method, Peter Flom commented "when there are a bunch of dimensions, every data point is an outlier" and remarked on the curse of dimensionality. What he meant is that most points in a high-dimensional cloud
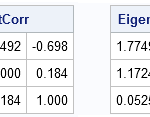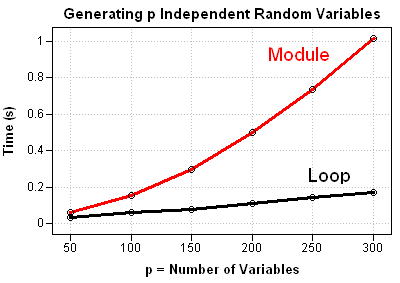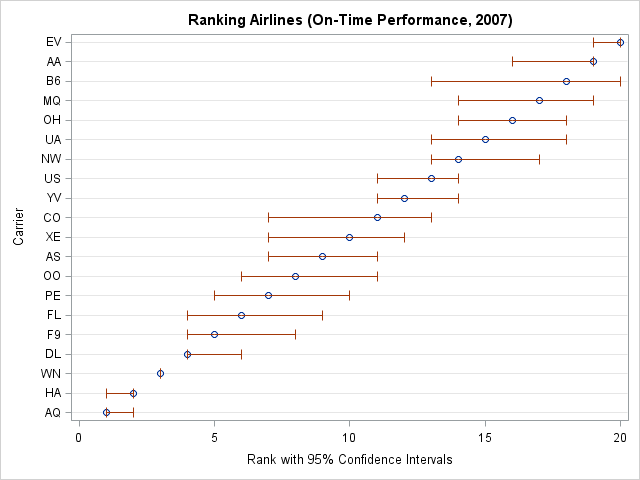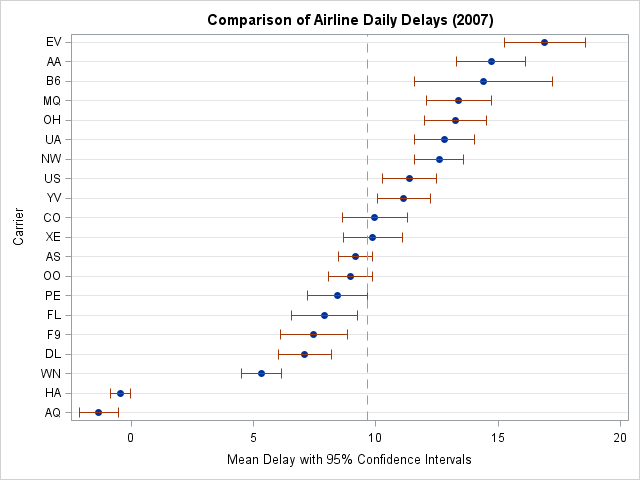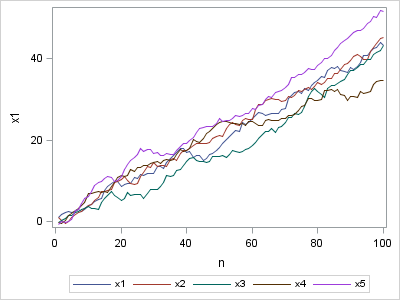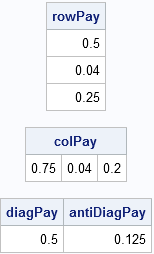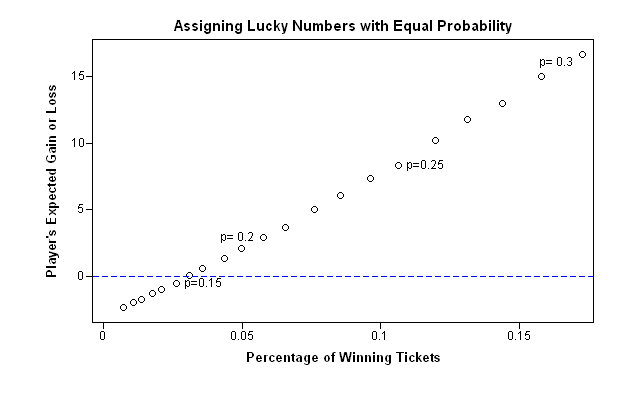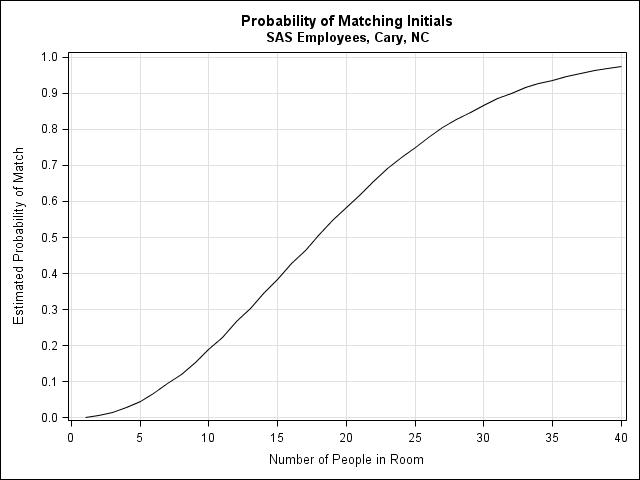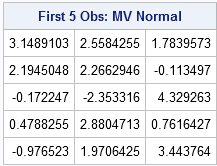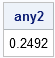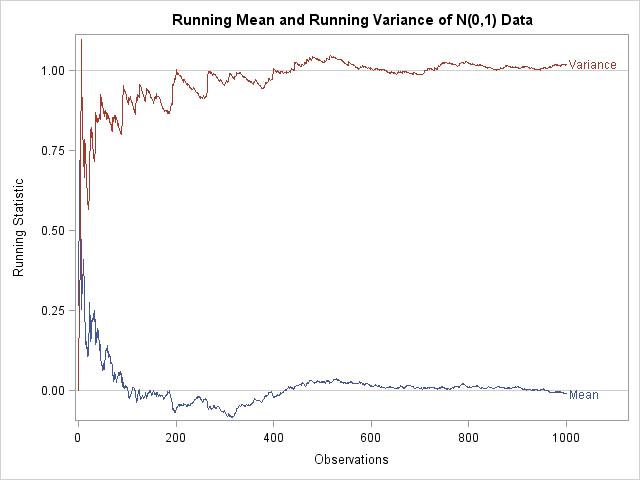
In my recent article on simulating Buffon's needle experiment, I computed the "running mean" of a series of values by using a single call to the CUSUM function in the SAS/IML language. For example, the following SAS/IML statements define a RunningMean function, generate 1,000 random normal values, and compute the
Think about what it’s like to learn to ride a bicycle, or play the piano, or hit a fast ball, or to coach a group of middle schoolers to do the same. If asked to explain how you stay balanced on a bicycle, you probably couldn’t do it. If you
It is "well known" that the pairwise deletion of missing values and the resulting computation of correlations can lead to problems in statistical computing. I have previously written about this phenomenon in my article "When is a correlation matrix not a correlation matrix." Specifically, consider the symmetric array whose elements
Hello, 2012! It's a New Year and I'm flushed with ideas for new blog articles. (You can also read about The DO Loop's most popular posts of 2011.) The fundamental purpose of my blog is to present tips and techniques for writing efficient statistical programs in SAS. I pledge to
At the beginning of 2011, I made four New Year's resolutions for my blog. As the year draws to a close, it's time to see how I did: Resolution: 100 blog posts in 2011: Completed. I blew by this goal by posting 165 articles. I recently compiled a list of
Since this is a blog about statistical programming and analysis, I am always looking for data to analyze. As 2011 ends, I look back on the 165 blog entries that I published since 01JAN2011. This article presents the 10 most popular posts, as determined by the number of people who
In simulation studies, the response variable is often a binary (or Bernoulli) variable. Often 1 is used to indicate "success" (or the occurrence of an event) whereas 0 indicates "failure" (or the absence of an event). For example, the following SAS/IML statements define a vector x of zeros and ones:
In the last year, SAS CEO Jim Goodnight and a group of R&D, Education, Sales and Marketing executives visited several universities that are in the early stages of adopting analytics within their business programs. To that effort, Goodnight addressed faculty and students at Indiana University's Kelley School of Business on
I was recently asked the following question: I am using bootstrap simulations to compute critical values for a statistical test. Suppose I have test statistic for which I want a p-value. How do I compute this? The answer to this question doesn't require knowing anything about bootstrap methods. An equivalent
“I really wish someone had shown me this function in SAS sooner, because it’s saved me a ton of time and effort,” said Brandi Rhoads as she opened her presentation at the Western Users of SAS Software (WUSS) conference in San Francisco.
Normal, Poisson, exponential—these and other "named" distributions are used daily by statisticians for modeling and analysis. There are four operations that are used often when you work with statistical distributions. In SAS software, the operations are available by using the following four functions, which are essential for every statistical programmer
Sometimes a population of individuals is modeled as a combination of subpopulations. For example, if you want to model the heights of individuals, you might first model the heights of males and females separately. The height of the population can then be modeled as a combination of the male and
NOTE: SAS stopped shipping the SAS/IML Studio interface in 2018. It is no longer supported, so this article is no longer relevant. When I write SAS/IML programs, I usually do my development in the SAS/IML Studio environment. Why? There are many reasons, but the one that I will discuss today
I've previously discussed how to find the root of a univariate function. This article describes how to find the root (zero) of a function of several variables by using Newton's method. There have been many papers, books, and dissertations written on the topic of root-finding, so why am I blogging
I recently blogged about how many times, on average, you must roll a die until you see all six faces. This question is a special case of the coupon collector's problem. My son noted that the expected value (the mean number of rolls) is not necessarily the best statistic to
"Dad? How many times do I have to roll a die until all six sides appear?" I stopped what I was doing to consider my son's question. Although I could figure out the answer mathematically, sometimes experiments are more powerful than math equations for showing how probability works. "Why don't
Tuesday's release of SAS 9.3 included the new SAS Forecast Server 4.1, which has several valuable enhancements: Combination (Ensemble) Models: A combination of forecasts using different forecasting techniques can outperform forecasts produced by using any single technique. Users can combine forecasts produced by many different models using several different combination
Welcome, SAS 9.3! I've already blogged about some interface and graphical changes that everyone should know about. Now I'll put on my statistical hat and mention a few 9.3 features that excite me, personally, as a data analyst and a statistical programmer: As a statistician, I am keen to try
As I was reviewing notes for my course "Data Simulation for Evaluating Statistical Methods in SAS," I realized that I haven't blogged about simulating categorical data in SAS. This article corrects that oversight. An Easy Way and a Harder Way SAS software makes it easy to sample from discrete "named"
My primary purpose in writing The DO Loop blog is to share what I know about statistical programming in general and about SAS programming in particular. But I also write the blog for various personal reasons, including the enjoyment of writing. The other day I encountered a concept on Ajay
In a previous blog post, I showed how you can use simulation to construct confidence intervals for ranks. This idea (from a paper by E. Marshall and D. Spiegelhalter), enables you to display a graph that compares the performance of several institutions, where "institutions" can mean schools, companies, airlines, or
