"What is the chance that two people in a room of 20 share initials?"
This was the question posed to me by a colleague who had been taking notes at a meeting with 20 people. He recorded each person's initials next to their comments and, upon editing the notes, was shocked to discover that no two people in the meeting shared initials.
Last week I analyzed the frequency distribution of initials for 4,502 SAS employees who work with me in Cary, NC. The distribution is highly skewed. For example, there are 676 possible pairs of initials (AA, AB, AC, ..., ZX, ZY, ZZ), but 212 of those combinations (31%) are not the initials of any SAS employee in Cary. Another 89 pairs (13%) are the initials of only a single person. In contrast, the most common initials, JS, are shared by 61 people.
How does this skewed distribution affect the chance that two people in the same room share initials? It makes matches more likely! Munford (TAS, 1977) showed that a uniform distribution of frequencies corresponds to the case in which it is least likely that two people in the same room share a common characteristic (such as a birthday or the same initials).
So how can you estimate the probability that two people in a room have the same initials? Use simulation!
A Simulation-Based Estimate
It works like this. Suppose you want to estimate the probability that two SAS employees in a room of 20 have a common pair of initials. You can simulate this situation in SAS/IML software as follows:
- Read the frequencies (or percentages) for each pair of initials into a SAS/IML vector. From these frequencies you can compute the empirical proportion for each pair of initials.
- Randomly select 20 initials from the vector to represent the 20 people in the room. The selections are made with a probability equal to the proportion of the initials at SAS. The program that follows uses the SampleWithReplace module from my book Statistical Programming with SAS/IML Software. (Technically, the module uses sampling with replacement, and I should use sampling without replacement because I have a finite population, but I'll ignore that small detail.)
- Count the number of unique initials in the simulated room. If the number is smaller than 20, then there is a match: at least two people have the same initials.
- Repeat the previous two steps a large number of times. The number of matches divided by the number of simulated rooms is an estimate of the probability that a random room will have a match. For example, if you generate 100,000 rooms and 58,455 of those rooms have a match, then the probability of a random room having a match is estimated by 0.58455.
The following SAS/IML program carries out this simulation:
/** program to compute the initial-matching problem **/
proc iml;
call randseed(123);
load module=SampleWithReplace;
/** read percentages for each pair of initials **/
use Sasuser.InitialFreq where(Percent>0);
read all var {Percent};
close Sasuser.InitialFreq;
p = Percent/Percent[+]; /** probability of events **/
NumRooms = 1e5; /** number of simulated rooms **/
match = j(NumRooms, 1); /** allocate results vector **/
N=20;
initials = SampleWithReplace(1:nrow(p), NumRooms||N, p);
do j = 1 to NumRooms;
u = unique(initials[j,]); /** number of unique initials **/
match[j] = N - ncol(u); /** number of common initials **/
end;
/** estimated prob of >= 1 matching initials **/
ProbEst = (match>0)[:];
print ProbEst; |
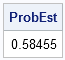
According to this simulation, if a meeting at SAS is attended by 20 employees, there is a 58% chance that two people in attendance have matching initials.
Generalizing the Problem
It is not difficult to estimate the probability that two people will have matching initials when there are N people at the meeting: just put a loop around the previous program. (You can download the SAS/IML program that carries out the simulation.)
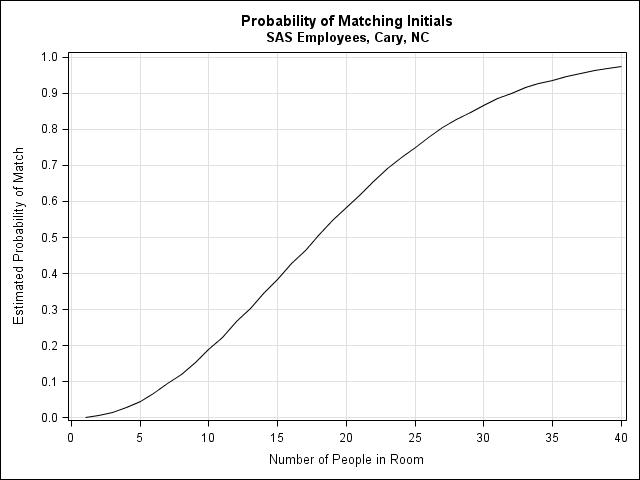
The following graph shows the probability estimates as the number of people in the room vary. The chance reaches 50% when there are 18 people in the room. Even for small meetings, the probability is not negligible: for 10 people in a room the chance is almost 20%.
Do these estimates generalize to other situations such as 20 people in a bar? Sometimes. SAS is a diverse community and so the frequency distribution I've used here might not be representative of more homogenous populations. If you record the initials of individuals in a pub in Ireland, the distributions of initials is likely to be different. (More O'Briens and McDowell's, perhaps?)
Nevertheless, I expect these estimates to apply to many situations. So next time you're stuck in a meeting, conduct a little experiment. Does anyone in the room have the same initials?

3 Comments
Pingback: Readers’ choice 2011: The DO Loop’s 10 most popular posts - The DO Loop
Pingback: Two-Letter initials: Which are the most common? - The DO Loop
Pingback: Vectorized computations and the birthday matching problem - The DO Loop