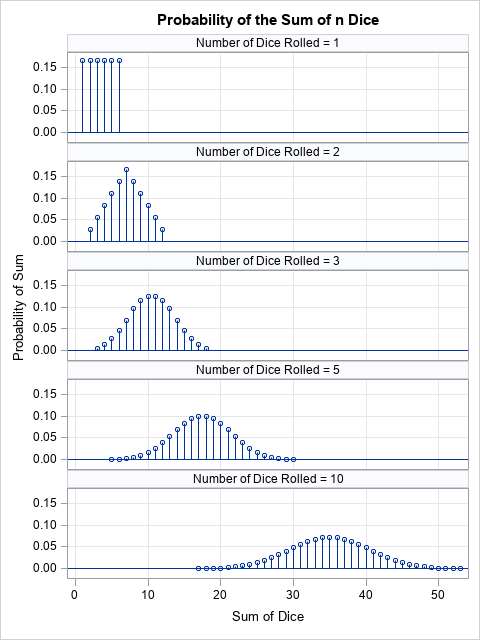
Many well-known distributions become more and more "normal looking" for large values of a parameter. Famously, the binomial distribution, Binom(p, N), can be approximated by a normal distribution when N (the sample size) is large. Similarly, the Poisson(λ) distribution is well approximated by the normal distribution when λ is large.