Ah! The joys of sets!
It is easy to test whether two vectors are equal in SAS/IML software. It is only slightly more challenging to test whether two sets are equal.
Recall that A and B are equal as sets if they contain the same elements. Order does not matter. For example, the set {1,2,3} is equal to the set {3,1,2}. Furthermore, elements can be repeated within a set, but that does not change the set. For example, the set {3,2,3,1,1} is also equal to the set {1,2,3}.
The SAS/IML language supports the following set operations:
- Union: The UNION function computes the union of sets.
- Intersection: The XSECT function computes the intersection of sets.
- Difference: The SETDIF function computes the difference between two sets.
- Subset: The ELEMENT function returns an indicator variable that specifies which elements of one vector are contained in another.
You can use any of these functions to test for the equality of sets. However, you need to call the functions twice because you need to test that A⊆B and B⊆A in order to conclude that A = B. I had several useful conversations with Ian Wakeling about the most efficient way to test sets for equality. (Thanks, Ian!) Initially, I thought that using SETDIF twice was the simplest technique: you test whether SETDIF(A,B) and SETDIF(B,A) are both empty. However, after more thought, here's the technique that I like the best:
proc iml; start SetEq(A,B); u1 = unique(A); /* unique elements in A */ u2 = unique(B); /* unique elements in B */ if ncol(u1) ^= ncol(u2) then return(0); /* number of elements differ */ return( all(u1=u2) ); /* unique elements of A = unique elements of B */ finish; |
The function compares the unique elements in the two sets. If the unique elements are the same, then the sets are equal. The function returns 1 if the sets are equal, and 0 otherwise.
You can use the following examples to test the SetEq function:
A = {1 2 3};
B = {3 1 2};
C = {3 2 3 1 1};
D = {4 1 2};
AeqB = SetEq(A,B);
AeqC = SetEq(A,C);
AeqD = SetEq(A,D);
print AeqB AeqC AeqD; |
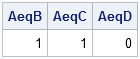
The output shows that the sets A, B, and C are equal, but the set D is not equal to the set A.
The UNIQUE function is one of my favorite SAS/IML functions. I've blogged about it many times, including using it to test whether a sequence is increasing. And, of course, the UNIQUE function is half of the UNIQUE-LOC technique for analyzing groups in the SAS/IML language.

5 Comments
Should you actually be able to make a set {3,2,3,1,1}. The definition of a set is that every element must be unique. For all purposes it stores it as {3, 2, 1} since its difference with {2} is {3, 1} and not {3, 3, 1, 1} except when you want equality. Is there a reason that set does not do the unique on itself. It seems that these are kind of a hybrid between sets and multisets, you would have to make new functions for the difference if you wanted the multiset functionality.
Sorry if I was not clear. In data analysis, the data are initially in vectors, not sets. For example, you might have a data set that contains jobs held by males and by females, and you want to compute whether the set of jobs by gender are the same, what is the intersection, what is the set difference, and so forth. Consequently, the functions I mention operate on vectors, not sets. The UNIQUE function returns the mathematical set, so if I want to use "pure" sets, I can convert the vector of data to a set. However, sometimes it is more useful to work directly with the vectors so that you can discover how many "female construction workers" and how many "male nurses" there are in the data set.
Dear Rick
I am your loyal reader and read your blogs regularly. I benefited a lot from your blog and really appreciate your sharing.
I recently encountered one wierd problem. I found I cannot call one macro in another macro repeatedly. In my macro A, I have do loop, "%do i=1 %to &fcount" with "%end". In this do loop, I try to call another macro B. However, I found as long as I call macro B, the B job was done for this cycle, but then the macro A stopped. Anything after macro B in the macro A was not executed. And the following do loop was not executed.(no loop at all).
I used another method "%sysfunc(getvarc)" and the macro B was not executed in the do loop created by using the %sysfunc method.
I got really lost. I wrote programs using macro for many times, and this is the first time I use %do--%end loop and got failed. Could you tell me what mistake I made?
If you need my program, I can show you.
Thanks!
Vivian
There is a great resource for questions like this: the SAS community forums! https://communities.sas.com/community/support-communities
Pingback: Finding elements in one vector that are not in another vector - The DO Loop