If you use a word three times, it's yours.
-Unknown
When I was a child, my mother used to encourage me to increase my vocabulary by saying, "If you use a word three times, it's yours for life." I believe that the same saying holds for programming techniques: Use a technique three times, and it sticks with you.
I've blogged before about various ways to fill or extract portions of a matrix. I recently used the ROW/COL technique for the third time, and I suspect I will use it more in the future. The technique (which is explained in a previous post) uses two helper functions, ROW and COL, to fill and extract certain elements in a matrix, such as the upper or lower triangular elements. The ROW and COL functions are new in SAS/IML 13.1, which is shipped with SAS 9.4m1. For example, the following statements fill the lower triangular portion of a matrix with random variates from a standard normal distribution:
proc iml; /* Prior to SAS/IML 13.1, define helper functions ROW and COL. These functions are built-ins for SAS/IML 13.1 and later. */ start row(x); /* return matrix m such that m[i,j] = i */ return( repeat( T(1:nrow(x)), 1, ncol(x) )); finish; start col(x); /* return matrix m such that m[i,j] = j */ return( repeat(1:ncol(x), nrow(x)) ); finish; p = 5; /* specify dimensions */ x = j(p, p, 0); /* allocate p x p matrix of zeros */ r = row(x); /* create helper matrices */ c = col(x); /* fill lower triangle with normal variates */ lowerIdx = loc(r > c); call randseed(12345); y = j(1, ncol(lowerIdx)); /* allocate vector with correct number of elements */ call randgen(y, "Normal"); /* fill it with random variates */ x[lowerIdx] = y; /* assign values to lower triangular matrix */ print x; |
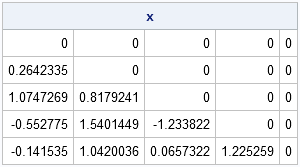
Filling the lower-triangular portion of a matrix with random numbers is not just an example that demonstrates this technique, it is also the first step in the simulation of variates from a Wishart distribution.
You can use the r and c matrices to define the indices for other portions of a matrix. For example:
- The upper triangular portion of a matrix: r < c
- the diagonal: r = c
- the anti-diagonal: r + c -1 = p
- the super- and subdiagonals, and so forth.
Try it out. And if you use it three times, it's yours for life!

1 Comment
Pingback: A Christmas tree matrix - The DO Loop