I previously wrote an article about the Lambert W function. The Lambert W function is the inverse of the function g(x) = x exp(x). This means that you can use it to find the value of x such that g(x)=c for any value of c in the range of g, which
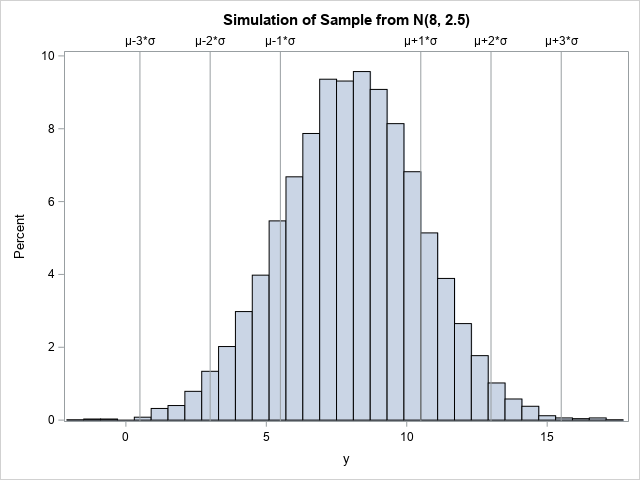
They say nothing in life is certain other than death and taxes, but there something else I’ve found I can count on from experience: sending out invites for a party on social media only to receive a few affirmative responses and a whole slew of “maybe”. I know my friends
A remarkable result in probability theory is the "three-sigma rule," which is a generic name for theorems that bound the probability that a univariate random variable will appear near the center of its distribution. This article discusses the familiar three-sigma rule for the normal distribution, a less-familiar rule for unimodal
