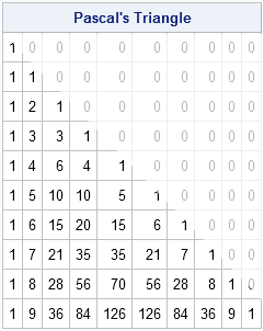
Pascal's triangle is the name given to the triangular array of binomial coefficients. The nth row is the set of coefficients in the expansion of the binomial expression (1 + x)n. Complicated stuff, right?
Well, yes and no. Pascal's triangle is known to many school children who have never heard of polynomials or coefficients because there is a fun way to construct it by using simple addition. You start by writing down the number 1. The second line is the sum of the first line and the result of shifting the first line one column to the right. This process continues: to form a new row of the triangle, add the previous row to a right-shifted copy of the previous row. To make the bookkeeping work out, you pretend that missing items are zero, as shown by the ghostly images of zeros in the image at the top of this article.
In math terms, you can find the kth element of the nth row, by adding the (k–1)th and the kth elements of the previous row. This geometric construction is a result of the following recursive relationship between binomial coefficients:
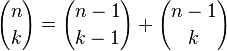
Recently several participants on the SAS/IML Support Community posted programs that created Pascal's triangle by using the COMB function in SAS software. This article shows how to create Pascal's triangle and how self-similar (fractal) patterns arise when you visualize the triangle in certain ways.
Creating an array of binomial coefficients
The simplest way to create Pascal's matrix is to use the COMB function to generate the values of the binomial coefficients. You can start with a matrix that contains all zeros. The first k elements of the kth row are filled with binomial coefficients. You can do this in the SAS DATA step, or in the SAS/IML language as follows:
proc iml;
start PascalTriangle(n);
m = j(n,n,0); /* matrix with all zeros */
do k = 1 to n; /* for the kth row... */
m[k,1:k] = comb(k-1, 0:k-1); /* fill nonzero elements */
end;
return(m);
finish;
T10 = PascalTriangle(10);
print T10[F=3. L="Pascal's Triangle, Level 10" r=("n=0":"n=9")]; |
The resulting matrix is similar to the image at the top of this post, with the upper triangular elements equal to zero. Notice that the SAS/IML language enables you to pass in a vector argument to a Base SAS function. In this case, a vector (0:k-1) is passed to the COMB function and the resulting row vector overwrites some of the zeros in the matrix m.
Using the previous row to create the next row of Pascal's matrix
You can also create Pascal's matrix by using the "schoolchild method" of adding adjacent elements from the previous row to create the new row. The construction is similar to the way that you can construct cellular automata. The following SAS/IML module constructs Pascal's triangle by using addition; no need to call the COMB function!
start PascalRule(n);
m = j(n,n,0); /* initialize with zeros */
m[,1] = 1; /* set first column to 1 */
j = 2:n; /* elements to compute */
do k = 2 to n;
/* for kth row, add adjacent elements from previous row */
m[k,j] = m[k-1,j-1] + m[k-1,j];
end;
return(m);
finish;
T10 = PascalRule(10);
print T10[F=3. L="Pascal's Triangle, Level 10" r=("n=0":"n=9")]; |
Self-similar structures in Pascal's triangle
At first glance, the numbers in Pascal triangle have a simple structure. The edges of the triangle are all 1. The interior values increase geometrically, reaching their maximum values in the middle of the final row. However, if you label each value according to whether it is odd or even, a surprising pattern reveals itself!
The following SAS/IML program creates a Pascal matrix with 56 rows. The upper-triangular elements are set to missing values. The program then creates a discrete heat map that shows the parity (even or odd) of the remaining elements. Even numbers are displayed as white squares; odd numbers are displayed as black squares.ods graphics / width=400px height=380px;
m = PascalRule(56);
m[ loc(col(m)>row(m)) ] = .; /* replace zeros with missing values */
mod2 = mod(m,2);
call heatmapdisc(mod2) colorramp={WHITE BLACK}
displayoutlines=0 title="Pascal's Triangle mod 2"; |
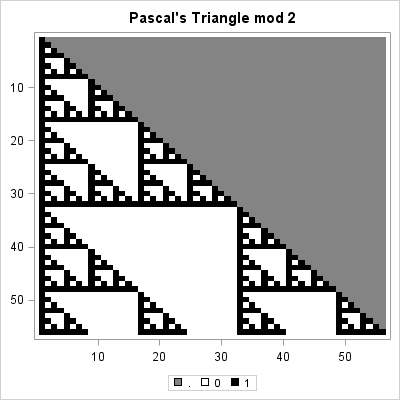
The resulting heat map bears a striking resemblance to the fractal known as Sierpinski's triangle. This fact is not widely known, but the image is comprehensible to school-age children. However, few children have the patience and stamina to color hundreds of cells, so using software to color the triangle is definitely recommended!
The fascinating self-similar pattern might inspire you to wonder what happens if the elements are colored according to some other scheme. For example, what is the pattern if you divide the elements of Pascal's triangle by 3 and visualize the remainders? Or division by 4? Or 5? The following loop creates three heat maps that visualize the numbers in Pascal's triangle modulo k, where k = 3, 4, and 5.
do k = 3 to 5;
mod = mod(m,k);
ramp = palette("greys", k);
title = "Pascal's Triangle mod " + char(k,1);
call heatmapdisc(mod) colorramp=ramp displayoutlines=0 title=title;
end; |
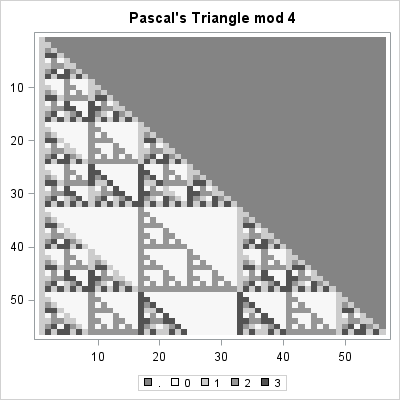
The "mod 4" result is shown. The other heat maps are similar. Each shows a self-similar pattern. One of the surprising results of chaos theory and fractals is that these complicated self-similar structures can arise from simple iterative arithmetic operations (adding adjacent elements) followed by a modular operation.
Creating larger triangles
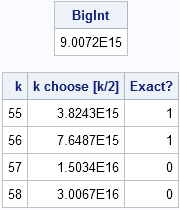
The astute reader will have noticed that 56 rows is a curious number. Why not 64 rows? Or 100? The answer is that the modular operations require that the numbers in Pascal's triangle be exactly representable as an integer. Although you can compute more than 1,000 rows of Pascal's triangle in double precision, at some point the numbers grow so large that they can no longer be represented exactly with an 8-byte integer.
You can use the SAS CONSTANT function to find the largest integer, B, such that smaller integers (in magnitude) are exactly represented by an 8-byte numeric value. It turns out that the largest value in a Pascal triangle with k rows is "k choose floor(k/2)," and this value exceeds B when k=57, as shown by the following statements. Thus the modulo operations will become inaccurate for k>56.
B = constant('ExactInt');
print B;
k = T(55:58);
c = comb(k, floor(k/2));
print k c[L="k choose [k/2]"] (c<B)[L="Exact?"]; |
I think Pascal's triangle is very cool. When did you first encountered Pascal's triangle? Were you fascinated or bored? Share your story in the comments.

6 Comments
Very nice article! It might not be visually pleasing like your heatmaps above, but there are interesting number sequences to found in the sums of the anti-diagonals of the Pascal Matrix and other matrices derived from it. Using a small function to find the sums of the first n anti-diagonals of a square matrix:
.
start AntiDiagSum( x );
n = nrow( x );
s = sparse( x );
s[ , 2] = s[ , 2] + s[ , 3] - 1;
return( full( s , 2#n - 1, n )[1:n , +] );
finish;
.
The following can all be derived:
.
print 'Fibonacci Numbers', (AntiDiagSum( PascalTriangle(12) ) );
print 'NegaFibonacci Numbers', (AntiDiagSum( inv( PascalTriangle(12) ) ) );
print 'Pell Numbers', (AntiDiagSum( PascalTriangle(12)**2 ) );
The following quantities reveal some other nice patterns:
1. The sum of elements in each row.
2. The alternating sum of elements in each row.
3. The sum of squares of elements in each row.
All three patterns have nice combinatorial proofs.
Pingback: A matrix computation on Pascal’s triangle - The DO Loop
Pingback: Self-similar structures from Kronecker products - The DO Loop
Thank you so much for your post! I have been fascinated by Pascal's triangle since learning about it in school when I was young. Beyond its connection to binomial coefficients and Sierpinski's triangle (which you mention), I think it's unbelievable how many other patterns emerge (related to triangular numbers, pyramidal numbers, Fibonacci's sequence, Catalan numbers, etc.). I have only recently seen how computer scientists are using code to explore the array, so I really appreciate the post. I actually just published a novel that uses Pascal's triangle as a structural framework. It's called The Right Amount of Brilliance and it's available here in Kindle and paperback formats: https://www.amazon.com/dp/B08F9FK9BP. I figured I'd post about the book in case it appeals to other people who find the triangle interesting.
how to make
1
22
333
4444
5555